General linear models


\[ Residual_i = y_i - E(Y_i) \]


\[\underbrace{E(Y)}_{Link~~function} = \underbrace{\beta_0 + \beta_1x_1~+~...~+~\beta_px_p}_{Systematic} + \varepsilon, ~~\varepsilon\sim Dist(...)\]
\[\underbrace{E(Y)}_{Link~~function} = \underbrace{\beta_0 + \beta_1x_1~+~...~+~\beta_px_p}_{Systematic}~~\underbrace{~+~e}_{Random}\]
\[\underbrace{g(\mu)}_{Link~~function} = \underbrace{\beta_0 + \beta_1x_1~+~...~+~\beta_px_p}_{Systematic}~~\underbrace{~+~e}_{Random}\]
| Response variable | Probability distribution | Link function | Model name |
|---|---|---|---|
| Continuous measurements | Gaussian |
identity: \(\mu\) | Linear regression |
| Binary | Binomial |
logit: \(log\left(\frac{\pi}{1-\pi}\right)\) | Logistic regression |
|
probit: \(\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\alpha+\beta.X} exp\left(-\frac{1}{2}Z^2\right)dZ\) | Probit regression | ||
|
Complimentary log-log: \(log(-log(1-\pi))\) | Logistic regression | ||
| Counts | Poisson |
log: \(log \mu\) |
Poisson regression log-linear model |
| Negative binomial | \(log\left(\frac{\mu}{\mu+\theta}\right)\) | Negative biomial regression | |
| Quasi-poisson | \(log\mu\) | Poisson regression |
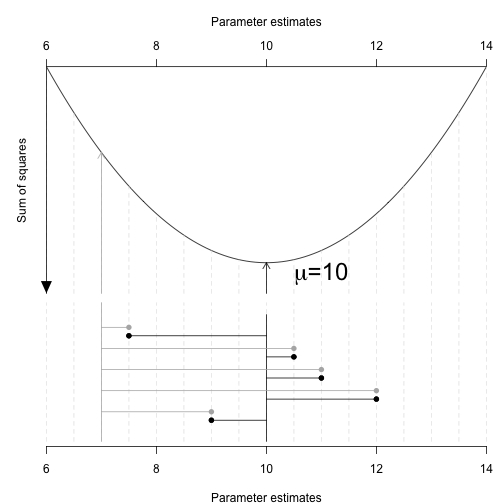
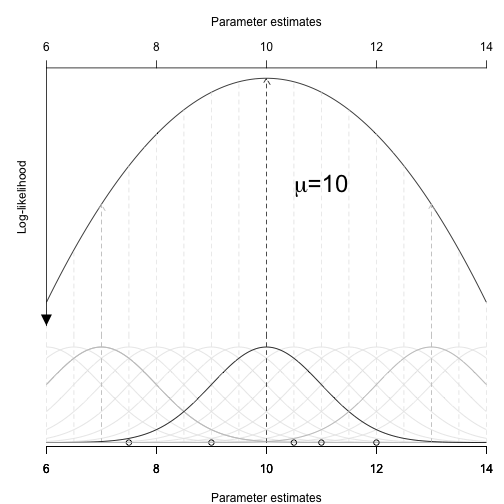
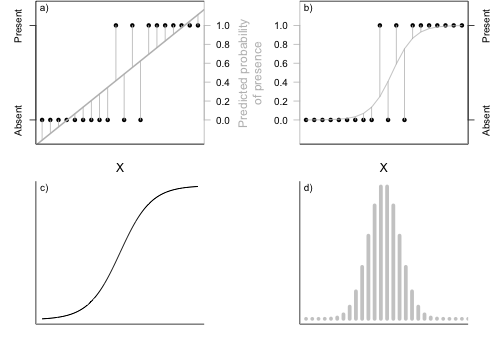
Link: \(log\left(\frac{\pi}{1-\pi}\right)\)
Transform scale of linear predictor (\(-\infty,\infty\)) into that of the response (0,1)
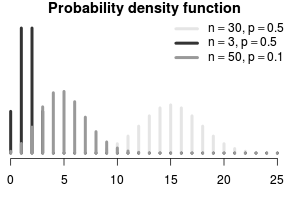
\[E(Y) = \left(\begin{array}{c} n\\x \end{array}\right)p^{x}(1-p)^{n-x}\]
Spread assumed to be equal to mean. (\(\phi = 1\))
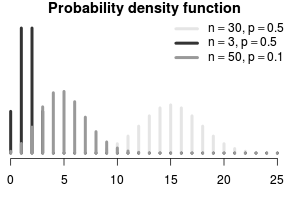
Sample more varied than expected from its mean
dat.glmL <- glm(y ~ x, data = dat, family = "binomial")dat.glmL <- glm(y ~ x, data = dat, family = "binomial")plot(dat.glmL)dat.glmL <- glm(y ~ x, data = dat, family = "binomial")plot(dat.glmL)r summary(data.glmL} Slope parameter is on log odds-ratio scale
r summary(data.glmL} Slope parameter is on log odds-ratio scale
polis <- read.csv('../data/polis.csv', strip.white=T)
head(polis) ISLAND RATIO PA
1 Bota 15.41 1
2 Cabeza 5.63 1
3 Cerraja 25.92 1
4 Coronadito 15.17 0
5 Flecha 13.04 1
6 Gemelose 18.85 0ggplot(polis, aes(y=PA, x=RATIO))+geom_point()+
geom_smooth(method='glm', formula=y~x, family='binomial')Error: could not find function "ggplot"plot(PA~RATIO, data=polis )
abline(lm(PA~RATIO, data=polis))
with(polis,lines(lowess(PA~RATIO)))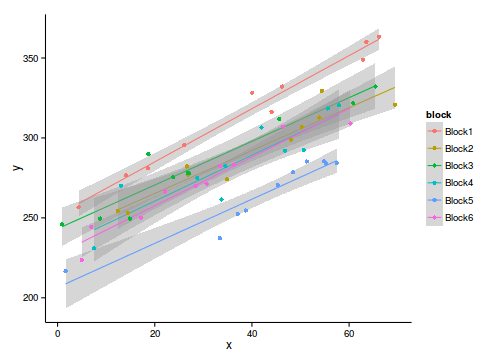
polis.glm <- glm(PA ~ RATIO, family=binomial, data=polis)
par(mfrow=c(2,3))
plot(polis.glm)
##Check the model for lack of fit via:
##Pearson chisq
polis.resid <- sum(resid(polis.glm, type="pearson")^2)
1-pchisq(polis.resid, polis.glm$df.resid)[1] 0.5715#No evidence of a lack of fit
#Deviance
1-pchisq(polis.glm$deviance, polis.glm$df.resid)[1] 0.6514#No evidence of a lack of fit
#Estimate dispersal
polis.resid/polis.glm$df.resid[1] 0.9019#OR
polis.glm$deviance/polis.glm$df.resid[1] 0.8365#Number of zeros
polis.tab<-table(polis$PA==0)
polis.tab/sum(polis.tab)
FALSE TRUE
0.5263 0.4737 summary(polis.glm)
Call:
glm(formula = PA ~ RATIO, family = binomial, data = polis)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.607 -0.638 0.237 0.433 2.099
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.606 1.695 2.13 0.033
RATIO -0.220 0.101 -2.18 0.029
(Intercept) *
RATIO *
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 26.287 on 18 degrees of freedom
Residual deviance: 14.221 on 17 degrees of freedom
AIC: 18.22
Number of Fisher Scoring iterations: 6exp(-0.296)[1] 0.7438#R2
1-(polis.glm$deviance/polis.glm$null)[1] 0.459anova(polis.glm, test='Chisq')Analysis of Deviance Table
Model: binomial, link: logit
Response: PA
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 18 26.3
RATIO 1 12.1 17 14.2 0.00051
NULL
RATIO ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1par(mar=c(4,5,0,0))
plot(PA~RATIO, data=polis,type="n",ann=F,axes=F)
points(PA~RATIO, data=polis,pch=16)
xs <- seq(min(polis$RATIO),max(polis$RATIO),len=1000)
ys <- predict(polis.glm,newdata=data.frame(RATIO=xs),
type='link',se=T)
ys$lwr <- polis.glm$family$linkinv(ys$fit - 2*ys$se.fit)
ys$upr <- polis.glm$family$linkinv(ys$fit + 2*ys$se.fit)
ys$fit <- polis.glm$family$linkinv(ys$fit)
lines(ys$fit~xs, col='black')
lines(ys$lwr~xs, col='black',lty=2)
lines(ys$upr~xs, col='black',lty=2)
axis(1)
mtext("Island perimeter to area ratio",1,cex=1.5,line=3)
axis(2,las=2)
mtext(expression(paste(italic(Uta)," lizard presence/absence")),2,cex=1.5,line=3)
box(bty="l")
#LD50
ld50<--polis.glm$coef[1]/polis.glm$coef[2]
newdata <- data.frame(RATIO=xs, fit=ys$fit, lower=ys$lwr, upper=ys$upr)
ggplot(newdata, aes(y=fit, x=RATIO))+geom_line()+
geom_ribbon(aes(ymin=lower, ymax=upper), fill='blue',alpha=0.2)+
geom_point(data=polis, aes(y=PA, x=RATIO))Error: could not find function "ggplot"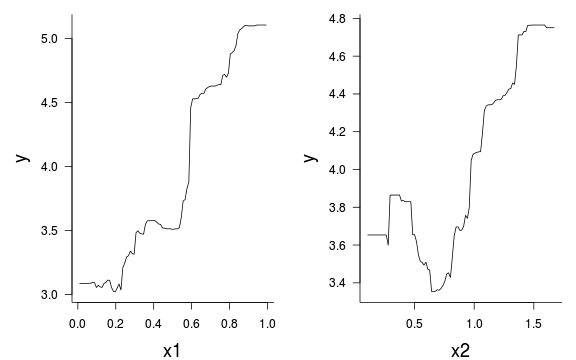
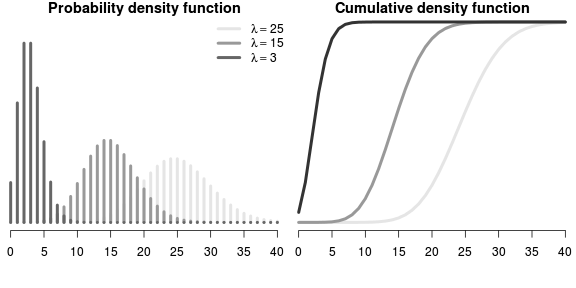
\[ p(Y_i) = \frac{e^{-\lambda}\lambda^x}{x!} \]
\[log(\mu)=\beta_0+\beta_1x_i+...+\beta_px_p\]
Spread assumed to be equal to mean. (\(\phi = 1\))

Sample more varied than expected from its mean
data.pois <- read.csv('../data/data.pois.csv', strip.white=T)
head(data.pois) y x
1 1 1.025
2 2 2.697
3 3 3.626
4 2 4.949
5 4 6.025
6 8 6.254library(car)
scatterplot(y~x,data=data.pois)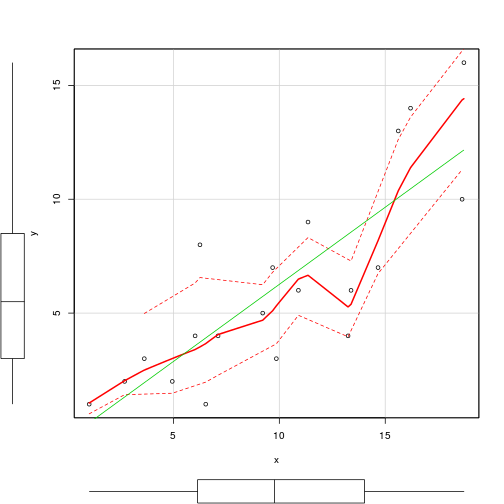
scatterplot(y~x,data=data.pois, log='y')
rug(jitter(data.pois$y), side=2)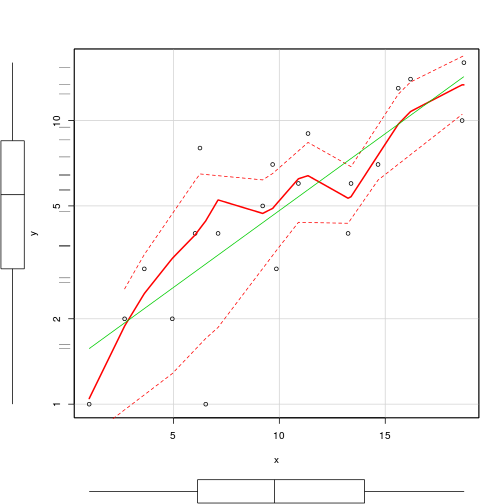
hist(data.pois$y)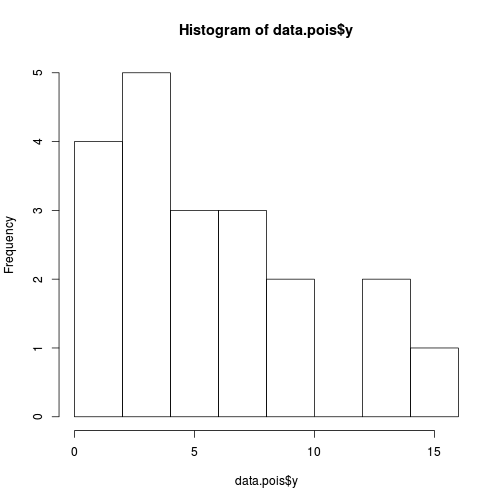
boxplot(data.pois$y, horizontal=TRUE)
rug(jitter(data.pois$y), side=1)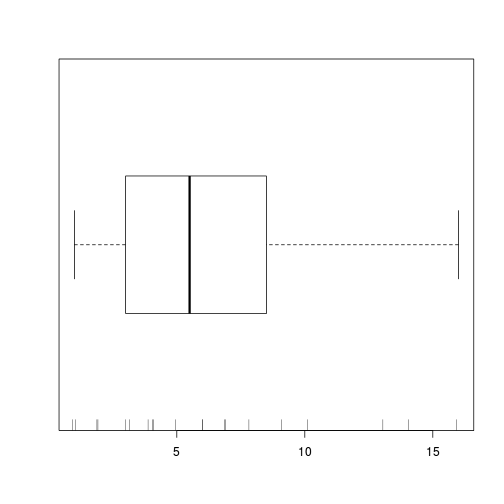
#plot(y~x, data.pois, log="y")
#with(data.pois, lines(lowess(y~x)))
#library(car)
#scatterplot(y~x,data=data.pois, log='y')
#rug(jitter(data.pois$y), side=2)
#Zero inflation
#proportion of 0's in the data
data.pois.tab<-table(data.pois$y==0)
data.pois.tab/sum(data.pois.tab)
FALSE
1 #proportion of 0's expected from a Poisson distribution
mu <- mean(data.pois$y)
cnts <- rpois(1000, mu)
data.pois.tab <- table(cnts == 0)
data.pois.tab/sum(data.pois.tab)
FALSE TRUE
0.999 0.001 #fit model
data.pois.glm <- glm(y~x, data=data.pois, family="poisson")
data.pois.glm <- glm(y~x, data=data.pois, family=poisson(link='log'))
#Model validation
par(mfrow=c(2,3))
plot(data.pois.glm, ask=F, which=1:6)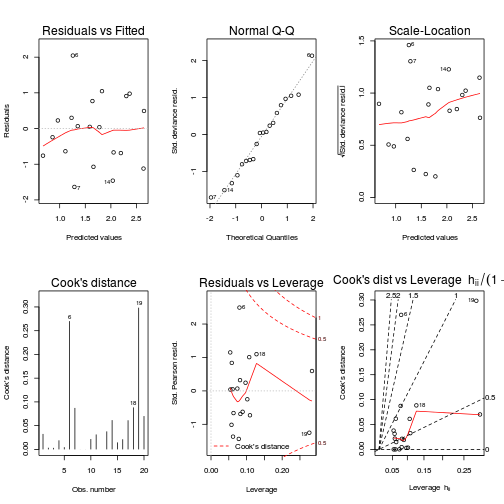
#goodness of fit
data.pois.resid <- sum(resid(data.pois.glm, type = "pearson")^2)
1 - pchisq(data.pois.resid, data.pois.glm$df.resid)[1] 0.4897#Deviance based
1-pchisq(data.pois.glm$deviance, data.pois.glm$df.resid)[1] 0.5076data.pois.glmG <- glm(y~x, data=data.pois, family="gaussian")
library(MuMIn)
AICc(data.pois.glm, data.pois.glmG) df AICc
data.pois.glm 2 91.02
data.pois.glmG 3 99.78#Poisson deviance
data.pois.glm$deviance[1] 17.23#Gaussian deviance
data.pois.glmG$deviance[1] 118.1data.pois.resid/data.pois.glm$df.resid[1] 0.9717data.pois.glm$deviance/data.pois.glm$df.resid[1] 0.957#Or alternatively, via Pearson's residuals
Resid <- resid(data.pois.glm, type = "pearson")
sum(Resid^2) / (nrow(data.pois) - length(coef(data.pois.glm)))[1] 0.9717summary(data.pois.glm)
Call:
glm(formula = y ~ x, family = poisson(link = "log"), data = data.pois)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.635 -0.705 0.044 0.562 2.046
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.5600 0.2539 2.21 0.027
x 0.1115 0.0186 6.00 2e-09
(Intercept) *
x ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 55.614 on 19 degrees of freedom
Residual deviance: 17.226 on 18 degrees of freedom
AIC: 90.32
Number of Fisher Scoring iterations: 4library(gmodels)
ci(data.pois.glm) Estimate CI lower CI upper Std. Error
(Intercept) 0.5600 0.02649 1.0935 0.25395
x 0.1115 0.07247 0.1506 0.01858
p-value
(Intercept) 2.744e-02
x 1.971e-091-(data.pois.glm$deviance/data.pois.glm$null)[1] 0.6903par(mfrow=c(1,1), mar = c(4, 5, 0, 0))
plot(y ~ x, data = data.pois, type = "n", ann = F, axes = F)
points(y ~ x, data = data.pois, pch = 16)
xs <- seq(min(data.pois$x), max(data.pois$x), len = 1000)
#ys <- predict(data.pois.glm, newdata = data.frame(x = xs), type = "response", se = T)
ys <- predict(data.pois.glm, newdata = data.frame(x = xs), type = "link", se = T)
ys$lwr <- exp(ys$fit - 2*ys$se.fit)
ys$upr <- exp(ys$fit + 2*ys$se.fit)
ys$fit <- exp(ys$fit)
lines(ys$fit ~ xs, col = "black")
lines(ys$lwr ~ xs, col = "black", lty = 2)
lines(ys$upr ~ xs, col = "black", lty = 2)
polygon(c(xs,rev(xs)), c(ys$lwr,rev(ys$upr)), border=NA, col="#0000FF50")
#lines(ys$fit - 2 * ys$se.fit ~ xs, col = "black", type = "l", lty = 2)
#lines(ys$fit + 2 * ys$se.fit ~ xs, col = "black", type = "l", lty = 2)
axis(1)
mtext("X", 1, cex = 1.5, line = 3)
axis(2, las = 2)
mtext("Abundance of Y", 2, cex = 1.5, line = 3)
box(bty = "l")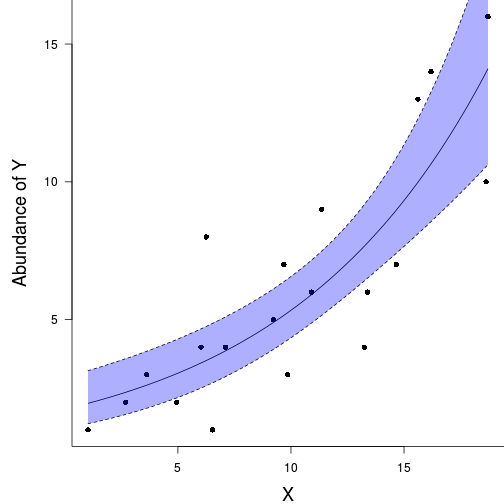
data.qp <- read.table('../data/data.qp.csv', header=T, sep=',', strip.white=T)
head(data.qp) y x
1 0 1.025
2 3 2.697
3 0 3.626
4 5 4.949
5 6 6.025
6 1 6.254ggplot(data.qp, aes(y=y, x=x))+geom_point()+geom_rug()+
geom_smooth(method='lm')Error: could not find function "ggplot"## library(car)
## scatterplot(y~x,data=data.qp)
## scatterplot(y~x,data=data.qp, log='y')
plot(y~x, data.qp)
with(data.qp, lines(lowess(y~x)))
rug(jitter(data.qp$y), side=2)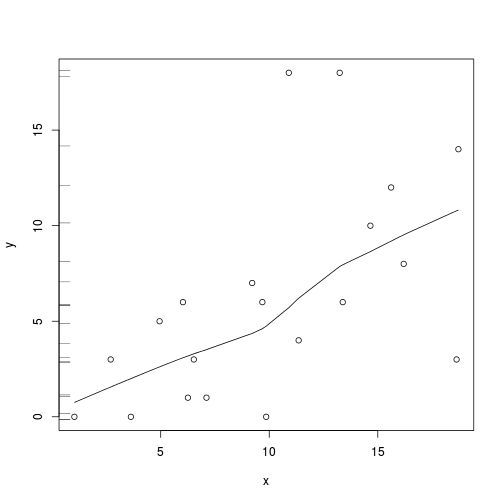
plot(y~x, data.qp, log="y")
with(data.qp, lines(lowess(y~x)))
rug(jitter(data.qp$y), side=2)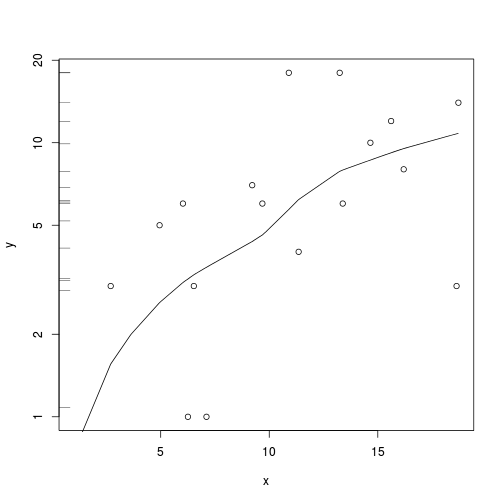
hist(data.qp$y)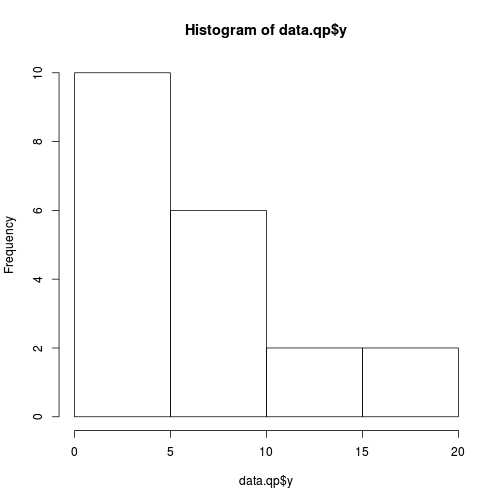
boxplot(data.qp$y, horizontal=TRUE)
rug(jitter(data.qp$y), side=1)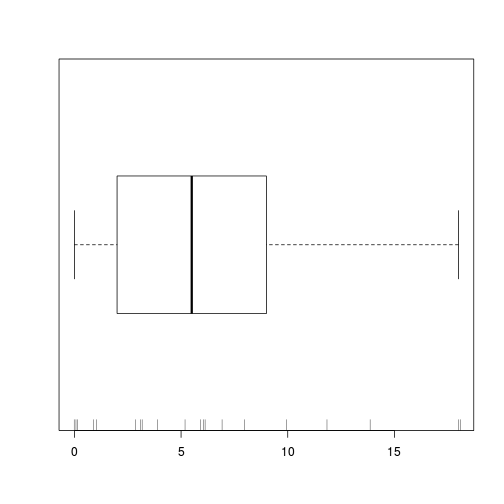
#Zero inflation
#proportion of 0's in the data
data.qp.tab<-table(data.qp$y==0)
data.qp.tab/sum(data.qp.tab)
FALSE TRUE
0.85 0.15 #proportion of 0's expected from a Poisson distribution
mu <- mean(data.qp$y)
cnts <- rpois(1000, mu)
data.qp.tab <- table(cnts == 0)
data.qp.tab/sum(data.qp.tab)
FALSE
1 #fit model
data.qp.glm<-glm(y~x, data=data.qp, family="poisson")
data.qp.glm2 <- glm(y~x, data=data.qp, family="quasipoisson")
AICc(data.qp.glm, data.qp.glm2) df AICc
data.qp.glm 2 135.6
data.qp.glm2 2 NAanova(data.qp.glm, data.qp.glm2, test='Chisq')Analysis of Deviance Table
Model 1: y ~ x
Model 2: y ~ x
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 18 70
2 18 70 0 0 #Model validation
par(mfrow=c(2,3))
plot(data.qp.glm, ask=F, which=1:6)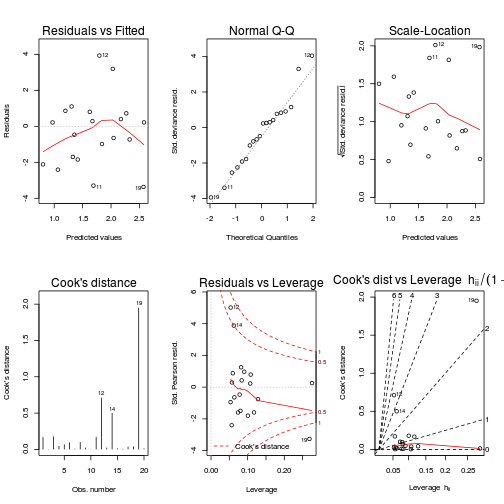
data.qp.glm$deviance/data.qp.glm$df.resid[1] 3.888#Or alternatively, via Pearson's residuals
Resid <- resid(data.qp.glm, type = "pearson")
sum(Resid^2) / (nrow(data.qp) - length(coef(data.qp.glm)))[1] 3.699summary(data.qp.glm)
Call:
glm(formula = y ~ x, family = "poisson", data = data.qp)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.366 -1.736 -0.124 0.744 3.933
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.6997 0.2468 2.84 0.0046
x 0.1005 0.0184 5.47 4.4e-08
(Intercept) **
x ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 101.521 on 19 degrees of freedom
Residual deviance: 69.987 on 18 degrees of freedom
AIC: 134.9
Number of Fisher Scoring iterations: 5library(gmodels)
ci(data.qp.glm) Estimate CI lower CI upper Std. Error
(Intercept) 0.6997 0.18121 1.218 0.24677
x 0.1005 0.06192 0.139 0.01835
p-value
(Intercept) 4.579e-03
x 4.389e-081-(data.qp.glm$deviance/data.qp.glm$null)[1] 0.3106par(mar = c(4, 5, 0, 0))
plot(y ~ x, data = data.qp, type = "n", ann = F, axes = F)
points(y ~ x, data = data.qp, pch = 16)
xs <- seq(0, 20, l = 1000)
ys <- predict(data.pois.glm, newdata = data.frame(x = xs), type = "link", se = T)
ys$lwr <- exp(ys$fit - 2*ys$se.fit)
ys$upr <- exp(ys$fit + 2*ys$se.fit)
ys$fit <- exp(ys$fit)
lines(ys$fit ~ xs, col = "black")
lines(ys$lwr ~ xs, col = "black", lty = 2)
lines(ys$upr ~ xs, col = "black", lty = 2)
axis(1)
mtext("X", 1, cex = 1.5, line = 3)
axis(2, las = 2)
mtext("Abundance of Y", 2, cex = 1.5, line = 3)
box(bty = "l")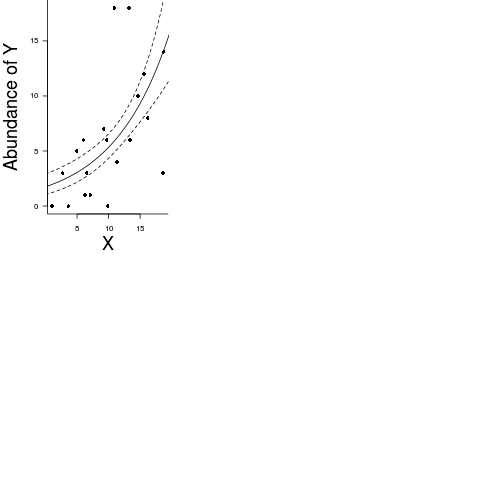
\[p(y_i)=\frac{\Gamma(y_i+\omega)}{\Gamma(\omega)y!}\times\frac{\mu_i^{y_i}\omega^\omega}{(\mu_i+\omega)^{\mu_i+\omega}}\]
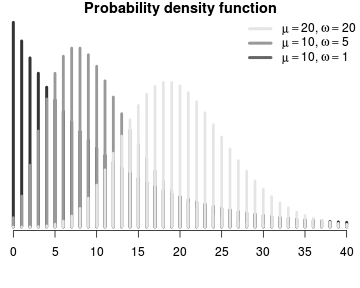
\[p(y_i)=\frac{\Gamma(y_i+\omega)}{\Gamma(\omega)y!}\times\frac{\mu_i^{y_i}\omega^\omega}{(\mu_i+\omega)^{\mu_i+\omega}}\]
data.nb <- read.table('../data/data.nb.csv', header=T, sep=',', strip.white=T)
head(data.nb) y x
1 1 1.042
2 7 2.498
3 2 3.677
4 4 3.798
5 1 4.871
6 9 7.690scatterplot(y~x, data.nb, log='y')Error: NA/NaN/Inf in 'y'
plot(y~x, data.nb)
with(data.nb, lines(lowess(y~x)))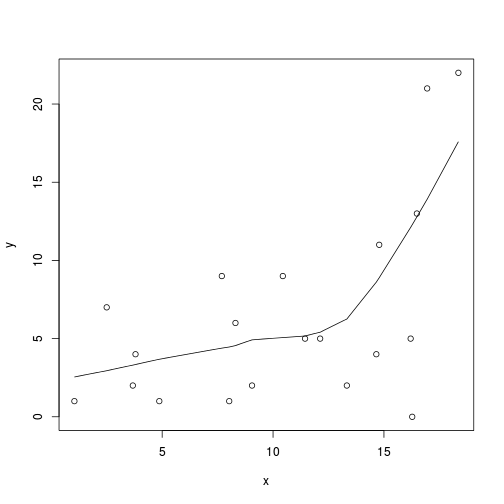
plot(y~x, data.nb, log="y")
with(data.nb, lines(lowess(y~x)))
rug(jitter(data.nb$y), side=2)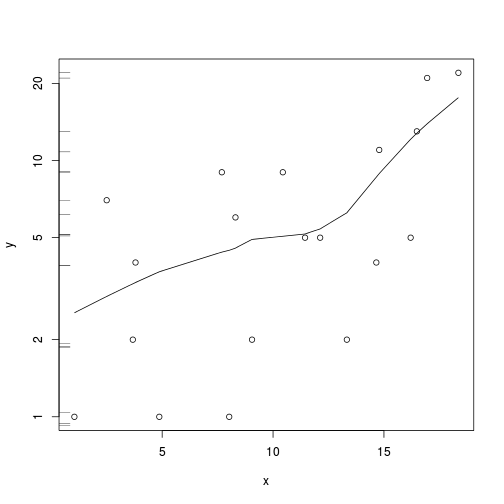
hist(data.nb$y, br=10)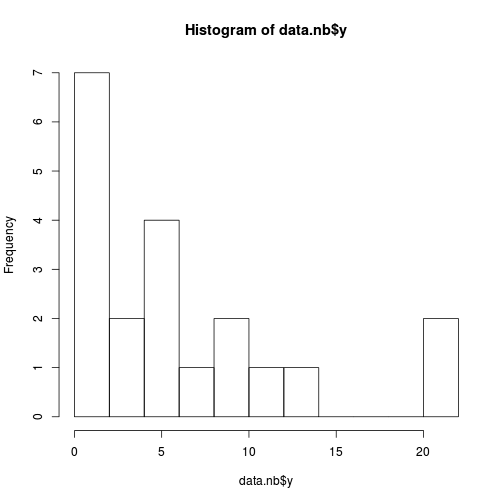
boxplot(data.nb$y, horizontal=TRUE)
rug(jitter(data.nb$y), side=1)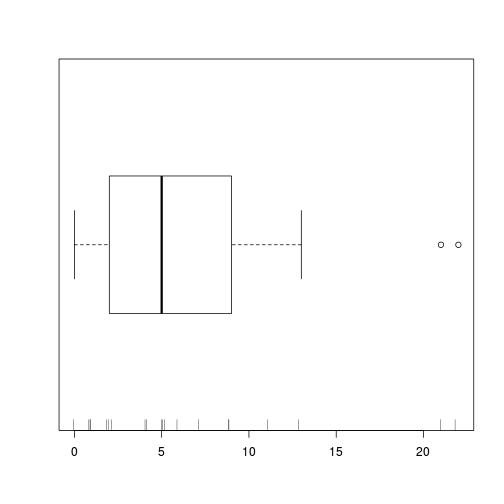
#Zero inflation
#proportion of 0's in the data
data.nb.tab<-table(data.nb$y==0)
data.nb.tab/sum(data.nb.tab)
FALSE TRUE
0.95 0.05 #proportion of 0's expected from a Poisson distribution
mu <- mean(data.nb$y)
cnts <- rpois(1000, mu)
hist(cnts)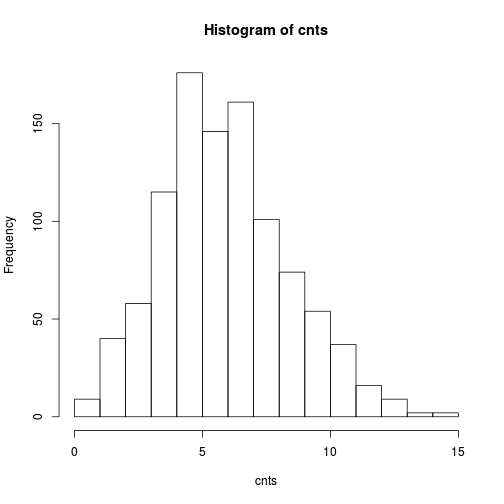
tab <- table(cnts == 0)
tab/sum(tab)
FALSE TRUE
0.999 0.001 #fit model
library(MASS)
data.nb.glm <- glm.nb(y~x, data=data.nb)
#Model validation
par(mfrow=c(2,3))
plot(data.nb.glm, ask=F,which=1:6)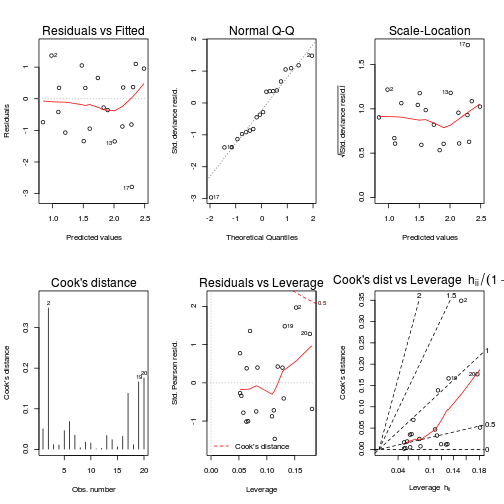
data.ss <- sum(resid(data.nb1, type = "pearson")^2)Error: object 'data.nb1' not founddata.ss/data.nb1$df.residError: object 'data.ss' not founddata.nb1 <- glm(y~x, data=data.nb, family='poisson')
plot(data.nb1, ask=F,which=1:6)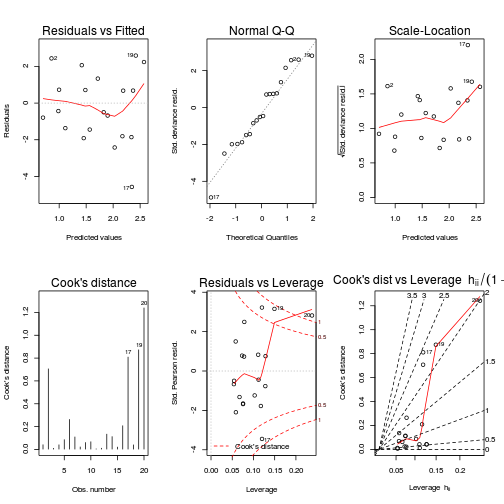
1-pchisq(data.nb1$deviance, data.nb1$df.resid)[1] 8.6e-08#goodness of fit
data.nb.resid <- sum(resid(data.nb.glm, type = "pearson")^2)
1 - pchisq(data.nb.resid, data.nb.glm$df.resid)[1] 0.5825#Deviance based
1-pchisq(data.nb.glm$deviance, data.nb.glm$df.resid)[1] 0.2407data.nb.glmG <- glm(y~x, data=data.nb, family="gaussian")
AIC(data.nb.glm, data.nb.glmG) df AIC
data.nb.glm 3 115.8
data.nb.glmG 3 128.2#Poisson deviance
data.nb.glm$deviance[1] 21.81#Gaussian deviance
data.nb.glmG$deviance[1] 527.6summary(data.nb.glm)
Call:
glm.nb(formula = y ~ x, data = data.nb, init.theta = 2.359878187,
link = log)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.787 -0.894 -0.317 0.442 1.366
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.7454 0.4253 1.75 0.0797
x 0.0949 0.0344 2.76 0.0058
(Intercept) .
x **
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for Negative Binomial(2.36) family taken to be 1)
Null deviance: 30.443 on 19 degrees of freedom
Residual deviance: 21.806 on 18 degrees of freedom
AIC: 115.8
Number of Fisher Scoring iterations: 1
Theta: 2.36
Std. Err.: 1.10
2 x log-likelihood: -109.85 library(gmodels)
ci(data.nb.glm) Estimate CI lower CI upper Std. Error
(Intercept) 0.74543 -0.14818 1.6390 0.42534
x 0.09494 0.02265 0.1672 0.03441
p-value
(Intercept) 0.079682
x 0.0057921-(data.nb.glm$deviance/data.nb.glm$null)[1] 0.2837par(mfrow=c(1,1),mar = c(4, 5, 0, 0))
plot(y ~ x, data = data.nb, type = "n", ann = F, axes = F)
points(y ~ x, data = data.nb, pch = 16)
xs <- seq(0, 20, l = 1000)
ys <- predict(data.nb.glm, newdata = data.frame(x = xs), type = "link", se = T)
ys$lwr <- exp(ys$fit - 2*ys$se.fit)
ys$upr <- exp(ys$fit + 2*ys$se.fit)
ys$fit <- exp(ys$fit)
lines(ys$fit ~ xs, col = "black")
lines(ys$lwr ~ xs, col = "black", lty = 2)
lines(ys$upr ~ xs, col = "black", lty = 2)
axis(1)
mtext("X", 1, cex = 1.5, line = 3)
axis(2, las = 2)
mtext("Abundance of Y", 2, cex = 1.5, line = 3)
box(bty = "l")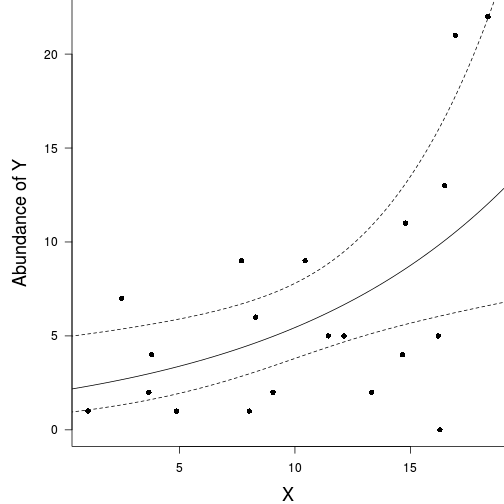
data.zip <- read.csv('../data/data.zip.csv', strip.white=T)
head(data.zip) y x
1 0 1.042
2 3 2.498
3 1 3.677
4 4 3.798
5 5 4.871
6 1 7.690ggplot(data.zip, aes(y=y, x=x))+geom_point()Error: could not find function "ggplot"plot(y~x, data.zip)
with(data.zip, lines(lowess(y~x)))
plot(y~x, data.zip, log="y")
with(data.zip, lines(lowess(y~x)))
rug(jitter(data.pois$y), side=2)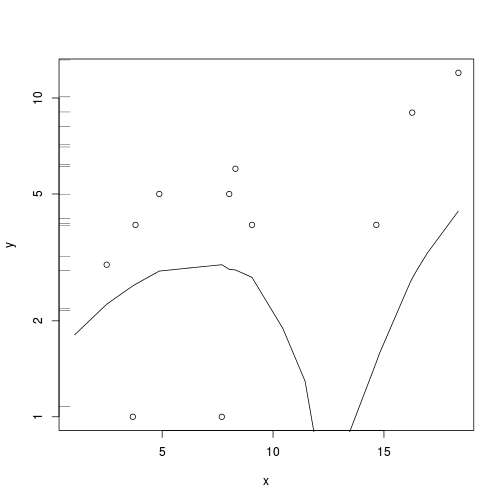
hist(data.zip$y, br=20)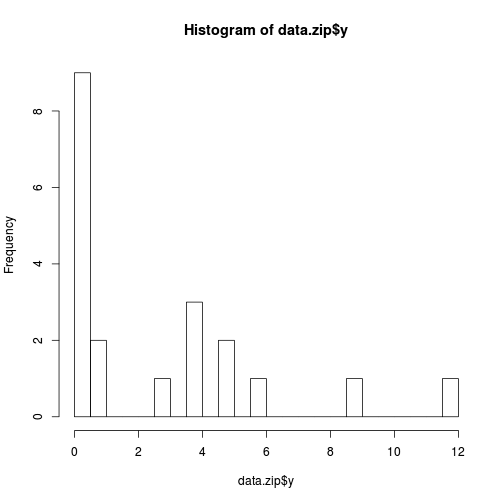
boxplot(data.zip$y, horizontal=TRUE)
rug(jitter(data.zip$y), side=1)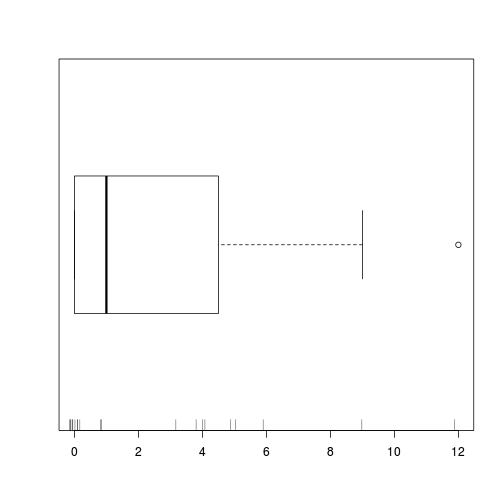
#Zero inflation
#proportion of 0's in the data
data.zip.tab<-table(data.zip$y==0)
data.zip.tab/sum(data.zip.tab)
FALSE TRUE
0.55 0.45 #proportion of 0's expected from a Poisson distribution
mu <- mean(data.zip$y)
cnts <- rpois(1000, mu)
data.zip.tab <- table(cnts == 0)
data.zip.tab/sum(data.zip.tab)
FALSE TRUE
0.929 0.071 summary(glm(y~x, data.zip, family="poisson"))
Call:
glm(formula = y ~ x, family = "poisson", data = data.zip)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.541 -2.377 -0.975 1.174 3.638
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.6705 0.3302 2.03 0.042
x 0.0296 0.0266 1.11 0.266
(Intercept) *
x
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 85.469 on 19 degrees of freedom
Residual deviance: 84.209 on 18 degrees of freedom
AIC: 124
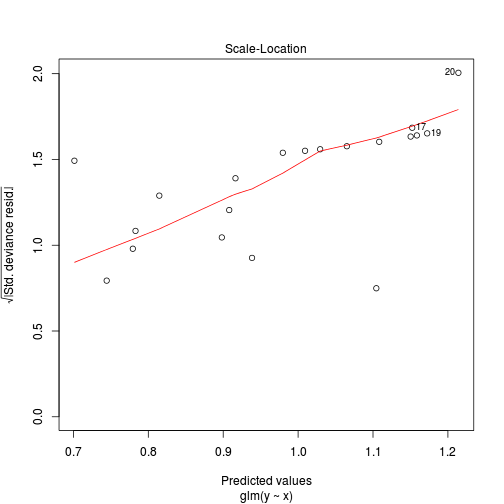
Number of Fisher Scoring iterations: 6plot(glm(y~x, data.zip, family="poisson"))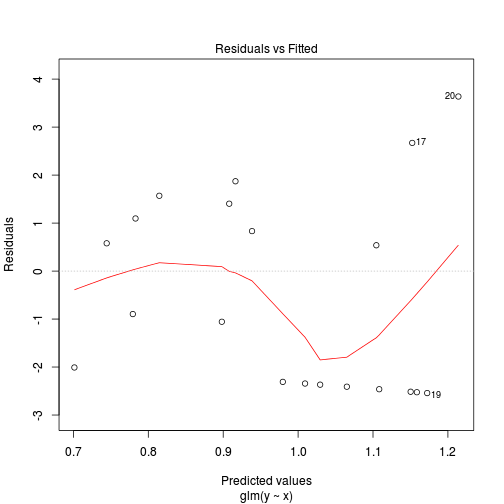

library(pscl)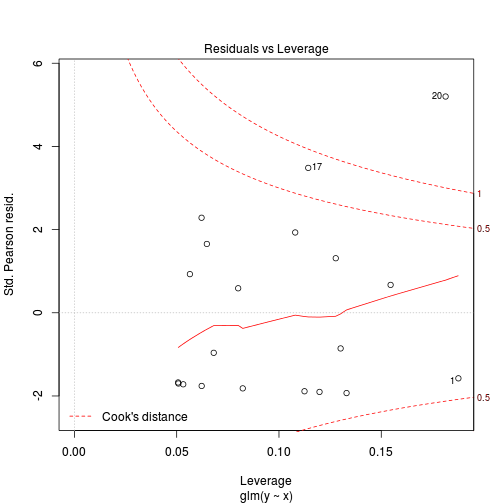
data.zip.zip <- zeroinfl(y ~ x | 1, dist = "poisson", data = data.zip)
plot(resid(data.zip.zip)~fitted(data.zip.zip))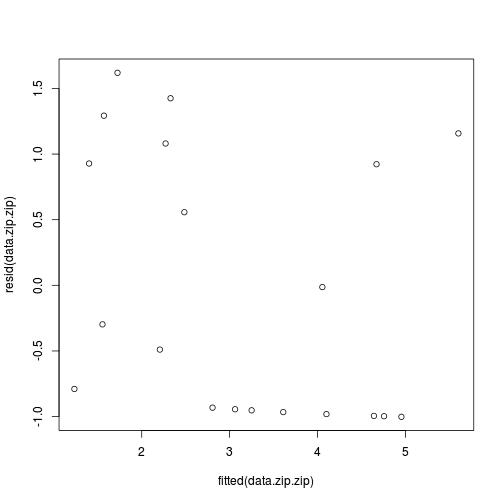
summary(data.zip.zip)
Call:
zeroinfl(formula = y ~ x | 1, data = data.zip,
dist = "poisson")
Pearson residuals:
Min 1Q Median 3Q Max
-1.001 -0.956 -0.393 0.966 1.619
Count model coefficients (poisson with log link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.7047 0.3196 2.21 0.02745
x 0.0873 0.0253 3.45 0.00056
(Intercept) *
x ***
Zero-inflation model coefficients (binomial with logit link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.229 0.456 -0.5 0.62
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Number of iterations in BFGS optimization: 13
Log-likelihood: -36.2 on 3 Dfdata.zip.zip1 <- zeroinfl(y ~ x | x, dist = "poisson", data = data.zip)
plot(resid(data.zip.zip1)~fitted(data.zip.zip1))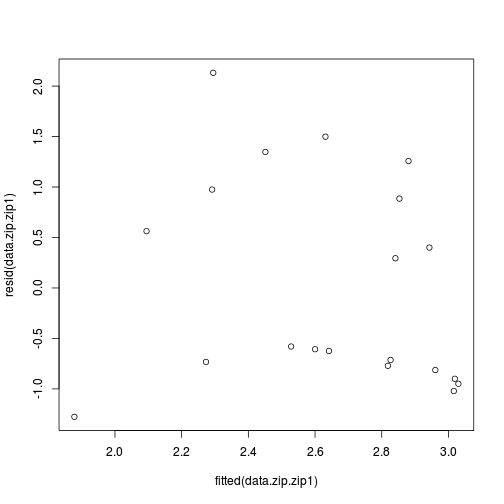
summary(data.zip.zip1)
Call:
zeroinfl(formula = y ~ x | x, data = data.zip,
dist = "poisson")
Pearson residuals:
Min 1Q Median 3Q Max
-1.276 -0.781 -0.593 0.908 2.132
Count model coefficients (poisson with log link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.6111 0.3300 1.85 0.06404
x 0.0939 0.0257 3.65 0.00027
(Intercept) .
x ***
Zero-inflation model coefficients (binomial with logit link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.731 1.890 -1.44 0.15
x 0.217 0.146 1.49 0.14
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Number of iterations in BFGS optimization: 17
Log-likelihood: -34.4 on 4 DfAIC(data.zip.zip, data.zip.zip1) df AIC
data.zip.zip 3 78.34
data.zip.zip1 4 76.81par(mar = c(4, 5, 0, 0))
plot(y ~ x, data = data.zip, type = "n", ann = F, axes = F)
points(y ~ x, data = data.zip, pch = 16)
xs <- seq(0, 20, l = 1000)
#ys <- predict(data.pois.glm, newdata = data.frame(x = xs), type = "response", se = T)
coefs <- coef(data.zip.zip)[1:2]
mm <- model.matrix(~x, data=data.frame(x=xs))
fit <- coefs %*% t(mm)
se <- sqrt(diag(mm %*% vcov(data.zip.zip)[-3,-3] %*% t(mm)))
lwr <- as.vector(exp(fit - 2*se))
upr <- as.vector(exp(fit + 2*se))
fit <- as.vector(exp(fit))
lines(fit ~ xs, col = "black")
lines(lwr ~ xs, col = "black", lty = 2)
lines(upr ~ xs, col = "black", lty = 2)
polygon(c(xs,rev(xs)), c(lwr,rev(upr)), border=NA, col="#0000FF50")
#lines(ys$fit - 2 * ys$se.fit ~ xs, col = "black", type = "l", lty = 2)
#lines(ys$fit + 2 * ys$se.fit ~ xs, col = "black", type = "l", lty = 2)
axis(1)
mtext("X", 1, cex = 1.5, line = 3)
axis(2, las = 2)
mtext("Abundance of Y", 2, cex = 1.5, line = 3)
box(bty = "l")