Linear models
\[ \begin{align*} y_{i} &= \beta_0 + \beta_1 \times x_{i} + \varepsilon_i\\ \epsilon_i&\sim\mathcal{N}(0, \sigma^2) \\ \end{align*} \]

\[ \begin{align*} y_{i} &= \beta_0 + \beta_1 \times x_{i} + \varepsilon_i\\ \epsilon_i&\sim\mathcal{N}(0, \sigma^2) \\ \end{align*} \]

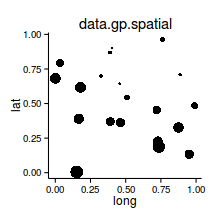
\(y \sim{} N(\mu, \sigma^2)\\ \mu = \beta_0 + \beta_1 x_1 + \beta_2 x_2\)
Polynomial \(y \sim{} N(\mu, \sigma^2)\\ \mu = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_2 x^3\)
data.gp.lm <- lm(y~x+I(x^2), data=data.gp)
#OR
data.gp.lm <- lm(y~poly(x,2), data=data.gp)
summary(data.gp.lm)
Call:
lm(formula = y ~ poly(x, 2), data = data.gp)
Residuals:
1 2 3 4 5
-0.00866 0.12987 -0.58009 0.57143 -0.11255
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.58e-17 2.63e-01 0.00 1.00
poly(x, 2)1 1.05e+00 5.88e-01 1.78 0.22
poly(x, 2)2 -2.87e+00 5.88e-01 -4.87 0.04
(Intercept)
poly(x, 2)1
poly(x, 2)2 *
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.588 on 2 degrees of freedom
Multiple R-squared: 0.931, Adjusted R-squared: 0.861
F-statistic: 13.4 on 2 and 2 DF, p-value: 0.0693newdata <- data.frame(x=seq(min(data.gp$x),
max(data.gp$x), l=100))
pred <- predict(data.gp.lm, newdata=newdata,
interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) x fit lwr upr
1 -8.000 -1.991 -4.220 0.2376
2 -7.879 -1.859 -4.011 0.2922
3 -7.758 -1.730 -3.808 0.3483
4 -7.636 -1.603 -3.612 0.4061
5 -7.515 -1.478 -3.422 0.4655
6 -7.394 -1.356 -3.240 0.5268ggplot(newdata, aes(y=fit, x=x))+
geom_point(data=data.gp, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()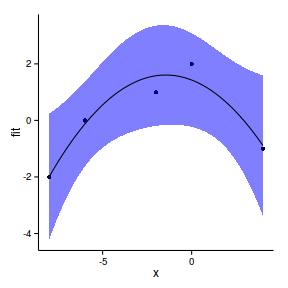
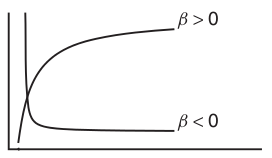
Power (\(y = \alpha x^\beta\))
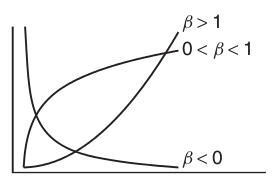
Exponential (\(y = \alpha e^{\beta x}\))
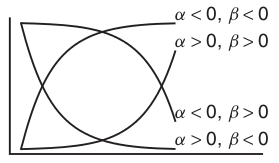
Asymptotic exponential
\(y = \alpha + (\beta - \alpha) e^{-e^{\gamma} x}\) 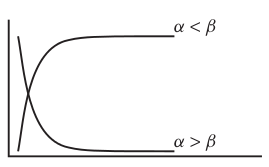
Michaelis-Menton (\(y = \frac{\alpha x}{\beta + x}\))
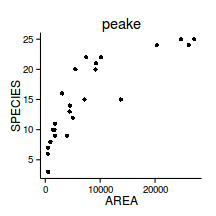
nls(y ~ a * exp(b*x), start=list(a=1, b=1), data=data)peake <- read.table('../data/peake.csv', header=T, sep=',', strip.white=T)
head(peake) AREA SPECIES INDIV
1 516.0 3 18
2 469.1 7 60
3 462.2 6 57
4 938.6 8 100
5 1357.2 10 48
6 1773.7 9 118library(car)
scatterplot(SPECIES~AREA,data=peake)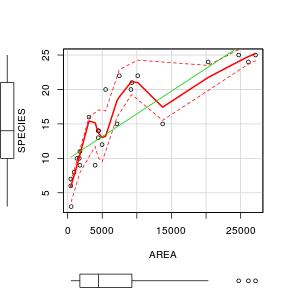
#Linear
peake.lmLin<-lm(SPECIES~AREA, data=peake)
#Polynomial
peake.lm <- lm(SPECIES~AREA+poly(AREA,2), data=peake)
#Power function
peake.nls <- nls(SPECIES~alpha*AREA^beta, data=peake,
start=list(alpha=0.1,beta=0.5))
#Assymptotic exponential
peake.nls.as <- nls(SPECIES~SSasymp(AREA,a,b,c),
data=peake)#Linear
plot(resid(peake.lmLin)~fitted(peake.lmLin))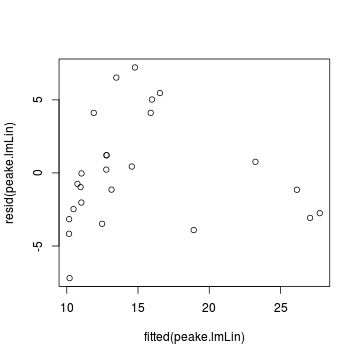
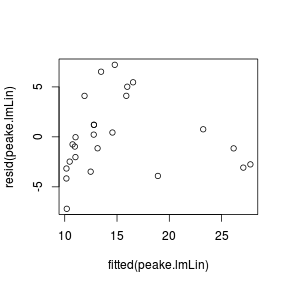

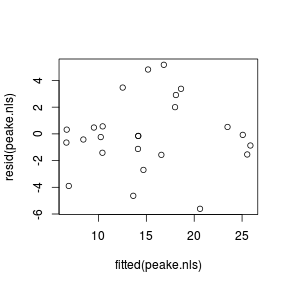
Error: object 'peake.nls1' not found#calculate AIC for the linear model
AIC(peake.lmLin, peake.lm, peake.nls, peake.nls.as) df AIC
peake.lmLin 3 141.1
peake.lm 4 129.5
peake.nls 3 125.1
peake.nls.as 4 125.8#assess the goodness of fit between pairs of models
peake.nls1 <- peake.nls.as
anova(peake.lmLin,peake.lm)Analysis of Variance Table
Model 1: SPECIES ~ AREA
Model 2: SPECIES ~ AREA + poly(AREA, 2)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 23 325
2 22 189 1 136 15.8 0.00064 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(peake.nls, peake.nls1)Analysis of Variance Table
Model 1: SPECIES ~ alpha * AREA^beta
Model 2: SPECIES ~ SSasymp(AREA, a, b, c)
Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)
1 23 172
2 22 163 1 9.14 1.24 0.28## calculate mean-square residual of the models
deviance(peake.lmLin)/df.residual(peake.lmLin)[1] 14.13deviance(peake.lm)/df.residual(peake.lm)[1] 8.602deviance(peake.nls)/df.residual(peake.nls)[1] 7.469deviance(peake.nls1)/df.residual(peake.nls1)[1] 7.393xs<-with(peake,seq(min(AREA),max(AREA),l=100))
ys <- predict(peake.nls.as, data.frame(AREA=xs))
se <- sqrt(apply(attr(ys,"gradient"),1,function(x)
sum(vcov(peake.nls.as)*outer(x,x))))
newdata <- data.frame(AREA=xs, fit=ys,
lower=ys-2*se,
upper=ys+2*se)
head(newdata) AREA fit lower upper
1 462.2 6.248 3.907 8.589
2 731.8 6.962 4.866 9.057
3 1001.3 7.647 5.760 9.534
4 1270.8 8.305 6.590 10.021
5 1540.3 8.938 7.357 10.519
6 1809.8 9.546 8.065 11.026ggplot(newdata, aes(y=fit, x=AREA))+
geom_point(data=peake, aes(y=SPECIES))+
geom_ribbon(aes(ymin=lower,ymax=upper),
fill='blue',alpha=0.5)+
geom_line()+
theme_classic()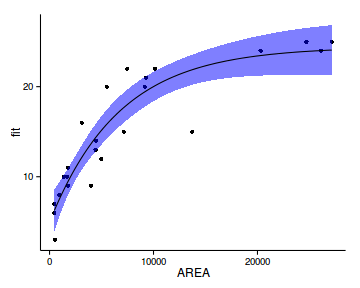
grad <- deriv3(~alpha*AREA^beta, c("alpha","beta"),
function(alpha,beta,AREA) NULL)
peake.nls<-nls(SPECIES~grad(alpha,beta,AREA),
data=peake,start=list(alpha=0.1,beta=1))
xs<-with(peake,seq(min(AREA),max(AREA),l=100))
ys <- predict(peake.nls, data.frame(AREA=xs))
se.fit <- sqrt(apply(attr(ys,"gradient"),1,function(x)
sum(vcov(peake.nls)*outer(x,x))))
newdata1 <- data.frame(AREA=xs, fit=ys, lower=ys-se.fit,
upper=ys+se.fit)
head(newdata1) AREA fit lower upper
1 462.2 6.648 5.908 7.388
2 731.8 7.749 7.004 8.494
3 1001.3 8.604 7.864 9.343
4 1270.8 9.316 8.586 10.046
5 1540.3 9.933 9.215 10.652
6 1809.8 10.482 9.776 11.189ggplot(newdata1, aes(y=fit, x=AREA))+
geom_point(data=peake, aes(y=SPECIES))+
geom_ribbon(aes(ymin=lower,ymax=upper),
fill='blue',alpha=0.5)+
geom_line()+
theme_classic()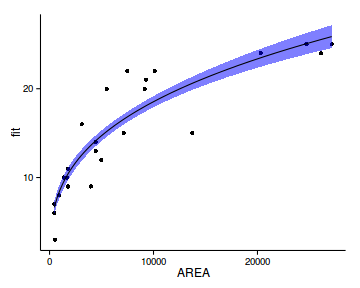
ggplot(newdata, aes(y=fit, x=AREA))+
geom_point(data=peake, aes(y=SPECIES))+
geom_ribbon(aes(ymin=lower,ymax=upper),
fill='blue',alpha=0.5)+
geom_line(color='blue')+
geom_ribbon(data=newdata1,aes(ymin=lower,ymax=upper),
fill='red',alpha=0.5)+
geom_line(data=newdata1,aes(y=fit,x=AREA), color='red')+
theme_classic()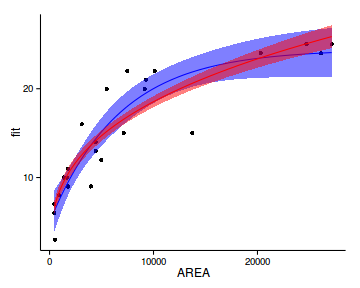
newdata2 <- rbind(cbind(Model='Power',newdata1),
cbind(Model='Assymp',newdata))
ggplot(data=newdata2, aes(y=fit, x=AREA))+
geom_point(data=peake, aes(y=SPECIES))+
geom_ribbon(aes(ymin=lower,ymax=upper, fill=Model),alpha=0.5)+
geom_line(aes(fill=Model, color=Model))+
theme_classic()
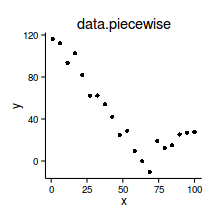
data.piecewise <- read.csv('../data/data.piecewise.csv')
ggplot(data.piecewise, aes(y=y, x=x))+geom_point()+
theme_classic()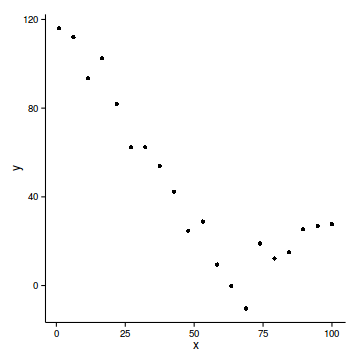
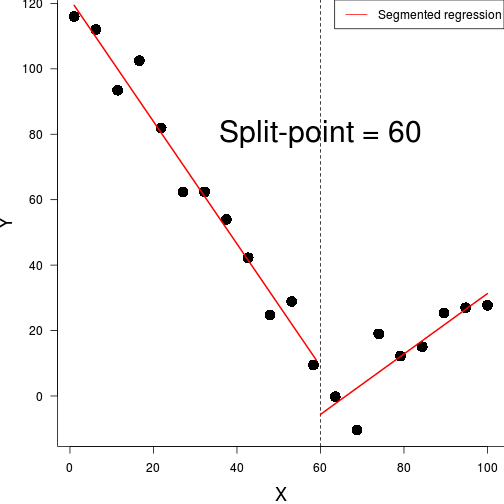
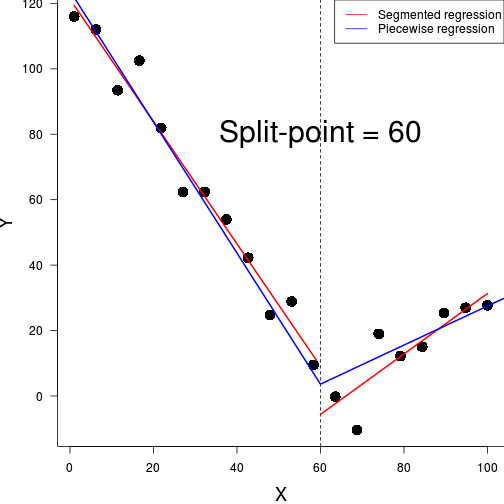
#for a breakpoint of 60
data.piecewise.lm <- lm(y~x+I(ifelse(x>60,x-60,0)),
data=data.piecewise)
summary(data.piecewise.lm)
Call:
lm(formula = y ~ x + I(ifelse(x > 60, x - 60, 0)), data = data.piecewise)
Residuals:
Min 1Q Median 3Q Max
-19.18 -3.79 1.28 3.96 11.99
Coefficients:
Estimate Std. Error
(Intercept) 123.824 4.057
x -2.003 0.104
I(ifelse(x > 60, x - 60, 0)) 2.600 0.239
t value Pr(>|t|)
(Intercept) 30.5 2.7e-16 ***
x -19.3 5.5e-13 ***
I(ifelse(x > 60, x - 60, 0)) 10.9 4.4e-09 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.61 on 17 degrees of freedom
Multiple R-squared: 0.965, Adjusted R-squared: 0.961
F-statistic: 233 on 2 and 17 DF, p-value: 4.45e-13#for a breakpoint of 60
before <- function(x) ifelse(x<60, 60-x,0)
after <- function(x) ifelse(x<60, 0, x-60)
seq(0,100,by=10) [1] 0 10 20 30 40 50 60 70 80 90 100before(seq(0,100,by=10)) [1] 60 50 40 30 20 10 0 0 0 0 0after(seq(0,100,by=10)) [1] 0 0 0 0 0 0 0 10 20 30 40before(70)[1] 0data.piecewise.lm <- lm(y~before(x)+after(x), data=data.piecewise)
summary(data.piecewise.lm)
Call:
lm(formula = y ~ before(x) + after(x), data = data.piecewise)
Residuals:
Min 1Q Median 3Q Max
-19.18 -3.79 1.28 3.96 11.99
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.619 3.413 1.06 0.3038
before(x) 2.003 0.104 19.27 5.5e-13
after(x) 0.597 0.162 3.68 0.0018
(Intercept)
before(x) ***
after(x) **
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.61 on 17 degrees of freedom
Multiple R-squared: 0.965, Adjusted R-squared: 0.961
F-statistic: 233 on 2 and 17 DF, p-value: 4.45e-13#What if we dont know the breakpoint?
before <- function(x,bp) ifelse(x<bp, bp-x,0)
after <- function(x,bp) ifelse(x<bp, 0, x-bp)
piecewise <- function(bp) {
mod <- lm(y ~ before(x,bp)+after(x,bp),
data=data.piecewise)
sum(resid(mod)^2)
}
search.range <- c(min(data.piecewise$x,na.rm=TRUE)+0.5,
max(data.piecewise$x, na.rm=TRUE)-0.5)
search.range <- c(0,100)
pw.opt <- optimize(piecewise, interval = search.range)
(bp <- pw.opt$minimum)[1] 65.51bp[1] 65.51mod <- lm(y ~ before(x,bp)+after(x,bp),
data=data.piecewise)
summary(mod)
Call:
lm(formula = y ~ before(x, bp) + after(x, bp), data = data.piecewise)
Residuals:
Min 1Q Median 3Q Max
-11.549 -3.860 0.466 2.362 12.651
Coefficients:
Estimate Std. Error t value
(Intercept) -1.9740 2.9397 -0.67
before(x, bp) 1.8868 0.0809 23.31
after(x, bp) 0.9829 0.1657 5.93
Pr(>|t|)
(Intercept) 0.51
before(x, bp) 2.4e-14 ***
after(x, bp) 1.6e-05 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.55 on 17 degrees of freedom
Multiple R-squared: 0.974, Adjusted R-squared: 0.971
F-statistic: 317 on 2 and 17 DF, p-value: 3.48e-14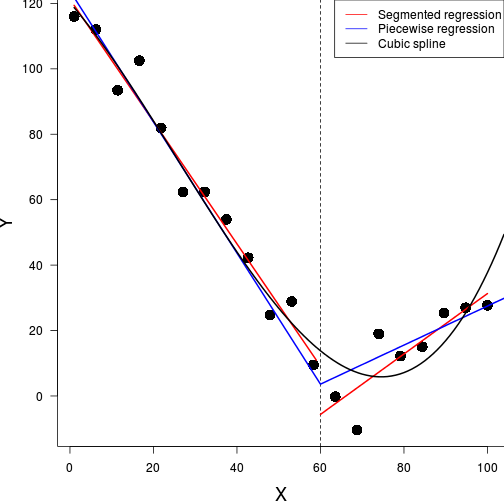
library(splines)data.gp <- read.csv('../data/data.gp.csv')
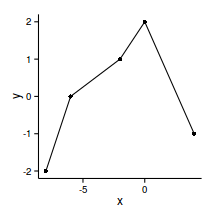
head(data.gp) x y
1 -8 -2
2 -6 0
3 -2 1
4 0 2
5 4 -1ggplot(data.gp, aes(y=y, x=x))+geom_point()+geom_line()+
theme_classic()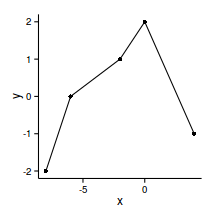
library(splines)
data.gp.lm <- lm(y~x, data=data.gp)
summary(data.gp.lm)
Call:
lm(formula = y ~ x, data = data.gp)
Residuals:
1 2 3 4 5
-1.386 0.395 0.956 1.737 -1.702
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.263 0.884 0.30 0.79
x 0.110 0.180 0.61 0.59
Residual standard error: 1.72 on 3 degrees of freedom
Multiple R-squared: 0.11, Adjusted R-squared: -0.187
F-statistic: 0.369 on 1 and 3 DF, p-value: 0.586newdata <- data.frame(x=seq(min(data.gp$x),
max(data.gp$x), l=100))
pred <- predict(data.gp.lm, newdata=newdata,interval='confidence')
newdata <- cbind(newdata,pred)
ggplot(newdata, aes(y=fit, x=x))+
geom_point(data=data.gp, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()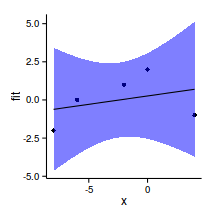
library(splines)
ns(data.gp$x) 1
[1,] 0.0000
[2,] 0.1336
[3,] 0.4009
[4,] 0.5345
[5,] 0.8018
attr(,"degree")
[1] 3
attr(,"knots")
numeric(0)
attr(,"Boundary.knots")
[1] -8 4
attr(,"intercept")
[1] FALSE
attr(,"class")
[1] "ns" "basis" "matrix"ns(data.gp$x,k=3) 1 2
[1,] 0.0000 0.0000
[2,] 0.1701 -0.1523
[3,] 0.4472 -0.2869
[4,] 0.5228 -0.1842
[5,] 0.4730 0.5634
attr(,"degree")
[1] 3
attr(,"knots")
[1] 3
attr(,"Boundary.knots")
[1] -8 4
attr(,"intercept")
[1] FALSE
attr(,"class")
[1] "ns" "basis" "matrix"ns(data.gp$x, df=4) 1 2 3 4
[1,] 0.00000 0.0000 0.0000 0.00000
[2,] 0.08333 -0.1836 0.4590 -0.27541
[3,] 0.65000 0.2124 0.1357 -0.08145
[4,] 0.26667 0.5860 0.2018 -0.05439
[5,] 0.00000 -0.1579 0.3947 0.76316
attr(,"degree")
[1] 3
attr(,"knots")
25% 50% 75%
-6 -2 0
attr(,"Boundary.knots")
[1] -8 4
attr(,"intercept")
[1] FALSE
attr(,"class")
[1] "ns" "basis" "matrix"data.gp.lm <- lm(y~ns(x,df=2), data=data.gp)
summary(data.gp.lm)
Call:
lm(formula = y ~ ns(x, df = 2), data = data.gp)
Residuals:
1 2 3 4 5
-0.099 0.264 -0.657 0.622 -0.130
Coefficients:
Estimate Std. Error t value
(Intercept) -1.901 0.586 -3.24
ns(x, df = 2)1 5.815 1.427 4.07
ns(x, df = 2)2 -1.258 0.855 -1.47
Pr(>|t|)
(Intercept) 0.083 .
ns(x, df = 2)1 0.055 .
ns(x, df = 2)2 0.279
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.676 on 2 degrees of freedom
Multiple R-squared: 0.909, Adjusted R-squared: 0.817
F-statistic: 9.93 on 2 and 2 DF, p-value: 0.0915data.gp.ns <- lm(y~ns(x), data=data.gp)
summary(data.gp.ns)
Call:
lm(formula = y ~ ns(x), data = data.gp)
Residuals:
1 2 3 4 5
-1.386 0.395 0.956 1.737 -1.702
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.614 1.270 -0.48 0.66
ns(x) 1.641 2.700 0.61 0.59
Residual standard error: 1.72 on 3 degrees of freedom
Multiple R-squared: 0.11, Adjusted R-squared: -0.187
F-statistic: 0.369 on 1 and 3 DF, p-value: 0.586newdata <- data.frame(
x=seq(min(data.gp$x),
max(data.gp$x), l=100))
pred <- predict(data.gp.lm, newdata=newdata,
interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) x fit lwr upr
1 -8.000 -1.901 -4.423 0.6213
2 -7.879 -1.798 -4.248 0.6515
3 -7.758 -1.696 -4.075 0.6836
4 -7.636 -1.593 -3.905 0.7177
5 -7.515 -1.491 -3.737 0.7540
6 -7.394 -1.390 -3.572 0.7925newdata.ns <- newdata
pred.ns <- predict(data.gp.ns, newdata=newdata,
interval='confidence')
newdata.ns <- cbind(newdata.ns,pred.ns)
head(newdata) x fit lwr upr
1 -8.000 -1.901 -4.423 0.6213
2 -7.879 -1.798 -4.248 0.6515
3 -7.758 -1.696 -4.075 0.6836
4 -7.636 -1.593 -3.905 0.7177
5 -7.515 -1.491 -3.737 0.7540
6 -7.394 -1.390 -3.572 0.7925ggplot(newdata, aes(y=fit, x=x))+
geom_point(data=data.gp, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()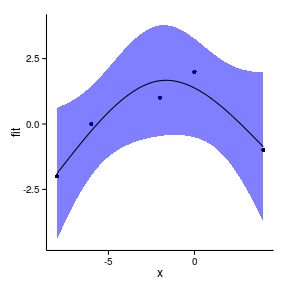
ggplot(newdata.ns, aes(y=fit, x=x))+
geom_point(data=data.gp, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()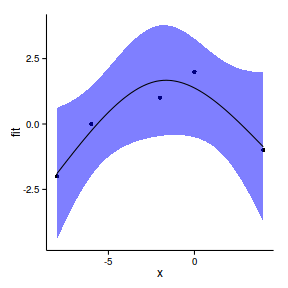
data.gp.ns1 <- lm(y~ns(x,k=1), data=data.gp)
summary(data.gp.ns1)
Call:
lm(formula = y ~ ns(x, k = 1), data = data.gp)
Residuals:
1 2 3 4 5
-0.1720 0.3791 -0.5652 0.4162 -0.0581
Coefficients:
Estimate Std. Error t value
(Intercept) -1.828 0.492 -3.72
ns(x, k = 1)1 5.587 1.245 4.49
ns(x, k = 1)2 -2.183 0.778 -2.81
Pr(>|t|)
(Intercept) 0.065 .
ns(x, k = 1)1 0.046 *
ns(x, k = 1)2 0.107
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.579 on 2 degrees of freedom
Multiple R-squared: 0.933, Adjusted R-squared: 0.866
F-statistic: 13.9 on 2 and 2 DF, p-value: 0.0669newdata1 <- data.frame(
x=seq(min(data.gp$x),
max(data.gp$x), l=100))
pred1 <- predict(data.gp.ns1, newdata=newdata1,
interval='confidence')
newdata1 <- cbind(newdata1,pred1)
head(newdata1) x fit lwr upr
1 -8.000 -1.828 -3.944 0.2883
2 -7.879 -1.738 -3.800 0.3241
3 -7.758 -1.648 -3.656 0.3611
4 -7.636 -1.558 -3.515 0.3994
5 -7.515 -1.468 -3.374 0.4390
6 -7.394 -1.378 -3.236 0.4801ggplot(newdata1, aes(y=fit, x=x))+
geom_point(data=data.gp, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()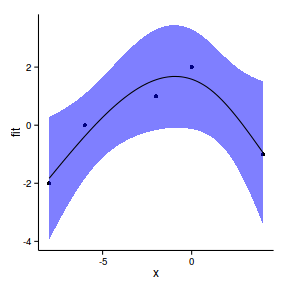
anova(data.gp.lm,data.gp.ns, data.gp.ns1)Analysis of Variance Table
Model 1: y ~ ns(x, df = 2)
Model 2: y ~ ns(x)
Model 3: y ~ ns(x, k = 1)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 2 0.91
2 3 8.90 -1 -7.99 17.5 0.053 .
3 2 0.67 1 8.23 18.0 0.051 .
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1AIC(data.gp.lm, data.gp.ns, data.gp.ns1) df AIC
data.gp.lm 4 13.70
data.gp.ns 3 23.07
data.gp.ns1 4 12.14library(splines)
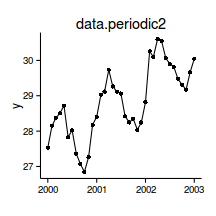
data.periodic2 <- read.csv('../data/data.periodic2.csv')
head(data.periodic2) y time month day
1 27.53 2000-01-01 1 0.002807
2 28.15 2000-02-01 2 0.089825
3 28.37 2000-03-01 3 0.171228
4 28.51 2000-04-01 4 0.258246
5 28.72 2000-05-01 5 0.342456
6 27.83 2000-06-01 6 0.429474library(lubridate)
data.periodic2$Dt.num <- decimal_date(as.Date(data.periodic2$time))
data.periodic2.ns <- lm(y~ns(Dt.num), data=data.periodic2)
summary(data.periodic2.ns)
Call:
lm(formula = y ~ ns(Dt.num), data = data.periodic2)
Residuals:
Min 1Q Median 3Q Max
-1.3889 -0.5069 -0.0134 0.5559 1.1787
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 27.645 0.227 121.67 < 2e-16
ns(Dt.num) 2.959 0.488 6.06 6.4e-07
(Intercept) ***
ns(Dt.num) ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.706 on 35 degrees of freedom
Multiple R-squared: 0.512, Adjusted R-squared: 0.498
F-statistic: 36.8 on 1 and 35 DF, p-value: 6.35e-07newdata <- data.frame(
Dt.num=seq(min(data.periodic2$Dt.num),
max(data.periodic2$Dt.num), l=100))
pred <- predict(data.periodic2.ns, newdata=newdata,
interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) Dt.num fit lwr upr
1 2000 27.64 27.18 28.11
2 2000 27.67 27.21 28.12
3 2000 27.69 27.24 28.14
4 2000 27.72 27.28 28.16
5 2000 27.74 27.31 28.17
6 2000 27.76 27.34 28.19ggplot(newdata, aes(y=fit, x=Dt.num))+
geom_point(data=data.periodic2, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()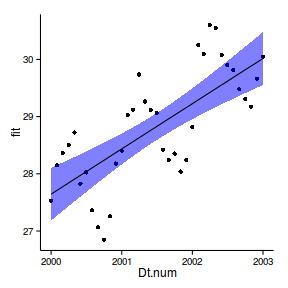
data.periodic2.ns <- lm(y~ns(Dt.num,df=4), data=data.periodic2)
summary(data.periodic2.ns)
Call:
lm(formula = y ~ ns(Dt.num, df = 4), data = data.periodic2)
Residuals:
Min 1Q Median 3Q Max
-1.224 -0.556 0.103 0.488 1.289
Coefficients:
Estimate Std. Error t value
(Intercept) 28.097 0.424 66.27
ns(Dt.num, df = 4)1 0.699 0.567 1.23
ns(Dt.num, df = 4)2 1.889 0.554 3.41
ns(Dt.num, df = 4)3 1.340 1.095 1.22
ns(Dt.num, df = 4)4 1.799 0.512 3.51
Pr(>|t|)
(Intercept) <2e-16 ***
ns(Dt.num, df = 4)1 0.2265
ns(Dt.num, df = 4)2 0.0018 **
ns(Dt.num, df = 4)3 0.2303
ns(Dt.num, df = 4)4 0.0013 **
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.702 on 32 degrees of freedom
Multiple R-squared: 0.558, Adjusted R-squared: 0.503
F-statistic: 10.1 on 4 and 32 DF, p-value: 2.07e-05newdata <- data.frame(Dt.num=seq(min(data.periodic2$Dt.num), max(data.periodic2$Dt.num), l=100))
pred <- predict(data.periodic2.ns, newdata=newdata, interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) Dt.num fit lwr upr
1 2000 28.10 27.23 28.96
2 2000 28.08 27.27 28.89
3 2000 28.07 27.31 28.82
4 2000 28.05 27.35 28.76
5 2000 28.04 27.38 28.69
6 2000 28.02 27.41 28.64ggplot(newdata, aes(y=fit, x=Dt.num))+
geom_point(data=data.periodic2, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()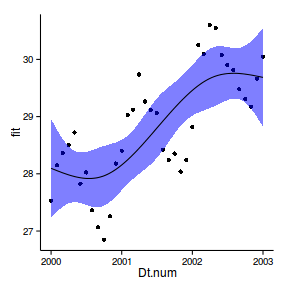
data.periodic2.ns <- lm(y~ns(Dt.num,df=7), data=data.periodic2)
summary(data.periodic2.ns)
Call:
lm(formula = y ~ ns(Dt.num, df = 7), data = data.periodic2)
Residuals:
Min 1Q Median 3Q Max
-0.5270 -0.2335 0.0417 0.2266 0.5712
Coefficients:
Estimate Std. Error t value
(Intercept) 27.893 0.241 115.62
ns(Dt.num, df = 7)1 -1.980 0.344 -5.76
ns(Dt.num, df = 7)2 3.720 0.422 8.81
ns(Dt.num, df = 7)3 -1.815 0.385 -4.72
ns(Dt.num, df = 7)4 3.513 0.400 8.78
ns(Dt.num, df = 7)5 1.105 0.333 3.32
ns(Dt.num, df = 7)6 2.401 0.623 3.86
ns(Dt.num, df = 7)7 1.359 0.281 4.83
Pr(>|t|)
(Intercept) < 2e-16 ***
ns(Dt.num, df = 7)1 3.1e-06 ***
ns(Dt.num, df = 7)2 1.1e-09 ***
ns(Dt.num, df = 7)3 5.5e-05 ***
ns(Dt.num, df = 7)4 1.2e-09 ***
ns(Dt.num, df = 7)5 0.00242 **
ns(Dt.num, df = 7)6 0.00059 ***
ns(Dt.num, df = 7)7 4.0e-05 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.325 on 29 degrees of freedom
Multiple R-squared: 0.915, Adjusted R-squared: 0.894
F-statistic: 44.3 on 7 and 29 DF, p-value: 8.44e-14newdata <- data.frame(Dt.num=seq(min(data.periodic2$Dt.num), max(data.periodic2$Dt.num), l=100))
pred <- predict(data.periodic2.ns, newdata=newdata, interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) Dt.num fit lwr upr
1 2000 27.89 27.40 28.39
2 2000 27.95 27.51 28.39
3 2000 28.01 27.62 28.40
4 2000 28.07 27.72 28.42
5 2000 28.12 27.81 28.43
6 2000 28.17 27.88 28.45ggplot(newdata, aes(y=fit, x=Dt.num))+
geom_point(data=data.periodic2, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()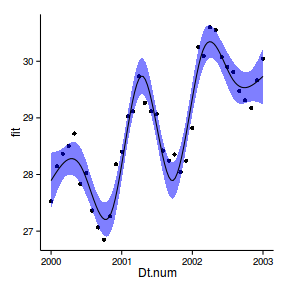
data.periodic2.ns <- lm(y~ns(Dt.num,df=2) + ns(month,df=3), data=data.periodic2)
summary(data.periodic2.ns)
Call:
lm(formula = y ~ ns(Dt.num, df = 2) + ns(month, df = 3), data = data.periodic2)
Residuals:
Min 1Q Median 3Q Max
-0.4370 -0.2057 0.0185 0.1677 0.6720
Coefficients:
Estimate Std. Error t value
(Intercept) 27.363 0.150 182.14
ns(Dt.num, df = 2)1 3.268 0.276 11.82
ns(Dt.num, df = 2)2 2.354 0.151 15.63
ns(month, df = 3)1 -1.453 0.188 -7.73
ns(month, df = 3)2 0.772 0.298 2.59
ns(month, df = 3)3 -1.679 0.139 -12.07
Pr(>|t|)
(Intercept) < 2e-16 ***
ns(Dt.num, df = 2)1 5.1e-13 ***
ns(Dt.num, df = 2)2 3.0e-16 ***
ns(month, df = 3)1 1.0e-08 ***
ns(month, df = 3)2 0.014 *
ns(month, df = 3)3 3.0e-13 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.266 on 31 degrees of freedom
Multiple R-squared: 0.939, Adjusted R-squared: 0.929
F-statistic: 95.1 on 5 and 31 DF, p-value: <2e-16newdata <- data.frame(
Dt.num=seq(min(data.periodic2$Dt.num), max(data.periodic2$Dt.num), l=100),
month=6)
pred <- predict(data.periodic2.ns, newdata=newdata, interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) Dt.num month fit lwr upr
1 2000 6 27.87 27.60 28.15
2 2000 6 27.90 27.63 28.17
3 2000 6 27.93 27.67 28.19
4 2000 6 27.95 27.70 28.21
5 2000 6 27.98 27.73 28.22
6 2000 6 28.00 27.77 28.24ggplot(newdata, aes(y=fit, x=Dt.num))+
geom_point(data=data.periodic2, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()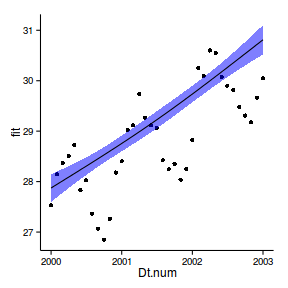
newdata <- data.frame(
month=seq(1,12, l=100),
Dt.num=2001.5)
pred <- predict(data.periodic2.ns, newdata=newdata, interval='confidence')
newdata <- cbind(newdata,pred)
head(newdata) month Dt.num fit lwr upr
1 1.000 2002 28.72 28.44 29.00
2 1.111 2002 28.78 28.51 29.05
3 1.222 2002 28.84 28.58 29.10
4 1.333 2002 28.90 28.65 29.15
5 1.444 2002 28.96 28.72 29.20
6 1.556 2002 29.02 28.79 29.25ggplot(newdata, aes(y=fit, x=month))+
geom_point(data=data.periodic2, aes(y=y))+
geom_ribbon(aes(ymin=lwr,ymax=upr),fill='blue',alpha=0.5)+
geom_line()+
theme_classic()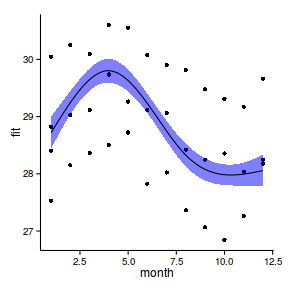
\(y \sim{} N(\mu, \sigma^2)\\ \mu = \beta_0 + \beta_1 x_1 + \beta_2 x_2\)
\(y \sim{} Pois(\mu, \sigma^2)\\ g(\mu) = \beta_0 + \beta_1 x_1 + \beta_2 x_2\)
\(y \sim{} Pois(\mu, \sigma^2)\\ g(\mu) = \beta_0 + \beta_1 x_1 + \beta_2 x_2\)
\(y \sim{} Pois(\mu, \sigma^2)\\ g(\mu) = \beta_0 + f(x_1) + f(x_2)\)
library(mgcv)
dat.gam <- gam(y~s(x1)+s(x2)+s(x3), data=dat)
summary(dat.gam)
Family: gaussian
Link function: identity
Formula:
y ~ s(x1) + s(x2) + s(x3)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.728 0.103 75.3 <2e-16
(Intercept) ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x1) 2.82 3.51 77.82 <2e-16 ***
s(x2) 8.21 8.83 84.16 <2e-16 ***
s(x3) 1.00 1.00 0.01 0.92
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.725 Deviance explained = 73.3%
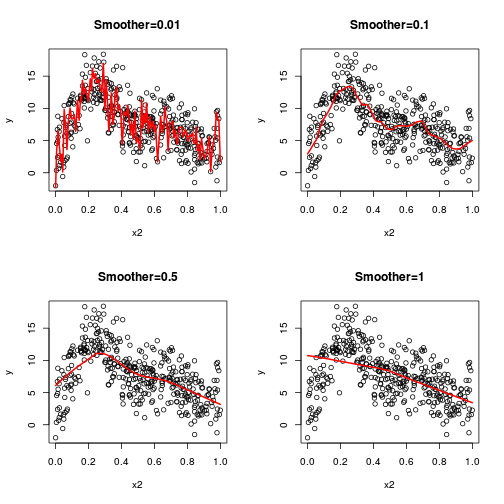
GCV = 4.3588 Scale est. = 4.2168 n = 400plot(dat.gam, pages=1)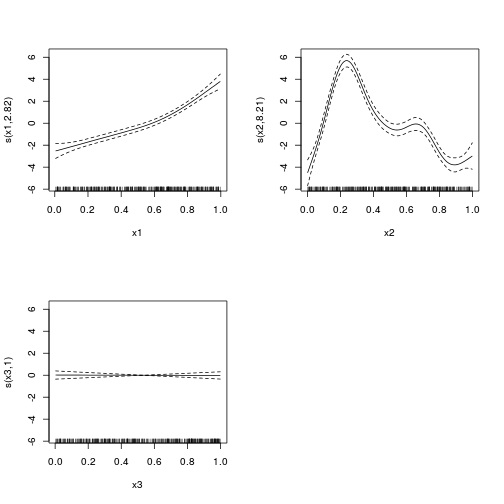
plot(dat.gam, select=2, shade=TRUE)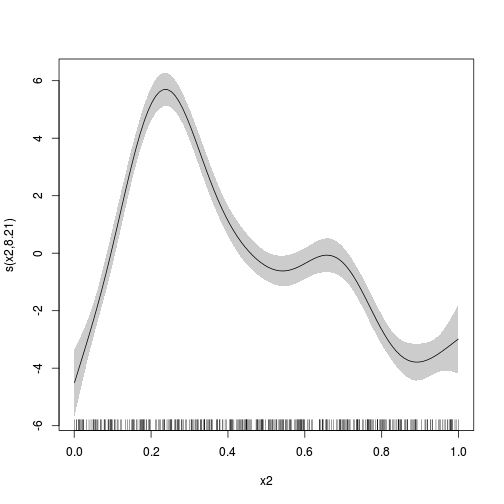
library(mgcv)
dat.gam <- gam(y~s(x2,x3), data=dat)
summary(dat.gam)
Family: gaussian
Link function: identity
Formula:
y ~ s(x2, x3)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.728 0.135 57.4 <2e-16
(Intercept) ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x2,x3) 25.9 28.4 15.9 <2e-16 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.528 Deviance explained = 55.8%
GCV = 7.7651 Scale est. = 7.2425 n = 400plot(dat.gam, pages=1, scheme=2)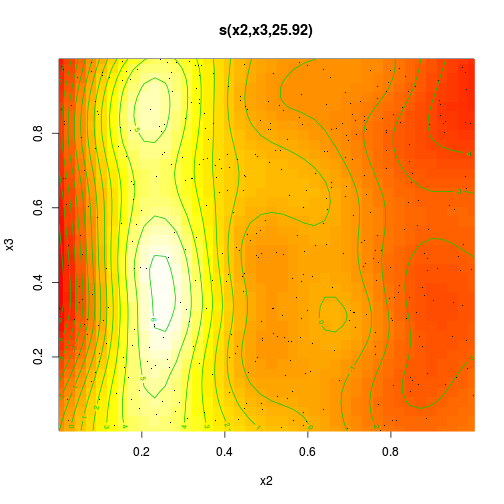
vis.gam(dat.gam, theta=35)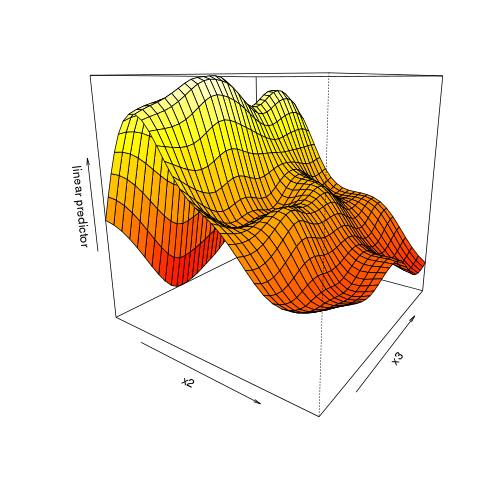
vis.gam(dat.gam, theta=35, se=2)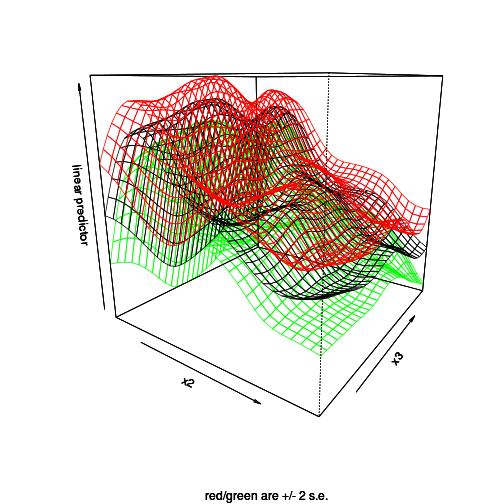
data.gp <- read.csv('../data/data.gp.csv')
ggplot(data.gp, aes(y=y, x=x))+geom_point()+geom_line()+
theme_classic()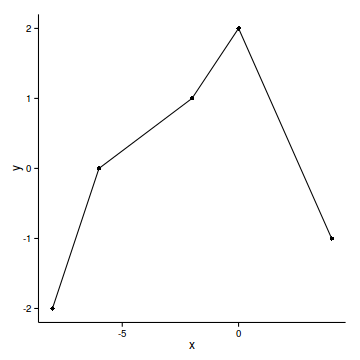
library(mgcv)
data.gp.gam <- gam(y~s(x,k=3), data=data.gp)
summary(data.gp.gam)
Family: gaussian
Link function: identity
Formula:
y ~ s(x, k = 3)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.93e-17 2.87e-01 0 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x) 1.95 2 10.9 0.081 .
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.835 Deviance explained = 91.5%
GCV = 1.0045 Scale est. = 0.41203 n = 5plot(data.gp.gam, resid=TRUE, cex=4)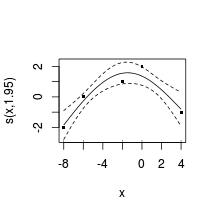
xs <- seq(-8,4,l=100)
pred <- predict(data.gp.gam,
newdata = data.frame(x=xs), se=TRUE)
dat <- data.frame(x=xs,fit=pred$fit,
lower=pred$fit-2*pred$se.fit,
upper=pred$fit+2*pred$se.fit)
ggplot(data=dat, aes(y=fit, x=x)) +
geom_ribbon(data=dat,
aes(y=fit, x=x, ymin=lower, ymax=upper),
fill='blue',alpha=0.2)+
geom_line()+
geom_point(data=data.gp, aes(y=y,x=x))+
theme_classic()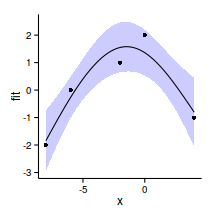
AIC(data.gp.gam)[1] 15.2library(mgcv)
data.gp.gam <- gam(y~s(x,k=3), data=data.gp)
summary(data.gp.gam)
Family: gaussian
Link function: identity
Formula:
y ~ s(x, k = 3)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.93e-17 2.87e-01 0 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x) 1.95 2 10.9 0.081 .
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.835 Deviance explained = 91.5%
GCV = 1.0045 Scale est. = 0.41203 n = 5xs <- seq(-8,4,l=100)
pred <- predict(data.gp.gam,
newdata = data.frame(x=xs), se=TRUE)
dat <- data.frame(x=xs,fit=pred$fit,
lower=pred$fit-2*pred$se.fit,
upper=pred$fit+2*pred$se.fit)
head(dat) x fit lower upper
1 -8.000 -1.841 -2.946 -0.7368
2 -7.879 -1.742 -2.815 -0.6687
3 -7.758 -1.643 -2.686 -0.5998
4 -7.636 -1.544 -2.557 -0.5302
5 -7.515 -1.445 -2.430 -0.4597
6 -7.394 -1.346 -2.304 -0.3885ggplot(data=dat, aes(y=fit, x=x)) +
geom_ribbon(data=dat,
aes(y=fit, x=x, ymin=lower, ymax=upper),
fill='blue',alpha=0.2)+
geom_line()+
geom_point(data=data.gp, aes(y=y,x=x))+
theme_classic()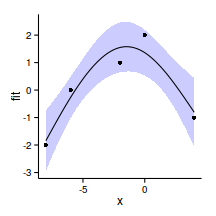
AIC(data.gp.gam)[1] 15.2