Factorial ANOVA

| Factor | MS | F-ratio (both fixed) | F-ratio (A fixed, B random) | F-ratio (both random) |
|---|---|---|---|---|
| A | \(MS_A\) | \(MS_A/MS_{Resid}\) | \(MS_A/MS_{A:B}\) | \(MS_A/MS_{A:B}\) |
| B | \(MS_B\) | \(MS_B/MS_{Resid}\) | \(MS_B/MS_{Resid}\) | \(MS_B/MS_{A:B}\) |
| A:B | \(MS_{A:B}\) | \(MS_{A:B}/MS_{Resid}\) | \(MS_{A:B}/MS_{Resid}\) | \(MS_{A:B}/MS_{A:B}\) |
\[SS_{TOTAL} = SS_{A} + SS_{B} + SS_{A:B} + SS_{Resid}\]
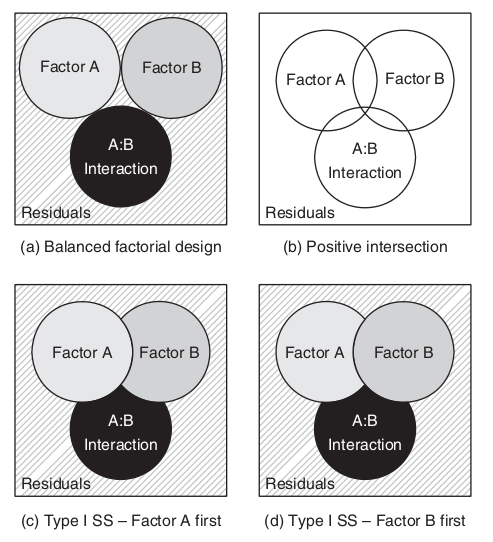
\[SS_{TOTAL} = SS_{A} + SS_{B} + SS_{A:B} + SS_{Resid}\]
\[SS_{TOTAL} \ne SS_{A} + SS_{B} + SS_{A:B} + SS_{Resid}\]

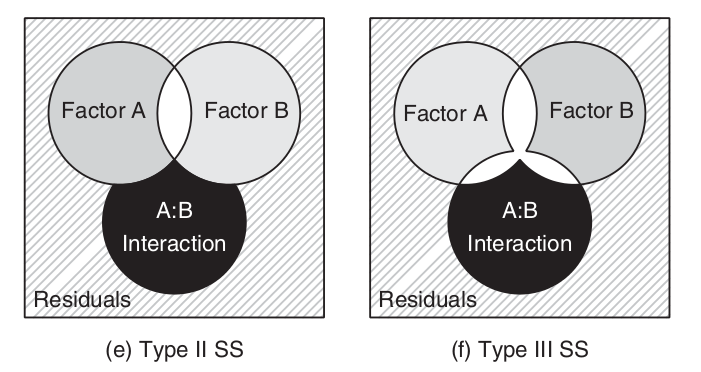
\[SS_{TOTAL} = SS_{A} + SS_{B} + SS_{A:B} + SS_{Resid}\]
\[SS_{TOTAL} \ne SS_{A} + SS_{B} + SS_{A:B} + SS_{Resid}\]
starling <- read.csv('../data/starling.csv',strip.white=T)
head(starling) SITUATION MONTH MASS GROUP
1 S1 November 78 S1Nov
2 S1 November 88 S1Nov
3 S1 November 87 S1Nov
4 S1 November 88 S1Nov
5 S1 November 83 S1Nov
6 S1 November 82 S1Novboxplot(MASS~SITUATION*MONTH, data=starling)
#Check for balance
replications(MASS~SITUATION*MONTH, data=starling) SITUATION MONTH SITUATION:MONTH
20 40 10 !is.list(replications(MASS~SITUATION*MONTH, data=starling))[1] TRUEstarling.lm <- lm(MASS~SITUATION*MONTH, data=starling)
# setup a 2x6 plotting device with small margins
par(mfrow = c(2, 1))
plot(starling.lm,ask=F,which=1:2)
plot(rstandard(starling.lm)~starling$SITUATION)
plot(rstandard(starling.lm)~starling$MONTH)
#Examine interaction plot - to help understand coefficients
library(car)
with(starling,interaction.plot(SITUATION, MONTH, MASS))
summary(starling.lm)
Call:
lm(formula = MASS ~ SITUATION * MONTH, data = starling)
Residuals:
Min 1Q Median 3Q Max
-7.4 -3.2 -0.4 2.9 9.2
Coefficients:
Estimate Std. Error
(Intercept) 90.80 1.33
SITUATIONS2 -0.60 1.88
SITUATIONS3 -2.60 1.88
SITUATIONS4 -6.60 1.88
MONTHNovember -7.20 1.88
SITUATIONS2:MONTHNovember -3.60 2.66
SITUATIONS3:MONTHNovember -2.40 2.66
SITUATIONS4:MONTHNovember -1.60 2.66
t value Pr(>|t|)
(Intercept) 68.26 < 2e-16 ***
SITUATIONS2 -0.32 0.75069
SITUATIONS3 -1.38 0.17121
SITUATIONS4 -3.51 0.00078 ***
MONTHNovember -3.83 0.00027 ***
SITUATIONS2:MONTHNovember -1.35 0.18023
SITUATIONS3:MONTHNovember -0.90 0.37000
SITUATIONS4:MONTHNovember -0.60 0.54946
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.21 on 72 degrees of freedom
Multiple R-squared: 0.64, Adjusted R-squared: 0.605
F-statistic: 18.3 on 7 and 72 DF, p-value: 9.55e-14anova(starling.lm)Analysis of Variance Table
Response: MASS
Df Sum Sq Mean Sq F value Pr(>F)
SITUATION 3 574 191 10.82 6.0e-06
MONTH 1 1656 1656 93.60 1.2e-14
SITUATION:MONTH 3 34 11 0.64 0.59
Residuals 72 1274 18
SITUATION ***
MONTH ***
SITUATION:MONTH
Residuals
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1library(multcomp)
summary(glht(starling.lm, linfct=mcp(SITUATION="Tukey")))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = MASS ~ SITUATION * MONTH, data = starling)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
S2 - S1 == 0 -0.60 1.88 -0.32 0.9887
S3 - S1 == 0 -2.60 1.88 -1.38 0.5146
S4 - S1 == 0 -6.60 1.88 -3.51 0.0043
S3 - S2 == 0 -2.00 1.88 -1.06 0.7129
S4 - S2 == 0 -6.00 1.88 -3.19 0.0111
S4 - S3 == 0 -4.00 1.88 -2.13 0.1547
S2 - S1 == 0
S3 - S1 == 0
S4 - S1 == 0 **
S3 - S2 == 0
S4 - S2 == 0 *
S4 - S3 == 0
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)#Added model
summary(glht(lm(MASS~SITUATION+MONTH, data=starling), linfct=mcp(SITUATION="Tukey")))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = MASS ~ SITUATION + MONTH, data = starling)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
S2 - S1 == 0 -2.40 1.32 -1.82 0.2733
S3 - S1 == 0 -3.80 1.32 -2.88 0.0263
S4 - S1 == 0 -7.40 1.32 -5.60 <0.001
S3 - S2 == 0 -1.40 1.32 -1.06 0.7147
S4 - S2 == 0 -5.00 1.32 -3.79 0.0017
S4 - S3 == 0 -3.60 1.32 -2.73 0.0394
S2 - S1 == 0
S3 - S1 == 0 *
S4 - S1 == 0 ***
S3 - S2 == 0
S4 - S2 == 0 **
S4 - S3 == 0 *
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)confint(glht(lm(MASS~SITUATION+MONTH, data=starling), linfct=mcp(SITUATION="Tukey")))
Simultaneous Confidence Intervals
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = MASS ~ SITUATION + MONTH, data = starling)
Quantile = 2.628
95% family-wise confidence level
Linear Hypotheses:
Estimate lwr upr
S2 - S1 == 0 -2.400 -5.870 1.070
S3 - S1 == 0 -3.800 -7.270 -0.330
S4 - S1 == 0 -7.400 -10.870 -3.930
S3 - S2 == 0 -1.400 -4.870 2.070
S4 - S2 == 0 -5.000 -8.470 -1.530
S4 - S3 == 0 -3.600 -7.070 -0.130#Population means
library(effects)
plot(allEffects(starling.lm))
starling.eff <- allEffects(starling.lm)
(starling.means <- with(starling.eff[[1]],data.frame(Fit=fit, Lower=lower, Upper=upper, x))) Fit Lower Upper SITUATION MONTH
1 90.8 88.15 93.45 S1 January
2 90.2 87.55 92.85 S2 January
3 88.2 85.55 90.85 S3 January
4 84.2 81.55 86.85 S4 January
5 83.6 80.95 86.25 S1 November
6 79.4 76.75 82.05 S2 November
7 78.6 75.95 81.25 S3 November
8 75.4 72.75 78.05 S4 Novemberstarling.means <- starling.means[order(starling.means$SITUATION),]
opar<-par(mar=c(5,5,1,1))
xs <- barplot(starling.means$Fit,ylim=range(c(starling.means[,2:3])), beside=T, axes=F, ann=F, axisnames=F, xpd=F, axis.lty=2, col=c(0,1), space=c(1,0,1,0,1,0))
arrows(xs,starling.means$Fit, xs, starling.means$Upper, code=2, length=0.05, ang=90)
axis(2, las=1)
axis(1, at=apply(matrix(xs,nrow=2),2,median), lab=c("Situation 1", "Situation 2", "Situation 3", "Situation 4"))
mtext(2,text="Mass (g) of starlings", line=3, cex=1.25)
legend("topright",leg=c("January","November"), fill=c(0,1), col=c(0,1), bty="n", cex=1)
box(bty="l")
par(opar)
#Raw data
opar<-par(mar=c(5,5,1,1))
star.means <- with(starling,tapply(MASS, list(MONTH,SITUATION),mean))
star.sds <- with(starling,tapply(MASS, list(MONTH,SITUATION),sd))
star.len <- with(starling,tapply(MASS, list(MONTH,SITUATION),length))
star.ses <-star.sds/sqrt(star.len)
xs <- barplot(star.means,ylim=range(starling$MASS), beside=T, axes=F, ann=F, axisnames=F, xpd=F, axis.lty=2, col=c(0,1))
arrows(xs,star.means, xs, star.means+star.ses, code=2, length=0.05, ang=90)
axis(2, las=1)
axis(1, at=apply(xs,2,median), lab=c("Situation 1", "Situation 2", "Situation 3", "Situation 4"))
mtext(2,text="Mass (g) of starlings", line=3, cex=1.25)
legend("topright",leg=c("January","November"), fill=c(0,1), col=c(0,1), bty="n", cex=1)
box(bty="l")
par(opar)
#Effect of month separately for each situtation
xmat <- expand.grid(SITUATION=levels(starling$SITUATION), MONTH=levels(starling$MONTH))
mm <- model.matrix(~SITUATION*MONTH, xmat)
mm.jan <- mm[xmat$MONTH=="January",]
mm.nov <- mm[xmat$MONTH=="November",]
mm.sit <- mm.jan-mm.nov
data.frame(confint(glht(starling.lm, mm.sit))$confint,Situation=xmat[xmat$MONTH=="January",1]) Estimate lwr upr Situation
1 7.2 2.399 12.0 S1
2 10.8 5.999 15.6 S2
3 9.6 4.799 14.4 S3
4 8.8 3.999 13.6 S4starling.lm2 <- lm(MASS~SITUATION+MONTH, data=starling)
summary(starling.lm2)
Call:
lm(formula = MASS ~ SITUATION + MONTH, data = starling)
Residuals:
Min 1Q Median 3Q Max
-7.35 -2.80 -0.25 3.10 8.75
Coefficients:
Estimate Std. Error t value
(Intercept) 91.750 1.044 87.87
SITUATIONS2 -2.400 1.321 -1.82
SITUATIONS3 -3.800 1.321 -2.88
SITUATIONS4 -7.400 1.321 -5.60
MONTHNovember -9.100 0.934 -9.74
Pr(>|t|)
(Intercept) < 2e-16 ***
SITUATIONS2 0.0732 .
SITUATIONS3 0.0052 **
SITUATIONS4 3.3e-07 ***
MONTHNovember 5.8e-15 ***
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.18 on 75 degrees of freedom
Multiple R-squared: 0.63, Adjusted R-squared: 0.611
F-statistic: 32 on 4 and 75 DF, p-value: 1.53e-15summary(glht(starling.lm2, linfct=mcp(SITUATION="Tukey")))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = MASS ~ SITUATION + MONTH, data = starling)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
S2 - S1 == 0 -2.40 1.32 -1.82 0.2734
S3 - S1 == 0 -3.80 1.32 -2.88 0.0263
S4 - S1 == 0 -7.40 1.32 -5.60 <0.001
S3 - S2 == 0 -1.40 1.32 -1.06 0.7147
S4 - S2 == 0 -5.00 1.32 -3.79 0.0018
S4 - S3 == 0 -3.60 1.32 -2.73 0.0391
S2 - S1 == 0
S3 - S1 == 0 *
S4 - S1 == 0 ***
S3 - S2 == 0
S4 - S2 == 0 **
S4 - S3 == 0 *
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)#Worked examples
stehman <- read.table('../data/stehman.csv', header=T, sep=',', strip.white=T)
head(stehman) PH HEALTH GROUP BRATING
1 3 D D3 0.0
2 3 D D3 0.8
3 3 D D3 0.8
4 3 D D3 0.8
5 3 D D3 0.8
6 3 D D3 0.8stehman$PH <- as.factor(stehman$PH)
boxplot(BRATING~HEALTH*PH, data=stehman)
replications(BRATING~HEALTH*PH, data=stehman)$HEALTH
HEALTH
D H
67 28
$PH
PH
3 5.5 7
34 30 31
$`HEALTH:PH`
PH
HEALTH 3 5.5 7
D 23 23 21
H 11 7 10!is.list(replications(BRATING~HEALTH*PH, data=stehman))[1] FALSE#contrasts(stehman$HEALTH)<-contr.sum
#contrasts(stehman$PH)<-contr.sum
stehman.lm <- lm(BRATING~HEALTH*PH, data=stehman)
par(mfrow=c(2,2))
plot(stehman.lm, which=1:2,ask=FALSE)
plot(rstandard(stehman.lm)~stehman$HEALTH)
plot(rstandard(stehman.lm)~stehman$PH)
summary(stehman.lm)
Call:
lm(formula = BRATING ~ HEALTH * PH, data = stehman)
Residuals:
Min 1Q Median 3Q Max
-1.2286 -0.3238 -0.0087 0.3818 0.9913
Coefficients:
Estimate Std. Error t value
(Intercept) 1.1913 0.1056 11.28
HEALTHH 0.4269 0.1857 2.30
PH5.5 -0.3826 0.1494 -2.56
PH7 -0.0675 0.1529 -0.44
HEALTHH:PH5.5 -0.0070 0.2868 -0.02
HEALTHH:PH7 -0.2107 0.2690 -0.78
Pr(>|t|)
(Intercept) <2e-16 ***
HEALTHH 0.024 *
PH5.5 0.012 *
PH7 0.660
HEALTHH:PH5.5 0.981
HEALTHH:PH7 0.435
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.506 on 89 degrees of freedom
Multiple R-squared: 0.196, Adjusted R-squared: 0.15
F-statistic: 4.33 on 5 and 89 DF, p-value: 0.00143library(car)
Anova(stehman.lm, type="III")Anova Table (Type III tests)
Response: BRATING
Sum Sq Df F value Pr(>F)
(Intercept) 32.6 1 127.25 <2e-16 ***
HEALTH 1.4 1 5.29 0.024 *
PH 1.9 2 3.71 0.028 *
HEALTH:PH 0.2 2 0.37 0.690
Residuals 22.8 89
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1library(car)
with(stehman,interaction.plot(PH,HEALTH,BRATING))
library(multcomp)
summary(glht(stehman.lm, linfct=mcp(PH="Tukey")))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = BRATING ~ HEALTH * PH, data = stehman)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
5.5 - 3 == 0 -0.3826 0.1493 -2.56 0.032
7 - 3 == 0 -0.0675 0.1529 -0.44 0.898
7 - 5.5 == 0 0.3151 0.1529 2.06 0.104
5.5 - 3 == 0 *
7 - 3 == 0
7 - 5.5 == 0
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)confint(glht(stehman.lm, linfct=mcp(PH="Tukey")))
Simultaneous Confidence Intervals
Multiple Comparisons of Means: Tukey Contrasts
Fit: lm(formula = BRATING ~ HEALTH * PH, data = stehman)
Quantile = 2.384
95% family-wise confidence level
Linear Hypotheses:
Estimate lwr upr
5.5 - 3 == 0 -0.3826 -0.7386 -0.0266
7 - 3 == 0 -0.0675 -0.4319 0.2969
7 - 5.5 == 0 0.3151 -0.0493 0.6795#fit polynomials
stehman.lm2<-lm(BRATING~PH*HEALTH, data=stehman, contrasts=list(PH=contr.poly(3,scores=c(3,5.5,7)), HEALTH=contr.treatment))
summary(stehman.lm2)
Call:
lm(formula = BRATING ~ PH * HEALTH, data = stehman, contrasts = list(PH = contr.poly(3,
scores = c(3, 5.5, 7)), HEALTH = contr.treatment))
Residuals:
Min 1Q Median 3Q Max
-1.2286 -0.3238 -0.0087 0.3818 0.9913
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.0413 0.0619 16.81 <2e-16
PH.L -0.0879 0.1077 -0.82 0.4162
PH.Q 0.2751 0.1069 2.57 0.0117
HEALTH2 0.3543 0.1155 3.07 0.0029
PH.L:HEALTH2 -0.1360 0.1899 -0.72 0.4758
PH.Q:HEALTH2 -0.1008 0.2099 -0.48 0.6323
(Intercept) ***
PH.L
PH.Q *
HEALTH2 **
PH.L:HEALTH2
PH.Q:HEALTH2
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.506 on 89 degrees of freedom
Multiple R-squared: 0.196, Adjusted R-squared: 0.15
F-statistic: 4.33 on 5 and 89 DF, p-value: 0.00143confint(stehman.lm2) 2.5 % 97.5 %
(Intercept) 0.91821 1.1643
PH.L -0.30184 0.1260
PH.Q 0.06273 0.4875
HEALTH2 0.12475 0.5839
PH.L:HEALTH2 -0.51324 0.2413
PH.Q:HEALTH2 -0.51773 0.3162#homogeneity of variance assumption
## TURNS OUT THAT THERE IS NO EVIDENCE OF NON-HOMOGENEITY
library(nlme)
stehman.gls <- gls(BRATING~HEALTH*PH, data=stehman)
stehman.gls1 <- gls(BRATING~HEALTH*PH, data=stehman, weights=varIdent(form=~1|HEALTH*PH))
anova(stehman.gls, stehman.gls1) Model df AIC BIC logLik Test
stehman.gls 1 7 161.4 178.9 -73.72
stehman.gls1 2 12 167.1 196.9 -71.52 1 vs 2
L.Ratio p-value
stehman.gls
stehman.gls1 4.393 0.4944anova(stehman.gls,type="marginal")Denom. DF: 89
numDF F-value p-value
(Intercept) 1 127.25 <.0001
HEALTH 1 5.29 0.0238
PH 2 3.71 0.0283
HEALTH:PH 2 0.37 0.6897anova(stehman.gls1,type="marginal")Denom. DF: 89
numDF F-value p-value
(Intercept) 1 122.16 <.0001
HEALTH 1 6.05 0.0159
PH 2 4.03 0.0212
HEALTH:PH 2 0.43 0.6545quinn <- read.table('../data/quinn.csv', header=T, sep=',', strip.white=T)
head(quinn) SEASON DENSITY RECRUITS SQRTRECRUITS GROUP
1 Spring Low 15 3.873 SpringLow
2 Spring Low 10 3.162 SpringLow
3 Spring Low 13 3.606 SpringLow
4 Spring Low 13 3.606 SpringLow
5 Spring Low 5 2.236 SpringLow
6 Spring High 11 3.317 SpringHighpar(mfrow=c(1,2))
boxplot(RECRUITS~SEASON*DENSITY, data=quinn)
boxplot(sqrt(RECRUITS)~SEASON*DENSITY, data=quinn)
!is.list(replications(sqrt(RECRUITS)~SEASON*DENSITY,data=quinn))[1] FALSEreplications(sqrt(RECRUITS)~SEASON*DENSITY,data=quinn)$SEASON
SEASON
Autumn Spring Summer Winter
10 11 12 9
$DENSITY
DENSITY
High Low
24 18
$`SEASON:DENSITY`
DENSITY
SEASON High Low
Autumn 6 4
Spring 6 5
Summer 6 6
Winter 6 3#contrasts(quinn$SEASON) <- contr.sum
#contrasts(quinn$DENSITY) <- contr.sum
quinn.lm <- lm(SQRTRECRUITS~SEASON*DENSITY, data=quinn)
summary(quinn.lm)
Call:
lm(formula = SQRTRECRUITS ~ SEASON * DENSITY, data = quinn)
Residuals:
Min 1Q Median 3Q Max
-2.230 -0.598 0.138 0.549 1.886
Coefficients:
Estimate Std. Error
(Intercept) 4.230 0.412
SEASONSpring -1.210 0.583
SEASONSummer 2.636 0.583
SEASONWinter -1.957 0.583
DENSITYLow 0.030 0.652
SEASONSpring:DENSITYLow 0.247 0.894
SEASONSummer:DENSITYLow -2.243 0.875
SEASONWinter:DENSITYLow -1.360 0.967
t value Pr(>|t|)
(Intercept) 10.26 6.1e-12 ***
SEASONSpring -2.07 0.046 *
SEASONSummer 4.52 7.1e-05 ***
SEASONWinter -3.36 0.002 **
DENSITYLow 0.05 0.964
SEASONSpring:DENSITYLow 0.28 0.784
SEASONSummer:DENSITYLow -2.56 0.015 *
SEASONWinter:DENSITYLow -1.41 0.169
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.01 on 34 degrees of freedom
Multiple R-squared: 0.753, Adjusted R-squared: 0.702
F-statistic: 14.8 on 7 and 34 DF, p-value: 1.1e-08library(car)
with(quinn,interaction.plot(SEASON,DENSITY,SQRTRECRUITS))
summary(quinn.lm)
Call:
lm(formula = SQRTRECRUITS ~ SEASON * DENSITY, data = quinn)
Residuals:
Min 1Q Median 3Q Max
-2.230 -0.598 0.138 0.549 1.886
Coefficients:
Estimate Std. Error
(Intercept) 4.230 0.412
SEASONSpring -1.210 0.583
SEASONSummer 2.636 0.583
SEASONWinter -1.957 0.583
DENSITYLow 0.030 0.652
SEASONSpring:DENSITYLow 0.247 0.894
SEASONSummer:DENSITYLow -2.243 0.875
SEASONWinter:DENSITYLow -1.360 0.967
t value Pr(>|t|)
(Intercept) 10.26 6.1e-12 ***
SEASONSpring -2.07 0.046 *
SEASONSummer 4.52 7.1e-05 ***
SEASONWinter -3.36 0.002 **
DENSITYLow 0.05 0.964
SEASONSpring:DENSITYLow 0.28 0.784
SEASONSummer:DENSITYLow -2.56 0.015 *
SEASONWinter:DENSITYLow -1.41 0.169
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.01 on 34 degrees of freedom
Multiple R-squared: 0.753, Adjusted R-squared: 0.702
F-statistic: 14.8 on 7 and 34 DF, p-value: 1.1e-08levels(quinn$SEASON)[1] "Autumn" "Spring" "Summer" "Winter"summary(lm(SQRTRECRUITS~DENSITY, data=subset(quinn, SEASON=='Autumn')))
Call:
lm(formula = SQRTRECRUITS ~ DENSITY, data = subset(quinn, SEASON ==
"Autumn"))
Residuals:
Min 1Q Median 3Q Max
-2.2298 -0.5977 0.0976 0.4262 1.7702
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.230 0.480 8.81 2.2e-05
DENSITYLow 0.030 0.759 0.04 0.97
(Intercept) ***
DENSITYLow
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.18 on 8 degrees of freedom
Multiple R-squared: 0.000195, Adjusted R-squared: -0.125
F-statistic: 0.00156 on 1 and 8 DF, p-value: 0.969summary(lm(SQRTRECRUITS~DENSITY, data=subset(quinn, SEASON=='Spring')))
Call:
lm(formula = SQRTRECRUITS ~ DENSITY, data = subset(quinn, SEASON ==
"Spring"))
Residuals:
Min 1Q Median 3Q Max
-2.0200 0.0041 0.2967 0.4428 0.8530
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.020 0.359 8.42 1.5e-05
DENSITYLow 0.277 0.532 0.52 0.62
(Intercept) ***
DENSITYLow
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.878 on 9 degrees of freedom
Multiple R-squared: 0.0292, Adjusted R-squared: -0.0787
F-statistic: 0.27 on 1 and 9 DF, p-value: 0.616summary(lm(SQRTRECRUITS~DENSITY, data=subset(quinn, SEASON=='Summer')))
Call:
lm(formula = SQRTRECRUITS ~ DENSITY, data = subset(quinn, SEASON ==
"Summer"))
Residuals:
Min 1Q Median 3Q Max
-1.5741 -0.5348 0.0324 0.5456 1.4410
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.866 0.372 18.4 4.7e-09
DENSITYLow -2.213 0.527 -4.2 0.0018
(Intercept) ***
DENSITYLow **
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.912 on 10 degrees of freedom
Multiple R-squared: 0.639, Adjusted R-squared: 0.602
F-statistic: 17.7 on 1 and 10 DF, p-value: 0.00182summary(lm(SQRTRECRUITS~DENSITY, data=subset(quinn, SEASON=='Winter')))
Call:
lm(formula = SQRTRECRUITS ~ DENSITY, data = subset(quinn, SEASON ==
"Winter"))
Residuals:
Min 1Q Median 3Q Max
-1.2724 -0.9428 -0.0363 0.7276 1.8856
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.272 0.446 5.10 0.0014
DENSITYLow -1.330 0.772 -1.72 0.1288
(Intercept) **
DENSITYLow
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.09 on 7 degrees of freedom
Multiple R-squared: 0.297, Adjusted R-squared: 0.197
F-statistic: 2.96 on 1 and 7 DF, p-value: 0.129library(contrast)
contrast(quinn.lm, a=list(DENSITY='High', SEASON=levels(quinn$SEASON)),
b=list(DENSITY='Low', SEASON=levels(quinn$SEASON)))lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
-0.02996 0.6520 -1.3550 1.2950 -0.05 34 0.9636
-0.27653 0.6116 -1.5195 0.9664 -0.45 34 0.6540
2.21340 0.5832 1.0283 3.3985 3.80 34 0.0006
1.32959 0.7142 -0.1219 2.7810 1.86 34 0.0713library(car)
quinn.lm2 <- lm(sqrt(RECRUITS)~DENSITY*SEASON, data=quinn)
contrasts(quinn$SEASON) <- contr.sum
contrasts(quinn$DENSITY) <- contr.sum
quinn.lm2 <- lm(sqrt(RECRUITS)~DENSITY*SEASON, data=quinn)
library(car)
Anova(quinn.lm2, type="III")Anova Table (Type III tests)
Response: sqrt(RECRUITS)
Sum Sq Df F value Pr(>F)
(Intercept) 540 1 529.04 < 2e-16 ***
DENSITY 6 1 6.35 0.017 *
SEASON 91 3 29.61 1.3e-09 ***
DENSITY:SEASON 11 3 3.71 0.021 *
Residuals 35 34
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#library(biology)
#AnovaM(quinn.lm.summer <- mainEffects(quinn.lm2, at=SEASON=="Summer"), type="III")
#library(biology)
#AnovaM(quinn.lm. <- mainEffects(quinn.lm, at=SEASON=="Autumn"), type="III")
#AnovaM(quinn.lm. <- mainEffects(quinn.lm, at=SEASON=="Winter"), type="III")
#AnovaM(quinn.lm. <- mainEffects(quinn.lm, at=SEASON=="Spring"), type="III")
#Or via contrasts - not this is still in sqrt scale
#which are not trivial to reverse (due to negatives)
library(contrast)
quinn.contr<-contrast(quinn.lm, a=list(SEASON=levels(quinn$SEASON),DENSITY="High"), b=list(SEASON=levels(quinn$SEASON),DENSITY="Low"))
with(quinn.contr,data.frame(SEASON,Contrast,Lower,Upper,testStat,df,Pvalue)) SEASON Contrast Lower Upper testStat df
1 Autumn -0.02996 -1.3550 1.2950 -0.04595 34
2 Spring -0.27653 -1.5195 0.9664 -0.45214 34
3 Summer 2.21340 1.0283 3.3985 3.79557 34
4 Winter 1.32959 -0.1219 2.7810 1.86162 34
Pvalue
1 0.9636151
2 0.6540421
3 0.0005794
4 0.0713198#Or via contrasts
xmat <- with(quinn,expand.grid(SEASON=levels(SEASON),DENSITY=levels(DENSITY)))
contrasts(xmat$SEASON) <-"contr.sum"
contrasts(xmat$DENSITY) <-"contr.sum"
mm <- model.matrix(~SEASON*DENSITY, xmat)
mm.high <- mm[xmat$DENSITY=="High",]
mm.low <- mm[xmat$DENSITY=="Low",]
mm.density <- mm.high-mm.low
rownames(mm.density) <- levels(quinn$SEASON)
summary(glht(quinn.lm, mm.density))
Simultaneous Tests for General Linear Hypotheses
Fit: lm(formula = SQRTRECRUITS ~ SEASON * DENSITY, data = quinn)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
Autumn == 0 0.553 1.223 0.45 0.9834
Spring == 0 -4.427 1.166 -3.80 0.0023
Summer == 0 -2.659 1.428 -1.86 0.2451
Winter == 0 6.773 5.666 1.20 0.6460
Autumn == 0
Spring == 0 **
Summer == 0
Winter == 0
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)data.frame(confint(glht(quinn.lm, mm.density))$confint,SEASON=levels(quinn$SEASON)) Estimate lwr upr SEASON
Autumn 0.5531 -2.648 3.755 Autumn
Spring -4.4268 -7.479 -1.374 Spring
Summer -2.6592 -6.398 1.079 Summer
Winter 6.7726 -8.056 21.601 Winter