Frequentist vs Bayesian
|
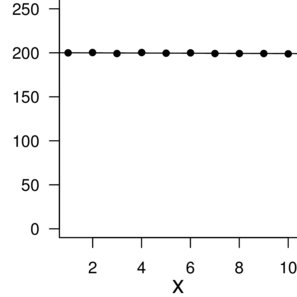
n: 10 |
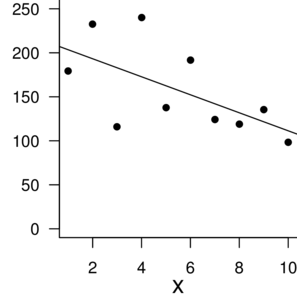
n: 10 |
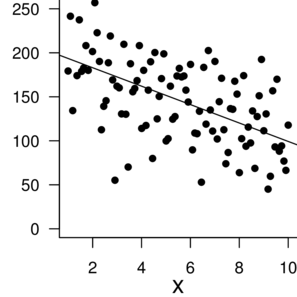
n: 100 |

- P(D|H)
- long-run frequency
- simple analytical methods to solve roots
- conclusions pertain to data, not parameters or hypotheses
- compared to theoretical distribution when NULL is true
- probability of obtaining observed data or MORE EXTREME data
- \(P(D|H)\)
- can a null ever actually be true
-------------------------------------------------
Frequentist Bayesian
-------------- ------------ ------------
Obs. data One possible Fixed, true
Parameters Fixed, true Random,
distribution
Inferences Data Parameters
Probability Long-run frequency Degree of belief
$P(D|H)$ $P(H|D)$
-------------------------------------------------


|
n: 10 |
n: 10 |
n: 100 |




| Population A | Population B | |
|---|---|---|
| Percentage change | 0.46 | 45.46 |
| Prob. >5% decline | 0 | 0.86 |
The normalizing constant is required for probability - turn a frequency distribution into a probability distribution
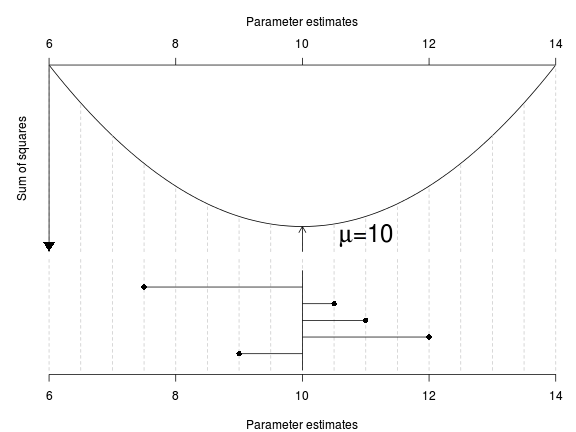

|
\(P(D|H)\) |
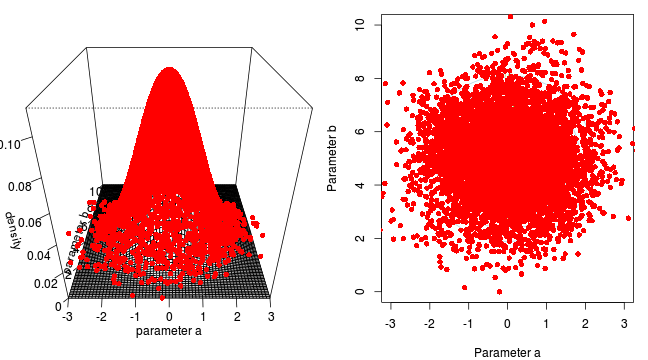
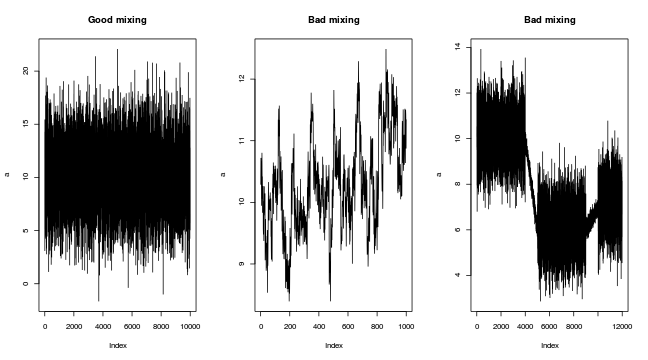
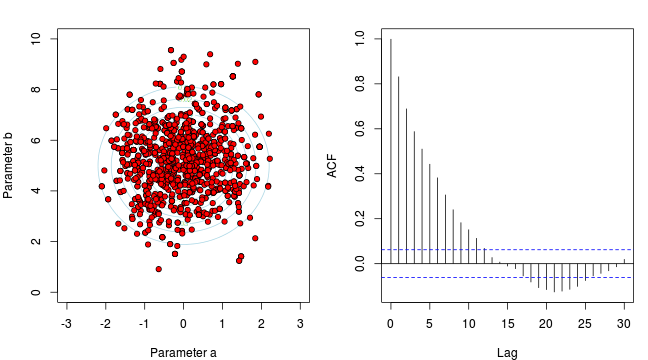
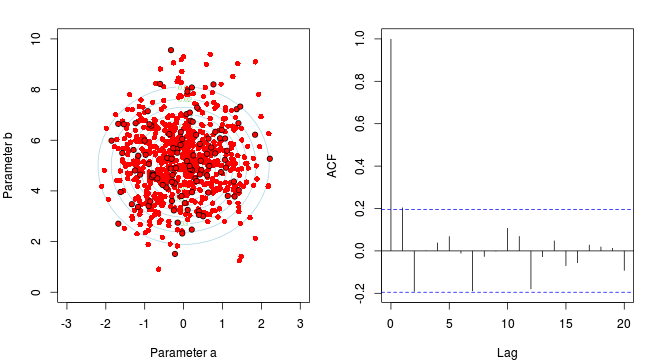
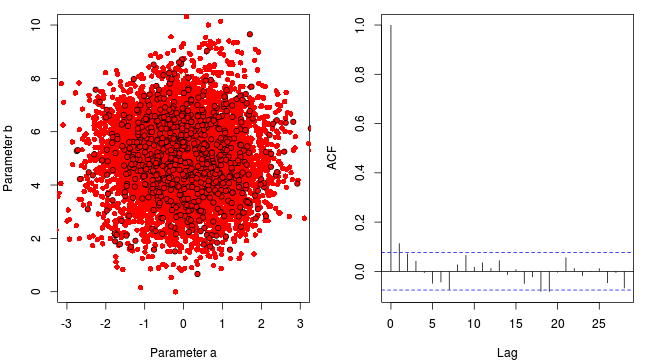
Marchov Chain Monte Carlo sampling

<ul>
<li>two parameters $\alpha$ and $\beta$</li>
<li>infinitely vague priors - posterior likelihood only</li>
<li>likelihood multivariate normal</li>Marchov Chain Monte Carlo sampling
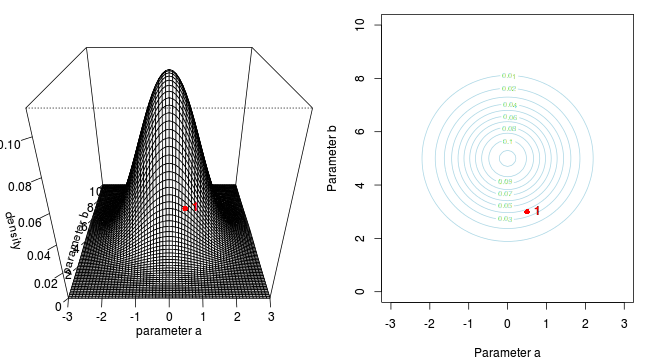
<ul>
<li>two parameters $\alpha$ and $\beta$</li>
<li>infinitely vague priors - posterior likelihood only</li>
<li>likelihood multivariate normal</li>Marchov Chain Monte Carlo sampling
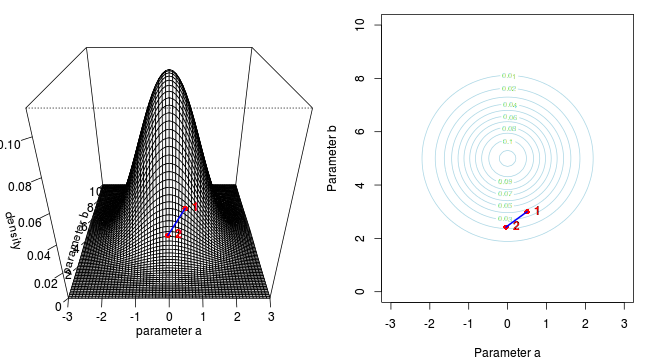
Marchov Chain Monte Carlo sampling
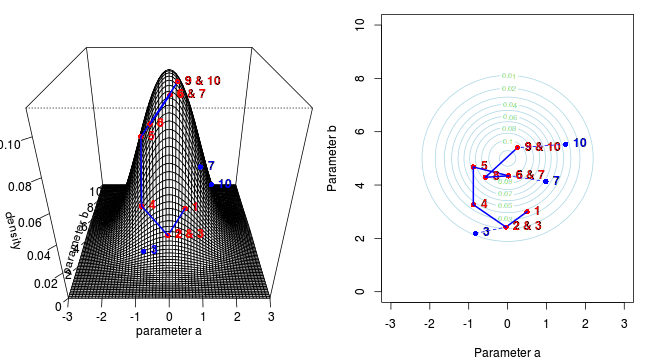
Marchov Chain Monte Carlo sampling
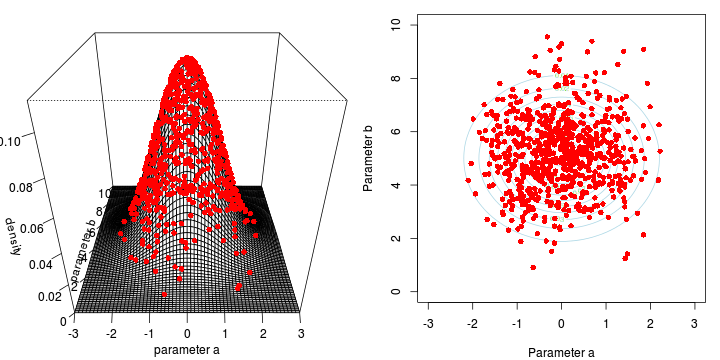
Marchov Chain Monte Carlo sampling
Marchov Chain Monte Carlo sampling

- \(y_i \sim{} N(\beta_0 + \beta_1 x_i, \sigma^2)\)
- \(y_i \sim{} N(\beta_0 + \beta_1 x_i, \tau)\)
- \(\tau\) is precision (\(\frac{1}{\sigma^2}\))- \(y_i \sim{} N(\mu_i, \tau)\)
\(\mu_i = \beta_0 + \beta_1 x_i\)
- \(\beta_0 \sim{} N(0,0.000001)\)
- \(\beta_1 \sim{} N(0,0.000001)\)
- \(\tau = \frac{1}{\sigma^2}\)
- \(\sigma \sim{} Uniform(0,100)\)
|
\(y_i \sim{} N(\mu_i, \tau)\) \(\mu_i = \beta_0 + \beta_1 x_i\) \(\beta_0 \sim{} N(0,0.000001)\) \(\beta_1 \sim{} N(0,0.000001)\) \(\tau = \frac{1}{\sigma^2}\) \(\sigma \sim{} Uniform(0,100)\) |
> writeLines(modelString,con="BUGSscripts/regression.txt")Error in file(con, "w"): cannot open the connection| Y | X |
|---|---|
| 3 | 0 |
| 2.5 | 1 |
| 6 | 2 |
| 5.5 | 3 |
| 9 | 4 |
| 8.6 | 5 |
| 12 | 6 |
Y X
1 3.0 0
2 2.5 1
3 6.0 2
4 5.5 3
5 9.0 4
6 8.6 5
7 12.0 6> data.list <- with(DATA,
+ list(y=Y,
+ x=X,n=nrow(DATA))
+ )
> data.list$y
[1] 3.0 2.5 6.0 5.5 9.0 8.6 12.0
$x
[1] 0 1 2 3 4 5 6
$n
[1] 7> #params <- c("beta0","beta1","sigma")
> #burnInSteps = 2000
> #nChains = 3
> #numSavedSteps = 50000
> #thinSteps = 1
> #nIter = ceiling((numSavedSteps * thinSteps)/nChains)> library(R2jags)