Tutorial 6.1 - Frequentist hypothesis testing (one and two populations)
15 May 2017
Hypothesis testing
Tutorial 4.1 illustrated how samples can be used to estimate numerical characteristics or parameters of populations. Recall that in a statistical context, the term population refers to all the possible observations of a particular condition from which samples are collected, and that this does not necessarily represent a biological population.
Importantly, recall that the standard error is an estimate of how variable repeated parameter estimates (e.g. population means) are likely to be from repeated (long-run) population re-sampling. Also recall, that the standard error can be estimated from a single collected sample given the degree of variability and size of this sample.
Hence, sample means allow us make inferences about the population means, and the strength of these inferences is determined by estimates of how precise (or repeatable) the estimated population means are likely to be (standard error). The concept of precision introduces the value of using the characteristics of a single sample to estimate the likely characteristics of repeated samples from a population. This same philosophy of estimating the characteristics of a large number of possible samples and outcomes forms the basis of frequentist approach to statistics in which samples are used to objectively test specific hypotheses about populations.
A biological or research hypothesis is a concise statement about the predicted or theorized nature of a population or populations and usually proposes that there is an effect of a treatment (e.g. the means of two populations are different). Logically however, theories (and thus hypothesis) cannot be proved, only disproved (falsification) and thus a null hypothesis ($H_0$) is formulated to represent all possibilities except the hypothesized prediction. For example, if the hypothesis is that there is a difference between (or relationship among) populations, then the null hypothesis is that there is no difference or relationship (effect). Evidence against the null hypothesis thereby provides evidence that the hypothesis is likely to be true.
The next step in hypothesis testing is to decide on an appropriate statistic that describes the nature of population estimates in the context of the null hypothesis taking into account the precision of estimates. For example, if the null hypothesis is that the mean of one population is different to the mean of another population, the null hypothesis is that the population means are equal. The null hypothesis can therefore be represented mathematically as: $H_0: \mu_1=\mu_2$ or equivalently: $H_0: \mu_1 - \mu_2 = 0$.
The appropriate test statistic for such a null hypothesis is a t-statistic: $$t = \frac{(\bar{y}_1 -\bar{y}_2) - (\mu_1 - \mu_2)}{s_{\bar{y}_1-\bar{y}_2}} = \frac{(\bar{y}_1 -\bar{y}_2)}{s_{\bar{y}_1-\bar{y}_2}}$$ where ($\bar{y}_1 -\bar{y}_2$) is the degree of difference between sample means of population 1 and 2 and $s_{\bar{y}_1-\bar{y}_2}$ expresses the level of precision in the difference.
If the null hypothesis is true and the two populations have identical means, we might expect that the means of samples collected from the two populations would be similar and thus the difference in means would be close to 0, as would the value of the t-statistic. Since populations and thus samples are variable, it is unlikely that two samples will have identical means, even if they are collected from identical populations (or the same population). Therefore, if the two populations were repeatedly sampled (with comparable collection technique and sample size) and t-statistics calculated, it would be expected that 50% of the time, the mean of sample 1 would be greater than that of population 2 and vice verse. Hence, 50% of the time, the value of the t-statistic would be greater than 0 and 50% of the time it would be less than 0. Furthermore, samples that are very different from one another (yielding large positive or negative t-values), although possible, would rarely be collected.
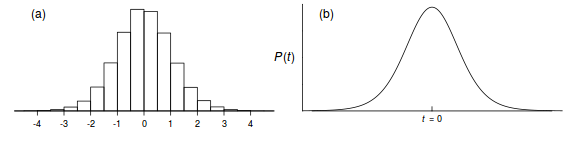
All the possible values of the t-statistic (and thus sample combinations) calculated for a specific sample size for the situation when the null hypothesis is true could be collated and a histogram generated (see Figure 1a). From a frequentist perspective, this represents the sampling or probability distribution for the t-statistic calculated from repeated samples of a specific sample size (degrees of freedom\index{S}{degrees of freedom}) collected under the situation when the null hypothesis is true. That is, it represents all the possible expected t-values we might expect when there is no effect. When certain conditions (assumptions) are met, these t-values follow a known distribution called a t-distribution (see Figure 1b) for which the exact mathematical formula is known. The area under the entire t-distribution (curve) is one, and thus, areas under regions of the curve can be calculated, which in turn represent the relative frequencies (probabilities) of obtaining t-values in those regions. From the above example, the probability (p-value) of obtaining a t-value of greater than zero when the null hypothesis is true (population means equal) is 0.5 (50%).
When real samples are collected from two populations, the null hypothesis that the two population means are equal is tested by calculating the real value of the t-statistic, and using an appropriate t-distribution to calculate the probability of obtaining the observed (data) t-value or ones more extreme when the null hypothesis is true. If this probability is very low (below a set critical value, typically 0.05 or 5%), it is unlikely that the sample(s) could have come from such population(s) and thus the null hypothesis is unlikely to be true. This then provides evidence that the hypothesis is true.
Similarly, all other forms of hypothesis testing follow the same principal. The value of a test statistic that has been calculated from collected data is compared to the appropriate probability distribution for that statistic. If the probability of obtaining the observed value of the test statistic (or ones more extreme) when the null hypothesis is true is less than a predefined critical value, the null hypothesis is rejected, otherwise it is not rejected.
Note that the probability distributions of test statistics are strictly defined under a specific set of conditions. For example, the t-distribution is calculated for theoretical populations that are exactly normal (see Tutorial 7) and of identical variability. The further the actual populations (and thus samples) deviate from these ideal conditions, the less reliably the theoretical probability distributions will approximate the actual distribution of possible values of the test statistic, and thus, the less reliable the resulting hypothesis test.
One and two-tailed tests
Two-tailed tests are any test used to test a null hypotheses that can be rejected by large deviations from expected in either direction. For example, when testing the null hypothesis that two population means are equal, the null hypothesis could be rejected if either population was greater than the other. By contrast one-tailed tests are those tests that are used to test more specific null hypotheses that restrict null hypothesis rejection to only outcomes in one direction. For example, we could use a one-tailed test to test the null hypothesis that the mean of population 1 was greater or equal to the mean of population 2. This null hypothesis would only be rejected if population 2 mean was significantly greater than that of population 1.
t-tests
Single population t-tests
Two population t-tests are used to test null hypotheses that two independent populations are equal with respect to some parameter (typically the mean, e.g. $H_0: \mu_1=\mu_2$). The t-test formula presented above is used in the original student or pooled variances t-test. The separate variances t-test (Welch's test), represents an improvement of the t-test in that more appropriately accomodates samples with modestly unequal variances.
Paired samples t-tests
When observations are collected from a population in pairs such that two variables are measured from each sampling unit, a paired t-test can be used to test the null hypothesis that the population mean difference between paired observations is equal to zero ($H_0: \mu_d=0$). Note that this is equivalent to a single population t-test testing a null hypotheses that the population parameter is equal to the specific value of zero.
Assumptions
The theoretical t-distributions were formulated for samples collected from theoretical populations that are:
- normally distributed
- equally varied
Although substantial deviations from normality and/or homogeneity of variance reduce the reliability of the t-distribution and thus p-values and conclusions, t-tests are reasonably robust to violations of normality and to a lesser degree, homogeneity of variance (provided sample sizes equal).
As with most hypothesis tests, t-tests also assume 3) that each of the observations are independent (or that pairs are independent of one another in the case of paired t-tests). If observations are not independent, then a sample may not be an unbiased representation of the entire population, and therefore any resulting analyses could completely misrepresent any biological effects.
Statistical decision and power
Recall that probability distributions are typically symmetrical, bell-shaped distributions that define the relative frequencies (probabilities) of all possible outcomes and suggest that progressively more extreme outcomes become progressively less frequent or likely. By convention however, the statistical criteria for any given hypothesis test is a watershed value typically set at 0.05 or 5%.
Belying the gradational decline in probabilities, outcomes with a probability less than 5% are considered unlikely whereas values equal to or greater are considered likely. However, values less than 5% are of course possible and could be obtained if the samples were by chance not centered similarly to the population(s) - that is, if the sample(s) were atypical of the population(s).
When rejecting a null hypothesis at the 5% level, we are therefore accepting that there is a 5% change that we are making an error (a Type I error)\index{S}{Type I error}. We are concluding that there is an effect or trend, yet it is possible that there really is no trend, we just had unusual samples. Conversely, when a null hypothesis is not rejected (probability of 5% or greater) even though there really is a trend or effect in the population, a Type II error has been committed. Hence a Type II error is when you fail to detect an effect that really occurs.
Since rejecting a null hypothesis is considered to be evidence of a hypothesis or theory and therefore scientific advancement, the scientific community projects itself against too many false rejections by keeping the statistical criteria and thus Type I error rate low (5%). However, as Type I and Type II error rates are linked, doing so leaves the Type II error rate ($\beta$) relatively large (approximately 20%).
The reciprocal of the Type II error rate, is called power\index{S}{power}. Power is the probability that a test will detect an effect (reject a null hypothesis, not make a Type II error) if one really occurs. Power is proportional to the statistical criteria, and thus lowering the statistical criteria compromises power. The conventional value of $\alpha=0.05$) represents a compromise between Type I error rate and power.
Power is also affected by other aspects of a research framework and can be described by the following general representation: $$power(1-\beta)\propto\frac{ES \sqrt{n}~\alpha}{\sigma}$$ Statistical power is:
- directly proportional to the effect size\index{S}{effect size ($ES$)} ($ES$) which is the absolute size or magnitude of the effect or trend in the population. The more subtle the difference or effect, the lower the power
- directly proportional to the sample size ($n$). The greater the sample size, the greater the power
- directly proportional to the significance level ($\alpha = 0.05$) as previously indicated
- inversely proportional to the population standard deviation ($\sigma$). The more variable the population, the lower the power
When designing an experiment or survey, a researcher would usually like to know how many replicates are going to be required. Consequently, the above relationship is often transposed to express it in terms of sample size for a given amount of power: $$n\propto\frac{(power~\sigma)^2}{ES~\alpha}$$ Researchers typically aim for power of at least 0.8 (80% probability of detecting an effect if one exists). Effect size and population standard deviation are derived from either pilot studies, previous research, documented regulations or gut feeling.
Robust tests
There are a number of more robust (yet less powerful) alternatives to independent samples t-tests and paired t-tests.
- The Mann-Whitney-Wilcoxon test is a non-parametric (rank-based) equivalent of the independent samples t-test that uses the ranks of the observations to calculate test statistics rather than the actual observations and tests the null hypothesis that the two sampled populations have equal distributions. The Mann-Whitney U-test and the Wilcoxon two-sample test are two computationally different tests that yield identical statistics.
- Similarly, the non-parametric Wilcoxon signed-rank test uses the sums of positive and negative signed ranked differences between paired observations to test the null hypothesis that the two sets of observations come from the one population. While neither test dictate that sampled populations must follow a specific distribution, the Wilcoxon signed-rank test does assume that the population differences are symmetrically distributed about the median and the Mann-Whitney test assumes that the sampled populations are equally varied (although violations of this assumption apparently have little impact).
- Randomization tests in which the factor levels are repeatedly shuffled so as to yield a probability distribution for the relevant statistic (such as the t-statistic) specific to the sample data do not have any distributional assumptions. Strictly however, randomization tests examine whether the sample patterns could have occurred by chance and do not pertain to populations.
