Tutorial 9.2b - Nested ANOVA (Bayesian)
23 Dec 2015
If you are completely ontop of the conceptual issues pertaining to Nested ANOVA, and just need to use this tutorial in order to learn about Nested ANOVA in R, you are invited to skip down to the section on Nested ANOVA in R.
Overview
You are strongly advised to review the information on the nested design in tutorial 9.2a. I am not going to duplicate the overview here.
Linear models
So called 'random effects' are modelled differently from 'fixed effects' in that rather than estimate their individual effects, we instead estimate the variability due to these 'random effects'. Since technically all variables in a Bayesian framework are random, some prefer to use the terms 'fixed effects' and 'varying effects'. As random factors typically represent 'random' selections of levels (such as a set of randomly selected sites), incorporated in order to account for the dependency structure (observations within sites are more likely to be correlated to one another - not strickly independent) to the data, we are not overly interested in the individual differences between levels of the 'varying' (random) factor. Instead (in addition to imposing a separate correlation structure within each nest), we want to know how much variability is attributed to this level of the design.
The linear models for two and three factor nested design are:
$$
\begin{align}
y_{ijk}&=\mu+\alpha_i + \beta_{j(i)} + \varepsilon_{ijk} &\hspace{2em} \varepsilon_{ijk}&\sim\mathcal{N}(0,\sigma^2), \hspace{1em}\beta_{j(i)}\sim\mathcal{N}(0,\sigma_B^2)\\
y_{ijkl}&=\mu+\alpha_i + \beta_{j(i)} + \gamma_{k(j(i))} + \varepsilon_{ijkl} &\hspace{2em} \varepsilon_{ijkl}&\sim\mathcal{N}(0,\sigma^2), \hspace{1em}\beta_{j(i)}\sim\mathcal{N}(0,\sigma_B^2), \hspace{1em}\gamma_{k(j(i))}\sim\mathcal{N}(0,\sigma_C^2)\\
\end{align}
$$
where $\mu$ is the overall mean, $\alpha$ is the effect of Factor A, $\beta$ is the variability of Factor B (nested within Factor A), $\gamma$ is the variability of Factor C (nested within Factor B) and $\varepsilon$ is the random unexplained or residual component that is assumed to be normally distributed with a mean of zero and a constant amount of standard deviation ($\sigma^2$).
The subscripts are iterators. For example, the $i$ represents the number of effects to be estimated for Factor A. Thus the first formula can be read as 'the $k$th observation of $y$ is drawn from a normal distribution (with a specific level of variability) and mean proposed to be determined by a base mean ($\mu$ - mean of the first treatment across all nests) plus the effect of the $i$th treatment effect plus the variability 'the model proposes that given a base mean ($\mu$) and knowing the effect of the $i$th treatment (factor A) and which of the $j$th nests within the treatment 'the $k$th observation from Block $j$ (factor B) within treatment effect
Variance components
As previously alluded to, it can often be useful to determine the relative contribution (to explaining the unexplained variability) of each of the factors as this provides insights into the variability at each different scales.
These contributions are known as Variance components and are estimates of the added variances due to each of the factors. For consistency with leading texts on this topic, I have included estimated variance components for various balanced nested ANOVA designs in the above table. However, variance components based on a modified version of the maximum likelihood iterative model fitting procedure (REML) is generally recommended as this accommodates both balanced and unbalanced designs.
While there are no numerical differences in the calculations of variance components for fixed and random factors, fixed factors are interpreted very differently and arguably have little biological meaning (other to infer relative contribution). For fixed factors, variance components estimate the variance between the means of the specific populations that are represented by the selected levels of the factor and therefore represent somewhat arbitrary and artificial populations. For random factors, variance components estimate the variance between means of all possible populations that could have been selected and thus represents the true population variance.
Assumptions
Consistent with the hierarchical nature of the design (in which the site means are the appropriate level of replication for the main treatments), it is important that diagnostics associated with each factor reflect this hierarchy. Hence, the replicates for the treatment effects are the site means, and the replicates of the sites are the quadrat means.
- All of the observations are independent - this must be addressed at the design and collection stages. Importantly, to be considered independent replicates, the replicates must be made at the same scale at which the treatment is applied. For example, if the experiment involves subjecting organisms housed in tanks to different water temperatures, then the unit of replication is the individual tanks not the individual organisms in the tanks. The individuals in a tank are strictly not independent with respect to the treatment.
- The response variable (and thus the residuals) should be normally distributed for each sampled populations (combination of factors). Boxplots of each treatment combination are useful for diagnosing major issues with normality.
- The response variable should be equally varied (variance should not be related to mean as these are supposed to be estimated separately) for each combination of treatments. Again, boxplots are useful.
Design balance
In a Bayesian framework, issues of design balance essentially evaporate.
Nested ANOVA in R
Scenario and Data
Imagine we has designed an experiment in which we intend to measure a response ($y$) to one of treatments (three levels; 'a1', 'a2' and 'a3'). The treatments occur at a spatial scale (over an area) that far exceeds the logistical scale of sampling units (it would take too long to sample at the scale at which the treatments were applied). The treatments occurred at the scale of hectares whereas it was only feasible to sample $y$ using 1m quadrats.
Given that the treatments were naturally occurring (such as soil type), it was not possible to have more than five sites of each treatment type, yet prior experience suggested that the sites in which you intended to sample were very uneven and patchy with respect to $y$.
In an attempt to account for this inter-site variability (and thus maximize the power of the test for the effect of treatment, you decided to employ a nested design in which 10 quadrats were randomly located within each of the five replicate sites per three treatments. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the number of treatments = 3
- the number of sites per treatment = 5
- the total number of sites = 15
- the sample size per treatment= 5
- the number of quadrats per site = 10
- the mean of the treatments = 40, 70 and 80 respectively
- the variability (standard deviation) between sites of the same treatment = 12
- the variability (standard deviation) between quadrats within sites = 5
library(plyr) set.seed(1) nTreat <- 3 nSites <- 15 nSitesPerTreat <- nSites/nTreat nQuads <- 10 site.sigma <- 12 sigma <- 5 n <- nSites * nQuads sites <- gl(n=nSites,k=nQuads, lab=paste0('S',1:nSites)) A <- gl(nTreat, nSitesPerTreat*nQuads, n, labels=c('a1','a2','a3')) a.means <- c(40,70,80) ## the site means (treatment effects) are drawn from normal distributions ## with means of 40, 70 and 80 and standard deviations of 12 A.effects <- rnorm(nSites, rep(a.means,each=nSitesPerTreat),site.sigma) #A.effects <- a.means %*% t(model.matrix(~A, data.frame(A=gl(nTreat,nSitesPerTreat,nSites))))+rnorm(nSites,0,site.sigma) Xmat <- model.matrix(~sites -1) lin.pred <- Xmat %*% c(A.effects) ## the quadrat observations (within sites) are drawn from ## normal distributions with means according to the site means ## and standard deviations of 5 y <- rnorm(n,lin.pred,sigma) data.nest <- data.frame(y=y, A=A, Sites=sites,Quads=1:length(y)) head(data.nest) #print out the first six rows of the data set
y A Sites Quads 1 32.25789 a1 S1 1 2 32.40160 a1 S1 2 3 37.20174 a1 S1 3 4 36.58866 a1 S1 4 5 35.45206 a1 S1 5 6 37.07744 a1 S1 6
library(ggplot2) ggplot(data.nest, aes(y=y, x=1)) + geom_boxplot() + facet_grid(.~Sites)
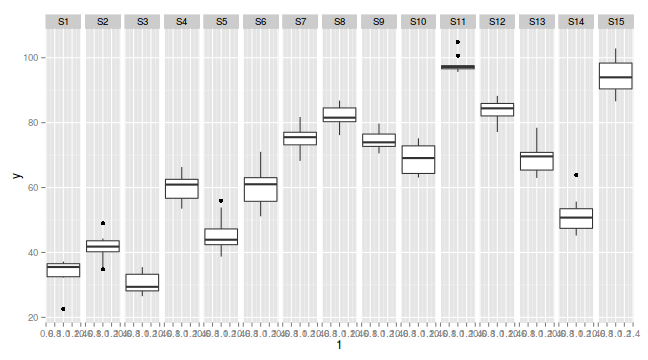
Exploratory data analysis
Normality and Homogeneity of variance
#Effects of treatment library(plyr) boxplot(y~A, ddply(data.nest, ~A+Sites,numcolwise(mean, na.rm=T)))
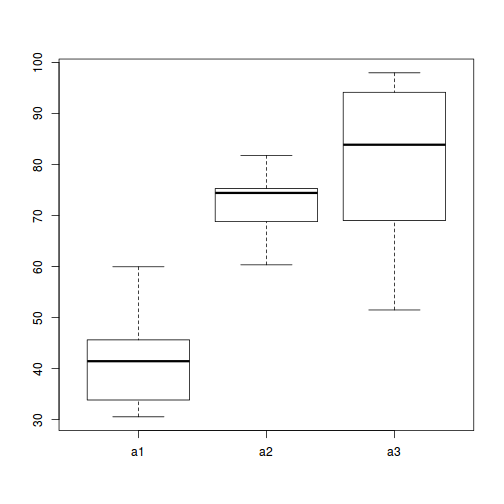
#Site effects boxplot(y~Sites, ddply(data.nest, ~A+Sites+Quads,numcolwise(mean, na.rm=T)))
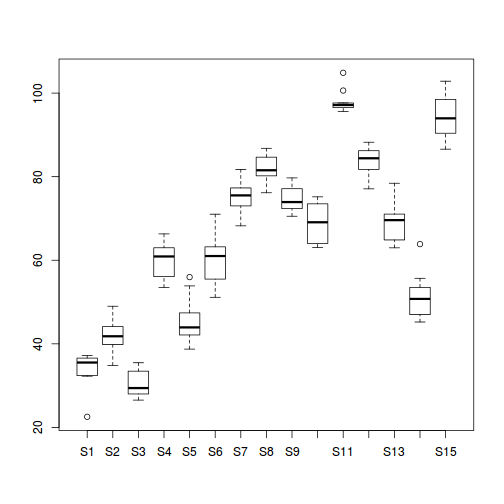
## with ggplot2 ggplot(ddply(data.nest, ~A+Sites,numcolwise(mean, na.rm=T)), aes(y=y, x=A)) + geom_boxplot()
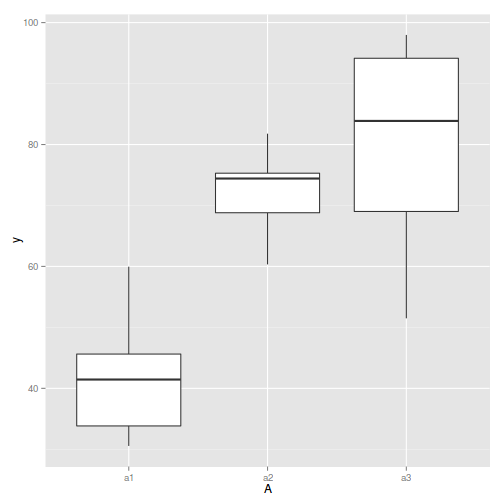
Conclusions:
- there is no evidence that the response variable is consistently non-normal across all populations - each boxplot is approximately symmetrical
- there is no evidence that variance (as estimated by the height of the boxplots) differs between the five populations. . More importantly, there is no evidence of a relationship between mean and variance - the height of boxplots does not increase with increasing position along the y-axis. Hence it there is no evidence of non-homogeneity
- transform the scale of the response variables (to address normality etc). Note transformations should be applied to the entire response variable (not just those populations that are skewed).
JAGS
For non-hierarchical linear models, uniform priors on variance (standard deviation) parameters seem to
work reasonably well.
Gelman (2006) warns that the use of the inverse-gamma family of non-informative
priors are very sensitive to $\epsilon$ particularly when variance is close to zero and this may lead to unintentionally
informative priors. When the number of groups (treatments or varying/random effects) is large (more than 5),
Gelman (2006) advocated the use of either uniform or half-cauchy priors. Yet when the
number of groups is low, Gelman (2006) indicates that uniform priors have a tendency
to result in inflated variance estimates. Consequently, half-cauchy priors are generally recommended for variances.
| Full parameterization | Matrix parameterization | Heirarchical parameterization |
|---|---|---|
| $$ \begin{array}{rcl} y_{ijk}&\sim&\mathcal{N}(\mu_{ij},\sigma^2)\\ \mu_{ij} &=& \alpha_0 + \alpha_{i} + \beta_{j(i)}\\ \beta_{i{j}}&\sim&\mathcal{N}(0,\sigma_{B}^2)\\ \alpha_0, \alpha_i&\sim&\mathcal{N}(0,100000)\\ \sigma^2, \sigma_{B}^2&\sim&\mathcal{Cauchy}(0,25)\\ \end{array} $$ | $$ \begin{array}{rcl} y_{ijk}&\sim&\mathcal{N}(\mu_{ij},\sigma^2)\\ \mu_{ij} &=& \alpha\mathbf{X} + \beta_{j(i)}\\ \beta_{i{j}}&\sim&\mathcal{N}(0,\sigma_{B}^2)\\ \alpha&\sim&\mathcal{MVN}(0,100000)\\ \sigma^2, \sigma_{B}^2&\sim&\mathcal{Cauchy}(0,25)\\ \end{array} $$ | $$ \begin{array}{rcl} y_{ij}&\sim &\mathcal{N}(\beta_{j(i)}, \sigma^2)\\ \beta_{j(i)}&\sim&\mathcal{N}(\mu_{i},\sigma_{B}^2)\\ \mu_{i}&=&\alpha\mathbf{X}\\ \alpha_i&\sim&\mathcal{N}(0, 1000000)\\ \sigma^2, \sigma_{B}^2&\sim&\mathcal{Cauchy}(0,25)\\ \end{array} $$ |
The full parameterization, shows the effects parameterization in which there is an intercept ($\alpha_0$) and two treatment effects ($\alpha_i$, where $i$ is 1,2).
The matrix parameterization is a compressed notation, In this parameterization, there are three alpha parameters (one representing the mean of treatment a1, and the other two representing the treatment effects (differences between a2 and a1 and a3 and a1). In generating priors for each of these three alpha parameters, we could loop through each and define a non-informative normal prior to each (as in the Full parameterization version). However, it turns out that it is more efficient (in terms of mixing and thus the number of necessary iterations) to define the priors from a multivariate normal distribution. This has as many means as there are parameters to estimate (3) and a 3x3 matrix of zeros and 100 in the diagonals. $$ \mu\sim\left[ \begin{array}{c} 0\\ 0\\ 0\\ \end{array} \right], \hspace{2em} \sigma^2\sim\left[ \begin{array}{ccc} 1000000&0&0\\ 0&1000000&0\\ 0&0&1000000\\ \end{array} \right] $$
In the Heirarchical parameterization, we are indicating two residual layers - one representing the variability in the observed data between individual observations (within sites) and the second representing the variability between site means (within the three treatments).
Full effects parameterization
modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha0 + alpha[A[i]] + beta[site[i]] } #Priors alpha0 ~ dnorm(0, 1.0E-6) alpha[1] <- 0 for (i in 2:nA) { alpha[i] ~ dnorm(0, 1.0E-6) #prior } for (i in 1:nSite) { beta[i] ~ dnorm(0, tau.B) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.B <- pow(sigma.B,-2) sigma.B <-z/sqrt(chSq.B) z.B ~ dnorm(0, .0016)I(0,) chSq.B ~ dgamma(0.5, 0.5) } " writeLines(modelString,con="../downloads/BUGSscripts/tut9.2bS3.1.f.txt")
data.nest.list <- with(data.nest, list(y=y, site=as.numeric(Sites), A=as.numeric(A), n=nrow(data.nest), nSite=length(levels(Sites)), nA = length(levels(A)) ) ) params <- c("alpha0","alpha","sigma","sigma.B") adaptSteps = 1000 burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] -0.5428819
jags.effects.f.time <- system.time( data.nest.r2jags.f <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/tut9.2bS3.1.f.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 503 Initializing model
jags.effects.f.time
user system elapsed 7.812 0.008 7.874
print(data.nest.r2jags.f)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.2bS3.1.f.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
alpha[2] 30.088 9.059 12.031 24.445 30.049 35.796 48.112 1.001 3000
alpha[3] 37.141 9.101 19.689 31.396 37.121 42.774 55.403 1.002 1700
alpha0 42.171 6.447 29.586 38.114 42.136 46.235 55.100 1.001 3000
sigma 4.428 0.273 3.940 4.241 4.415 4.598 4.996 1.001 3000
sigma.B 14.057 3.179 9.421 11.801 13.572 15.590 22.385 1.001 3000
deviance 869.642 6.183 859.552 865.156 868.846 873.323 883.745 1.002 1300
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 19.1 and DIC = 888.7
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.list.f <- as.mcmc(data.nest.r2jags.f)
[1] "alpha0" "alpha[1]" "alpha[2]" "alpha[3]" "deviance" "sigma" "sigma.B"
Matrix parameterization
modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- inprod(alpha[],X[i,]) + beta[site[i]] } #Priors alpha ~ dmnorm(a0,A0) for (i in 1:nSite) { beta[i] ~ dnorm(0, tau.B) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.B <- pow(sigma.B,-2) sigma.B <-z/sqrt(chSq.B) z.B ~ dnorm(0, .0016)I(0,) chSq.B ~ dgamma(0.5, 0.5) } " writeLines(modelString,con="../downloads/BUGSscripts/tut9.2bS3.1.m.txt")
A.Xmat <- model.matrix(~A,data.nest) data.nest.list <- with(data.nest, list(y=y, site=as.numeric(Sites), X=A.Xmat, n=nrow(data.nest), nSite=length(levels(Sites)), nA = ncol(A.Xmat), a0=rep(0,3), A0=diag(0,3) ) ) params <- c("alpha","sigma","sigma.B") adaptSteps = 1000 burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] 0.79071
jags.effects.m.time <- system.time( data.nest.r2jags.m <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/tut9.2bS3.1.m.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 965 Initializing model
jags.effects.m.time
user system elapsed 9.577 0.008 9.670
print(data.nest.r2jags.m)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.2bS3.1.m.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 42.362 6.448 29.963 38.129 42.351 46.617 54.771 1.003 900
alpha[2] 29.814 8.935 12.056 23.942 29.743 35.587 47.542 1.001 2300
alpha[3] 36.868 9.024 18.302 31.194 36.774 42.735 54.574 1.002 1400
sigma 4.431 0.270 3.945 4.242 4.417 4.603 5.009 1.001 2500
sigma.B 14.133 3.020 9.599 11.972 13.638 15.759 21.385 1.001 3000
deviance 869.516 5.925 860.027 865.256 868.874 873.104 882.656 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 17.6 and DIC = 887.1
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.list.m <- as.mcmc(data.nest.r2jags.m) Data.Nest.mcmc.list.m <- data.nest.mcmc.list.m
modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- inprod(alpha[],X[i,]) + inprod(beta[], Z[i,]) } #Priors alpha ~ dmnorm(a0,A0) for (i in 1:nZ) { beta[i] ~ dnorm(0, tau.B) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.B <- pow(sigma.B,-2) sigma.B <-z/sqrt(chSq.B) z.B ~ dnorm(0, .0016)I(0,) chSq.B ~ dgamma(0.5, 0.5) } "
A.Xmat <- model.matrix(~A,data.nest) Zmat <- model.matrix(~-1+Sites, data.nest) data.nest.list <- with(data.nest, list(y=y, X=A.Xmat, n=nrow(data.nest), Z=Zmat, nZ=ncol(Zmat), nA = ncol(A.Xmat), a0=rep(0,3), A0=diag(0,3) ) ) params <- c("alpha","sigma","sigma.B",'beta') burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] 0.3485099
jags.effects.m2.time <- system.time( data.nest.r2jags.m2 <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file=textConnection(modelString), n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 3231 Initializing model
jags.effects.m2.time
user system elapsed 16.541 0.016 16.755
print(data.nest.r2jags.m2)
Inference for Bugs model at "5", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 42.067 6.578 29.032 37.725 42.160 46.241 55.169 1.001 3000
alpha[2] 30.069 9.259 12.117 24.021 30.031 36.209 48.381 1.002 1800
alpha[3] 37.285 9.101 19.517 31.284 37.507 43.232 54.917 1.002 1500
beta[1] -8.128 6.675 -21.114 -12.440 -8.222 -3.889 4.897 1.001 3000
beta[2] -0.612 6.632 -13.657 -4.847 -0.702 3.688 12.406 1.001 3000
beta[3] -11.405 6.683 -24.807 -15.689 -11.483 -7.171 1.555 1.001 3000
beta[4] 17.700 6.673 4.694 13.437 17.662 22.145 31.058 1.001 3000
beta[5] 3.490 6.698 -9.694 -0.894 3.387 8.082 16.528 1.001 3000
beta[6] -11.674 6.603 -24.545 -15.902 -11.629 -7.462 1.011 1.002 1900
beta[7] 3.086 6.667 -9.762 -1.372 3.019 7.503 15.970 1.001 2300
beta[8] 9.543 6.607 -3.742 5.282 9.611 13.820 22.654 1.001 2500
beta[9] 2.287 6.676 -10.642 -2.088 2.300 6.640 15.307 1.001 2800
beta[10] -3.286 6.602 -16.114 -7.658 -3.222 0.915 9.541 1.001 2400
beta[11] 18.438 6.367 5.868 14.225 18.382 22.586 31.068 1.002 2000
beta[12] 4.476 6.433 -8.237 0.294 4.428 8.738 17.024 1.002 1600
beta[13] -10.203 6.400 -22.966 -14.385 -10.263 -6.120 2.182 1.002 1700
beta[14] -27.562 6.431 -40.197 -31.830 -27.430 -23.309 -14.994 1.002 1800
beta[15] 14.658 6.402 2.338 10.408 14.640 18.816 27.198 1.001 2300
sigma 4.424 0.271 3.933 4.237 4.410 4.599 5.003 1.001 3000
sigma.B 14.088 2.992 9.553 11.970 13.675 15.744 21.031 1.001 2800
deviance 869.547 6.092 859.967 865.210 868.616 873.111 883.730 1.002 2000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 18.5 and DIC = 888.1
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.list.m2 <- as.mcmc(data.nest.r2jags.m2) Data.Nest.mcmc.list.m2 <- data.nest.mcmc.list.m2
Hierarchical parameterization
modelString=" model { #Likelihood (esimating site means (gamma.site) for (i in 1:n) { y[i]~dnorm(quad.means[i],tau) quad.means[i] <- gamma.site[site[i]] } for (i in 1:s) { gamma.site[i] ~ dnorm(site.means[i], tau.site) site.means[i] <- inprod(beta[],A.Xmat[i,]) } #Priors for (i in 1:a) { beta[i] ~ dnorm(0, 1.0E-6) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.B <- pow(sigma.B,-2) sigma.B <-z/sqrt(chSq.B) z.B ~ dnorm(0, .0016)I(0,) chSq.B ~ dgamma(0.5, 0.5) tau.site <- pow(sigma.site,-2) sigma.site <-z/sqrt(chSq.site) z.site ~ dnorm(0, .0016)I(0,) chSq.site ~ dgamma(0.5, 0.5) } " writeLines(modelString,con="../downloads/BUGSscripts/tut9.2bS3.1.txt")
A.Xmat <- model.matrix(~A,ddply(data.nest,~Sites,catcolwise(unique))) data.nest.list <- with(data.nest, list(y=y, site=Sites, A.Xmat= A.Xmat, n=nrow(data.nest), s=length(levels(Sites)), a = ncol(A.Xmat) ) ) params <- c("beta","sigma","sigma.site") adaptSteps = 1000 burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] 0.3643516
jags.effects.simple.time <- system.time( data.nest.r2jags <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/tut9.2bS3.1.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 406 Initializing model
print(data.nest.r2jags)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.2bS3.1.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 42.291 6.619 29.102 38.006 42.265 46.554 55.150 1.001 3000
beta[2] 29.542 9.263 11.148 23.640 29.710 35.687 47.273 1.001 3000
beta[3] 36.933 9.273 18.407 31.142 36.908 42.774 54.705 1.001 3000
sigma 4.428 0.278 3.925 4.233 4.409 4.614 5.013 1.001 3000
sigma.site 14.137 3.079 9.566 11.986 13.642 15.762 21.504 1.001 3000
deviance 869.595 6.056 859.795 865.211 868.824 873.347 882.948 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 18.3 and DIC = 887.9
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.list <- as.mcmc(data.nest.r2jags)
modelString=" model { #Likelihood (esimating site means (gamma.site) for (i in 1:n) { y[i]~dnorm(quad.means[i],tau) quad.means[i] <- gamma.site[site[i]] y.err[i]<- quad.means[i]-y[i] } for (i in 1:s) { gamma.site[i] ~ dnorm(site.means[i], tau.site) site.means[i] <- inprod(beta[],A.Xmat[i,]) site.err[i] <- site.means[i] - gamma.site[i] } #Priors for (i in 1:a) { beta[i] ~ dnorm(0, 1.0E-6) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.site <- pow(sigma.site,-2) sigma.site <-z/sqrt(chSq.site) z.site ~ dnorm(0, .0016)I(0,) chSq.site ~ dgamma(0.5, 0.5) sd.y <- sd(y.err) sd.site <- sd(site.err) sd.A <- sd(beta) } " writeLines(modelString,con="../downloads/BUGSscripts/tut9.2bS3.1SD.txt")
A.Xmat <- model.matrix(~A,ddply(data.nest,~Sites,catcolwise(unique))) data.nest.list <- with(data.nest, list(y=y, site=Sites, A.Xmat= A.Xmat, n=nrow(data.nest), s=length(levels(Sites)), a = ncol(A.Xmat) ) ) params <- c("beta","sigma","sd.y",'sd.site','sd.A','sigma','sigma.site') adaptSteps = 1000 burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] 1.075778
jags.SD.time <- system.time( data.nest.r2jagsSD <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/tut9.2bS3.1SD.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 571 Initializing model
print(data.nest.r2jagsSD)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.2bS3.1SD.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 42.356 6.247 30.043 38.368 42.410 46.124 55.080 1.001 3000
beta[2] 29.793 8.891 11.548 24.253 29.953 35.495 47.365 1.001 3000
beta[3] 37.054 8.860 19.147 31.318 37.084 42.866 54.862 1.002 3000
sd.A 9.506 5.273 1.628 5.674 8.766 12.360 22.348 1.002 1400
sd.site 13.662 1.167 12.182 12.905 13.383 14.090 16.702 1.002 1500
sd.y 4.378 0.084 4.245 4.317 4.368 4.426 4.573 1.001 2600
sigma 4.429 0.276 3.949 4.230 4.414 4.605 5.013 1.001 3000
sigma.site 13.989 3.014 9.501 11.876 13.487 15.624 21.078 1.002 1700
deviance 869.639 6.104 859.832 865.322 868.942 873.053 883.310 1.001 2800
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 18.6 and DIC = 888.3
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.listSD <- as.mcmc(data.nest.r2jagsSD)
Rstan
Cell means parameterization
rstanString=" data{ int n; int nA; int nB; vector [n] y; int A[n]; int B[n]; } parameters{ real alpha[nA]; real<lower=0> sigma; vector [nB] beta; real<lower=0> sigma_B; } model{ real mu[n]; // Priors alpha ~ normal( 0 , 100 ); beta ~ normal( 0 , sigma_B ); sigma_B ~ cauchy( 0 , 25 ); sigma ~ cauchy( 0 , 25 ); for ( i in 1:n ) { mu[i] <- alpha[A[i]] + beta[B[i]]; } y ~ normal( mu , sigma ); } "
data.nest.list <- with(data.nest, list(y=y, A=as.numeric(A), B=as.numeric(Sites), n=nrow(data.nest), nB=length(levels(Sites)),nA=length(levels(A)))) burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.c.time <- system.time( data.nest.rstan.c <- stan(data=data.nest.list, model_code=rstanString, pars=c('alpha','sigma','sigma_B'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.41 seconds (Warm-up) # 5.4 seconds (Sampling) # 6.81 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.34 seconds (Warm-up) # 4.83 seconds (Sampling) # 6.17 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.3 seconds (Warm-up) # 5.41 seconds (Sampling) # 6.71 seconds (Total)
print(data.nest.rstan.c)
Inference for Stan model: rstanString.
3 chains, each with iter=13000; warmup=3000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha[1] 42.08 0.13 6.94 28.10 37.64 42.08 46.73 55.54 2721 1
alpha[2] 71.70 0.13 7.04 57.34 67.33 71.90 76.06 85.41 2929 1
alpha[3] 78.84 0.13 6.95 65.13 74.50 78.94 83.19 92.65 2829 1
sigma 4.41 0.01 0.27 3.92 4.23 4.40 4.59 4.95 2793 1
sigma_B 15.28 0.07 3.63 10.07 12.76 14.68 17.05 24.30 2715 1
lp__ -340.78 0.06 3.44 -348.51 -342.84 -340.33 -338.29 -335.37 2877 1
Samples were drawn using NUTS(diag_e) at Tue Jan 13 07:14:31 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest.rstan.c.df <-as.data.frame(extract(data.nest.rstan.c)) head(data.nest.rstan.c.df)
alpha.1 alpha.2 alpha.3 sigma sigma_B lp__ 1 49.61 76.03 68.16 4.713 13.83 -343.9 2 38.30 78.58 78.08 4.527 11.79 -340.6 3 49.83 73.75 79.77 4.872 12.61 -336.2 4 41.54 50.96 92.55 3.949 20.76 -342.8 5 33.08 69.08 84.15 4.101 14.88 -336.3 6 39.11 78.25 78.48 4.427 10.71 -342.1
data.nest.mcmc.c<-rstan:::as.mcmc.list.stanfit(data.nest.rstan.c) plyr:::adply(as.matrix(data.nest.rstan.c.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 alpha.1 42.08 9.533 37.639 42.08 46.729 75.866 28.980 56.283 35.90 48.855 2 alpha.2 71.90 44.736 67.325 71.90 76.061 103.790 57.346 85.439 65.43 78.292 3 alpha.3 78.94 48.500 74.501 78.94 83.189 108.715 64.980 92.419 72.22 85.211 4 sigma 4.40 3.621 4.228 4.40 4.585 5.835 3.904 4.927 4.10 4.626 5 sigma_B 14.68 7.428 12.757 14.68 17.055 34.375 9.190 22.720 11.18 17.284 6 lp__ -340.33 -355.469 -342.838 -340.33 -338.291 -332.218 -347.562 -334.755 -342.90 -336.451
Full effects parameterization
rstanString=" data{ int n; int nB; vector [n] y; int A2[n]; int A3[n]; int B[n]; } parameters{ real alpha0; real alpha2; real alpha3; real<lower=0> sigma; vector [nB] beta; real<lower=0> sigma_B; } model{ real mu[n]; // Priors alpha0 ~ normal( 0 , 100 ); alpha2 ~ normal( 0 , 100 ); alpha3 ~ normal( 0 , 100 ); beta ~ normal( 0 , sigma_B ); sigma_B ~ cauchy( 0 , 25 ); sigma ~ cauchy( 0 , 25 ); for ( i in 1:n ) { mu[i] <- alpha0 + alpha2*A2[i] + alpha3*A3[i] + beta[B[i]]; } y ~ normal( mu , sigma ); } "
A2 <- ifelse(data.nest$A=='a2',1,0) A3 <- ifelse(data.nest$A=='a3',1,0) data.nest.list <- with(data.nest, list(y=y, A2=A2, A3=A3, B=as.numeric(Sites), n=nrow(data.nest), nB=length(levels(Sites)))) burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps + ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.f.time <- system.time( data.nest.rstan.f <- stan(data=data.nest.list, model_code=rstanString, pars=c('alpha0','alpha2','alpha3','sigma','sigma_B'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 3.28 seconds (Warm-up) # 13.47 seconds (Sampling) # 16.75 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 3.48 seconds (Warm-up) # 14.72 seconds (Sampling) # 18.2 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 3.23 seconds (Warm-up) # 15.54 seconds (Sampling) # 18.77 seconds (Total)
print(data.nest.rstan.f)
Inference for Stan model: rstanString.
3 chains, each with iter=13000; warmup=3000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha0 42.45 0.13 6.93 29.24 37.94 42.50 46.83 56.15 2899 1
alpha2 29.58 0.18 9.82 10.24 23.39 29.53 35.72 49.69 2897 1
alpha3 36.83 0.18 9.50 17.37 30.62 37.07 42.96 55.63 2925 1
sigma 4.40 0.00 0.27 3.91 4.22 4.40 4.57 4.95 3000 1
sigma_B 14.95 0.07 3.50 9.95 12.52 14.35 16.77 23.11 2704 1
lp__ -340.59 0.07 3.34 -347.82 -342.64 -340.25 -338.20 -335.05 2584 1
Samples were drawn using NUTS(diag_e) at Mon May 4 09:23:09 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest.rstan.f.df <-as.data.frame(extract(data.nest.rstan.f)) head(data.nest.rstan.f.df)
alpha0 alpha2 alpha3 sigma sigma_B lp__ 1 32.47415 39.49903 40.69339 4.435729 13.640733 -339.0126 2 25.72473 49.36534 48.50811 4.599241 25.359650 -346.7289 3 55.57984 25.72382 44.14519 4.099557 19.877447 -343.5320 4 37.53338 32.71673 32.61893 4.619255 13.468995 -341.5376 5 43.42154 30.63651 33.91730 4.343031 9.067916 -340.4652 6 31.66594 50.17470 44.25908 3.999964 13.984926 -344.7312
data.nest.mcmc.f<-rstan:::as.mcmc.list.stanfit(data.nest.rstan.f) plyr:::adply(as.matrix(data.nest.rstan.f.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 alpha0 42.501846 6.911381 37.940547 42.501846 46.825055 73.056778 29.233689 56.14772 36.086736 49.269184 2 alpha2 29.531136 -1.666353 23.392484 29.531136 35.715508 69.217756 10.215123 49.68790 20.143402 38.562762 3 alpha3 37.071971 1.197981 30.623994 37.071971 42.958094 80.889476 18.257879 56.04997 28.298563 46.016004 4 sigma 4.396666 3.431330 4.218224 4.396666 4.574869 5.656815 3.875447 4.90624 4.119459 4.651383 5 sigma_B 14.349013 6.790137 12.516834 14.349013 16.766142 42.674970 9.345433 21.81630 11.270147 17.121305 6 lp__ -340.250078 -358.072758 -342.640643 -340.250078 -338.196360 -331.776385 -347.300454 -334.91509 -342.944121 -336.533948
Matrix parameterization
rstanString=" data{ int n; int nB; int nA; vector [n] y; matrix [n,nA] X; int B[n]; vector [nA] a0; matrix [nA,nA] A0; } parameters{ vector [nA] alpha; real<lower=0> sigma; vector [nB] beta; real<lower=0> sigma_B; } model{ real mu[n]; // Priors //alpha ~ normal( 0 , 100 ); alpha ~ multi_normal(a0,A0); beta ~ normal( 0 , sigma_B ); sigma_B ~ cauchy( 0 , 25); sigma ~ cauchy( 0 , 25 ); for ( i in 1:n ) { mu[i] <- dot_product(X[i],alpha) + beta[B[i]]; } y ~ normal( mu , sigma ); } "
X <- model.matrix(~A, data.nest) nA <- ncol(X) data.nest.list <- with(data.nest, list(y=y, X=X, B=as.numeric(Sites), n=nrow(data.nest), nB=length(levels(Sites)), nA=nA, a0=rep(0,nA), A0=diag(100000,nA))) burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.m.time <- system.time( data.nest.rstan.m <- stan(data=data.nest.list, model_code=rstanString, pars=c('alpha','sigma','sigma_B'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 4.55 seconds (Warm-up) # 16.06 seconds (Sampling) # 20.61 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 4.63 seconds (Warm-up) # 24.03 seconds (Sampling) # 28.66 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 4.26 seconds (Warm-up) # 22.02 seconds (Sampling) # 26.28 seconds (Total)
print(data.nest.rstan.m)
Inference for Stan model: rstanString.
3 chains, each with iter=13000; warmup=3000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha[1] 42.25 0.13 6.87 28.24 37.98 42.33 46.62 55.54 2790 1
alpha[2] 29.88 0.18 9.80 10.29 23.69 29.84 36.21 49.29 3000 1
alpha[3] 37.02 0.18 9.61 18.11 30.73 37.00 43.07 56.38 3000 1
sigma 4.41 0.00 0.27 3.92 4.23 4.39 4.59 4.95 3000 1
sigma_B 14.88 0.06 3.27 10.00 12.61 14.33 16.61 22.68 2740 1
lp__ -340.48 0.06 3.37 -347.89 -342.52 -340.18 -338.08 -334.84 2952 1
Samples were drawn using NUTS(diag_e) at Thu Feb 19 08:32:30 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest.rstan.m.df <-as.data.frame(extract(data.nest.rstan.m)) head(data.nest.rstan.m.df)
alpha.1 alpha.2 alpha.3 sigma sigma_B lp__ 1 37.90 35.27 38.67 4.306 12.75 -337.2 2 39.83 28.98 44.57 4.704 16.34 -337.6 3 47.66 18.27 41.29 4.575 10.54 -344.4 4 39.40 32.05 39.63 4.334 14.11 -337.9 5 44.49 34.05 37.88 4.588 15.83 -340.6 6 42.56 23.89 32.94 4.658 14.37 -339.4
data.nest.mcmc.m<-rstan:::as.mcmc.list.stanfit(data.nest.rstan.m) plyr:::adply(as.matrix(data.nest.rstan.m.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 alpha.1 42.331 15.703 37.976 42.331 46.616 70.261 28.782 55.863 36.425 49.449 2 alpha.2 29.843 -16.683 23.688 29.843 36.212 68.901 11.076 49.889 21.084 39.769 3 alpha.3 36.996 -5.127 30.726 36.996 43.066 80.704 17.129 55.169 26.566 44.635 4 sigma 4.394 3.617 4.226 4.394 4.589 5.455 3.890 4.916 4.146 4.672 5 sigma_B 14.327 7.738 12.613 14.327 16.608 38.417 9.569 21.283 11.197 16.928 6 lp__ -340.184 -354.122 -342.521 -340.184 -338.079 -332.052 -347.122 -334.425 -342.609 -336.099
Heirarchical parameterization
rstanString=" data{ int n; int nA; int nSites; vector [n] y; matrix [nSites,nA] X; matrix [n,nSites] Z; } parameters{ vector[nA] beta; vector[nSites] gamma; real<lower=0> sigma; real<lower=0> sigma_S; } model{ vector [n] mu_site; vector [nSites] mu; // Priors beta ~ normal( 0 , 1000 ); gamma ~ normal( 0 , 1000 ); sigma ~ cauchy( 0 , 25 ); sigma_S~ cauchy( 0 , 25 ); mu_site <- Z*gamma; y ~ normal( mu_site , sigma ); mu <- X*beta; gamma ~ normal(mu, sigma_S); } "
dt.A <- ddply(data.nest,~Sites,catcolwise(unique)) X<-model.matrix(~A, dt.A) Z<-model.matrix(~Sites-1, data.nest) data.nest.list <- list(y=data.nest$y, X=X, Z=Z, n=nrow(data.nest), nSites=nrow(X),nA=ncol(X)) burnInSteps = 2000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.time <- system.time( data.nest.rstan <- stan(data=data.nest.list, model_code=rstanString, pars=c('beta','sigma','sigma_S'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 12000 [ 0%] (Warmup) Iteration: 1200 / 12000 [ 10%] (Warmup) Iteration: 2001 / 12000 [ 16%] (Sampling) Iteration: 3200 / 12000 [ 26%] (Sampling) Iteration: 4400 / 12000 [ 36%] (Sampling) Iteration: 5600 / 12000 [ 46%] (Sampling) Iteration: 6800 / 12000 [ 56%] (Sampling) Iteration: 8000 / 12000 [ 66%] (Sampling) Iteration: 9200 / 12000 [ 76%] (Sampling) Iteration: 10400 / 12000 [ 86%] (Sampling) Iteration: 11600 / 12000 [ 96%] (Sampling) Iteration: 12000 / 12000 [100%] (Sampling) # Elapsed Time: 0.95 seconds (Warm-up) # 2.64 seconds (Sampling) # 3.59 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 12000 [ 0%] (Warmup) Iteration: 1200 / 12000 [ 10%] (Warmup) Iteration: 2001 / 12000 [ 16%] (Sampling) Iteration: 3200 / 12000 [ 26%] (Sampling) Iteration: 4400 / 12000 [ 36%] (Sampling) Iteration: 5600 / 12000 [ 46%] (Sampling) Iteration: 6800 / 12000 [ 56%] (Sampling) Iteration: 8000 / 12000 [ 66%] (Sampling) Iteration: 9200 / 12000 [ 76%] (Sampling) Iteration: 10400 / 12000 [ 86%] (Sampling) Iteration: 11600 / 12000 [ 96%] (Sampling) Iteration: 12000 / 12000 [100%] (Sampling) # Elapsed Time: 0.84 seconds (Warm-up) # 3.51 seconds (Sampling) # 4.35 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 12000 [ 0%] (Warmup) Iteration: 1200 / 12000 [ 10%] (Warmup) Iteration: 2001 / 12000 [ 16%] (Sampling) Iteration: 3200 / 12000 [ 26%] (Sampling) Iteration: 4400 / 12000 [ 36%] (Sampling) Iteration: 5600 / 12000 [ 46%] (Sampling) Iteration: 6800 / 12000 [ 56%] (Sampling) Iteration: 8000 / 12000 [ 66%] (Sampling) Iteration: 9200 / 12000 [ 76%] (Sampling) Iteration: 10400 / 12000 [ 86%] (Sampling) Iteration: 11600 / 12000 [ 96%] (Sampling) Iteration: 12000 / 12000 [100%] (Sampling) # Elapsed Time: 0.9 seconds (Warm-up) # 2.06 seconds (Sampling) # 2.96 seconds (Total)
print(data.nest.rstan)
Inference for Stan model: rstanString.
3 chains, each with iter=12000; warmup=2000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta[1] 42.25 0.13 6.89 28.35 37.88 42.33 46.61 56.50 3000 1
beta[2] 29.71 0.18 9.71 9.95 23.67 29.72 35.90 48.92 3000 1
beta[3] 36.93 0.18 9.79 17.08 30.50 36.93 43.37 56.33 3000 1
sigma 4.42 0.01 0.28 3.92 4.22 4.40 4.60 5.00 3000 1
sigma_S 14.78 0.06 3.34 9.90 12.32 14.21 16.68 22.71 2720 1
lp__ -340.53 0.06 3.40 -348.18 -342.64 -340.13 -338.06 -334.94 2912 1
Samples were drawn using NUTS(diag_e) at Thu Feb 19 08:35:35 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest.rstan.df <-as.data.frame(extract(data.nest.rstan)) head(data.nest.rstan.df)
beta.1 beta.2 beta.3 sigma sigma_S lp__ 1 52.90 5.691 20.97 4.830 17.77 -343.7 2 40.98 18.733 49.22 4.913 18.30 -341.5 3 41.67 26.881 44.36 4.762 10.83 -341.9 4 43.24 28.760 43.06 4.190 14.72 -338.7 5 43.28 26.365 33.50 4.821 13.97 -343.7 6 49.65 27.695 28.97 4.356 13.20 -337.1
data.nest.mcmc<-rstan:::as.mcmc.list.stanfit(data.nest.rstan) plyr:::adply(as.matrix(data.nest.rstan.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 beta.1 42.328 14.535 37.88 42.328 46.611 72.173 26.915 54.617 36.422 49.209 2 beta.2 29.722 -4.106 23.67 29.722 35.901 77.658 9.729 48.599 20.820 39.048 3 beta.3 36.929 -4.409 30.50 36.929 43.372 80.227 15.942 55.042 27.826 46.240 4 sigma 4.399 3.504 4.22 4.399 4.601 5.586 3.924 4.995 4.127 4.666 5 sigma_S 14.214 6.880 12.32 14.214 16.675 36.266 9.141 21.190 11.013 16.944 6 lp__ -340.126 -362.898 -342.64 -340.126 -338.062 -331.824 -347.103 -334.244 -343.293 -336.816
rstanString=" data{ int n; int nA; int nSites; vector [n] y; matrix [nSites,nA] X; matrix [n,nSites] Z; } parameters{ vector[nA] beta; vector[nSites] gamma; real<lower=0> sigma; real<lower=0> sigma_S; } model{ vector [n] mu_site; vector [nSites] mu; // Priors beta ~ normal( 0 , 1000 ); gamma ~ normal( 0 , 1000 ); sigma ~ cauchy( 0 , 25 ); sigma_S~ cauchy( 0 , 25 ); mu_site <- Z*gamma; y ~ normal( mu_site , sigma ); mu <- X*beta; gamma ~ normal(mu, sigma_S); } generated quantities { vector [n] mu_site; vector [nSites] mu; vector [n] y_err; real sd_y; vector [nSites] mu_site_err; real sd_site; real sd_A; mu_site <- Z*gamma; y_err <- mu_site - y; sd_y <- sd(y_err); mu <- X*beta; mu_site_err <- mu - gamma; sd_site <- sd(mu_site_err); sd_A <- sd(beta); } "
Unlike JAGS, STAN's var() and sd() functions generate sample variance and standard deviation rather than population versions. Therefore, it is arguably better to calculate the population standard deviations within R from the MCMC samples.
dt.A <- ddply(data.nest,~Sites,catcolwise(unique)) X<-model.matrix(~A, dt.A) Z<-model.matrix(~Sites-1, data.nest) data.nest.list <- list(y=data.nest$y, X=X, Z=Z, n=nrow(data.nest), nSites=nrow(X),nA=ncol(X)) burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.SD.time <- system.time( data.nest.rstanSD <- stan(data=data.nest.list, model_code=rstanString, pars=c('beta','sigma','sigma_S','sd_A','sd_site','sd_y'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.93 seconds (Warm-up) # 2.78 seconds (Sampling) # 3.71 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.1 seconds (Warm-up) # 2.41 seconds (Sampling) # 3.51 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.1 seconds (Warm-up) # 2.78 seconds (Sampling) # 3.88 seconds (Total)
print(data.nest.rstanSD)
Inference for Stan model: rstanString.
3 chains, each with iter=13000; warmup=3000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta[1] 42.45 0.12 6.79 29.16 38.09 42.59 46.72 55.80 3000 1
beta[2] 29.81 0.18 9.63 10.51 23.40 30.04 35.83 49.00 2983 1
beta[3] 36.85 0.18 9.92 17.03 30.62 36.70 43.05 57.03 2956 1
sigma 4.42 0.00 0.27 3.93 4.24 4.41 4.60 4.99 3000 1
sigma_S 14.86 0.06 3.36 9.95 12.51 14.35 16.56 22.89 3000 1
sd_A 10.08 0.10 5.71 1.76 5.89 9.22 13.28 23.94 3000 1
sd_site 13.84 0.03 1.40 12.28 12.95 13.47 14.32 17.49 3000 1
sd_y 4.38 0.00 0.09 4.25 4.32 4.37 4.43 4.58 3000 1
lp__ -340.57 0.06 3.48 -348.45 -342.70 -340.19 -338.04 -334.92 2999 1
Samples were drawn using NUTS(diag_e) at Thu Feb 19 08:38:26 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest.rstanSD.df <-as.data.frame(extract(data.nest.rstanSD)) head(data.nest.rstanSD.df)
beta.1 beta.2 beta.3 sigma sigma_S sd_A sd_site sd_y lp__ 1 37.64 25.04 40.55 4.460 16.63 8.243 13.51 4.312 -339.3 2 44.09 27.15 46.35 4.285 12.53 10.494 13.41 4.381 -339.2 3 33.73 41.89 40.89 3.930 12.94 4.448 13.10 4.355 -339.4 4 38.87 35.00 53.61 4.660 14.70 9.819 14.91 4.507 -344.8 5 51.41 15.90 31.59 4.721 16.01 17.793 13.59 4.519 -344.3 6 43.91 28.03 46.14 4.502 11.50 9.876 13.56 4.620 -349.1
data.nest.mcmcSD<-rstan:::as.mcmc.list.stanfit(data.nest.rstanSD) plyr:::adply(as.matrix(data.nest.rstanSD.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 beta.1 42.591 12.20757 38.093 42.591 46.722 67.341 28.7291 55.362 36.310 49.262 2 beta.2 30.043 -4.91213 23.402 30.043 35.833 64.149 11.0105 49.425 21.078 39.443 3 beta.3 36.697 -11.13186 30.624 36.697 43.054 97.367 16.7544 56.529 27.205 45.229 4 sigma 4.413 3.64025 4.241 4.413 4.595 5.439 3.9266 4.984 4.148 4.682 5 sigma_S 14.354 7.91922 12.510 14.354 16.561 37.159 9.0999 21.175 11.008 16.666 6 sd_A 9.219 0.09577 5.891 9.219 13.279 41.432 0.4164 20.659 3.394 13.617 7 sd_site 13.469 11.50089 12.947 13.469 14.320 28.962 12.0590 16.688 12.408 14.202 8 sd_y 4.366 4.18990 4.316 4.366 4.429 4.775 4.2227 4.540 4.276 4.433 9 lp__ -340.193 -356.63993 -342.696 -340.193 -338.037 -331.919 -347.2215 -334.098 -343.133 -336.460
$R^2$ and finite population standard deviations
modelString=" model { #Likelihood (esimating site means (gamma.site) for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- gamma[site[i]] + inprod(beta[], X[i,]) y.err[i]<- mu[i]-y[i] } #Priors for (i in 1:nSite) { gamma[i] ~ dnorm(0, tau.site) } beta ~ dmnorm(a0,A0) tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.site <- pow(sigma.site,-2) sigma.site <-z/sqrt(chSq.site) z.site ~ dnorm(0, .0016)I(0,) chSq.site ~ dgamma(0.5, 0.5) sd.y <- sd(y.err) sd.site <- sd(gamma) } "
A.Xmat <- model.matrix(~A,data.nest) nX=ncol(A.Xmat) data.nest.list <- with(data.nest, list(y=y, site=Sites, X= A.Xmat, n=nrow(data.nest), nSite=length(levels(Sites)), nX = ncol(A.Xmat), a0=rep(0,nX), A0=diag(1.0E-06,nX) ) ) params <- c("beta","sigma","sd.y",'sd.site','sigma','sigma.site') burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) jags.SD.time <- system.time( data.nest.r2jagsSD <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file=textConnection(modelString), n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 1119 Initializing model
jags.SD.time
user system elapsed 9.312 0.000 9.410
print(data.nest.r2jagsSD)
Inference for Bugs model at "5", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 42.493 6.446 29.226 38.399 42.479 46.558 55.119 1.001 3000
beta[2] 29.601 9.213 11.098 23.494 29.794 35.416 48.199 1.001 3000
beta[3] 36.647 8.929 19.397 30.733 36.608 42.360 53.886 1.008 3000
sd.site 13.691 1.216 12.243 12.905 13.378 14.139 16.829 1.001 3000
sd.y 4.378 0.084 4.249 4.315 4.368 4.427 4.580 1.001 3000
sigma 4.425 0.278 3.922 4.230 4.408 4.603 4.993 1.001 2800
sigma.site 14.029 2.986 9.526 11.930 13.601 15.633 21.261 1.001 3000
deviance 869.638 6.133 859.900 865.166 868.939 873.287 883.840 1.001 2100
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 18.8 and DIC = 888.4
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.listSD <- as.mcmc(data.nest.r2jagsSD) Xmat <- model.matrix(~A, data.nest) coefs <- data.nest.r2jagsSD$BUGSoutput$sims.list[['beta']] fitted <- coefs %*% t(Xmat) X.var <- aaply(fitted,1,function(x){var(x)}) Z.var <- data.nest.r2jagsSD$BUGSoutput$sims.list[['sd.site']]^2 R.var <- data.nest.r2jagsSD$BUGSoutput$sims.list[['sd.y']]^2 R2.marginal <- (X.var)/(X.var+Z.var+R.var) R2.marginal <- data.frame(Mean=mean(R2.marginal), Median=median(R2.marginal), HPDinterval(as.mcmc(R2.marginal))) R2.conditional <- (X.var+Z.var)/(X.var+Z.var+R.var) R2.conditional <- data.frame(Mean=mean(R2.conditional), Median=median(R2.conditional), HPDinterval(as.mcmc(R2.conditional))) R2.site <- (Z.var)/(X.var+Z.var+R.var) R2.site <- data.frame(Mean=mean(R2.site), Median=median(R2.site), HPDinterval(as.mcmc(R2.site))) R2.res<-(R.var)/(X.var+Z.var+R.var) R2.res <- data.frame(Mean=mean(R2.res), Median=median(R2.res), HPDinterval(as.mcmc(R2.res))) rbind(R2.site=R2.site, R2.marginal=R2.marginal, R2.res=R2.res, R2.conditional=R2.conditional)
Mean Median lower upper R2.site 0.40513614 0.37777481 0.26346438 0.62477617 R2.marginal 0.55316849 0.58096881 0.31506217 0.70640681 R2.res 0.04169536 0.04165901 0.02314323 0.06005702 R2.conditional 0.95830464 0.95834099 0.93994298 0.97685677
Graphical summary
newdata <- with(data.nest, data.frame(A=levels(A))) Xmat <- model.matrix(~A, newdata) coefs <- data.nest.r2jags.m$BUGSoutput$sims.list[['alpha']] fit <- coefs %*% t(Xmat) newdata <- cbind(newdata, adply(fit, 2, function(x) { data.frame(Mean=mean(x), Median=median(x), HPDinterval(as.mcmc(x)), HPDinterval(as.mcmc(x), p=0.68)) }) ) library(ggplot2) library(gridExtra) library(grid) p1 <- ggplot(newdata, aes(y=Median, x=A)) + geom_errorbar(aes(ymin=lower, ymax=upper), width=0.01, size=1) + geom_errorbar(aes(ymin=lower.1, ymax=upper.1), width=0, size=2) + geom_point(size=4, shape=21, fill='white')+ scale_y_continuous('Y')+ scale_x_discrete('X')+ theme_classic()+ theme(axis.title.y=element_text(vjust=2, size=rel(1.25)), axis.title.x=element_text(vjust=-2, size=rel(1.25)), plot.margin=unit(c(0.5,0.5,2,2), 'lines') ) data.nest.mcmc.listSD <- as.mcmc(data.nest.r2jagsSD) Xmat <- model.matrix(~A, data.nest) coefs <- data.nest.r2jagsSD$BUGSoutput$sims.list[['beta']] fitted <- coefs %*% t(Xmat) X.var <- aaply(fitted,1,function(x){var(x)}) Z.var <- data.nest.r2jagsSD$BUGSoutput$sims.list[['sd.site']]^2 R.var <- data.nest.r2jagsSD$BUGSoutput$sims.list[['sd.y']]^2 R2.marginal <- (X.var)/(X.var+Z.var+R.var) R2.marginal <- data.frame(Mean=mean(R2.marginal), Median=median(R2.marginal), HPDinterval(as.mcmc(R2.marginal))) R2.conditional <- (X.var+Z.var)/(X.var+Z.var+R.var) R2.conditional <- data.frame(Mean=mean(R2.conditional), Median=median(R2.conditional), HPDinterval(as.mcmc(R2.conditional))) R2.site <- (Z.var)/(X.var+Z.var+R.var) R2.site <- data.frame(Mean=mean(R2.site), Median=median(R2.site), HPDinterval(as.mcmc(R2.site))) R2.res<-(R.var)/(X.var+Z.var+R.var) R2.res <- data.frame(Mean=mean(R2.res), Median=median(R2.res), HPDinterval(as.mcmc(R2.res))) curdies.R2<-rbind(R2.site=R2.site, R2.marginal=R2.marginal, R2.res=R2.res, R2.conditional=R2.conditional) curdies.R2$name <- factor(rownames(curdies.R2), levels=c('R2.conditional','R2.res','R2.site','R2.marginal'), labels=c('Total','Residuals','Sites','A')) #curdies.R2$Perc <- curdies.R2$median/sum(curdies.R2$median) head(curdies.R2)
Mean Median lower upper name R2.site 0.40513614 0.37777481 0.26346438 0.62477617 Sites R2.marginal 0.55316849 0.58096881 0.31506217 0.70640681 A R2.res 0.04169536 0.04165901 0.02314323 0.06005702 Residuals R2.conditional 0.95830464 0.95834099 0.93994298 0.97685677 Total
p2<-ggplot(curdies.R2,aes(y=name, x=Median))+ geom_vline(xintercept=0,linetype="dashed")+ geom_hline(xintercept=0)+ #scale_x_continuous("Finite population \nvariance components (sd)")+ #geom_errorbarh(aes(xmin=lower.1, xmax=upper.1), height=0, size=1)+ geom_errorbarh(aes(xmin=lower, xmax=upper), height=0, size=1.5)+ geom_point(size=3, shape=21, fill='white')+ # geom_text(aes(label=sprintf("(%4.1f%%)",Perc),vjust=-1))+ theme_classic()+ theme(axis.title.y=element_blank(), axis.text.y=element_text(size=rel(1.2),hjust=1), axis.title.x=element_text(vjust=-2, size=rel(1.25)), plot.margin=unit(c(0.5,0.5,2,2), 'lines')) grid.arrange(p1,p2,nrow=1)
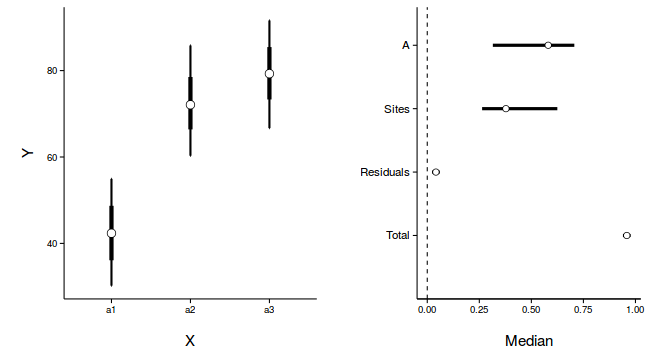
BRMS (STAN)
library(brms) data.nest.brm <- brm(y~A+(1|Sites), data=data.nest, family='gaussian', prior=c(set_prior('normal(0,100)', class='b'), set_prior('cauchy(0,5)', class='sd')), n.chains=3, n.iter=2000, warmup=500, n.thin=2 )
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Chain 1, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 1, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 1, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 1, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 1, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 1, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 1, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 1, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 1, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 1, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 1, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 1, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 1.72613 seconds (Warm-up) # 2.79666 seconds (Sampling) # 4.52279 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Chain 2, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 2, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 2, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 2, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 2, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 2, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 2, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 2, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 2, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 2, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 2, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 2, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 1.53597 seconds (Warm-up) # 2.79055 seconds (Sampling) # 4.32652 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Chain 3, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 3, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 3, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 3, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 3, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 3, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 3, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 3, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 3, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 3, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 3, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 3, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 1.22493 seconds (Warm-up) # 2.90738 seconds (Sampling) # 4.13231 seconds (Total)
summary(data.nest.brm)
Family: gaussian (identity)
Formula: y ~ A + (1 | Sites)
Data: data.nest (Number of observations: 150)
Samples: 3 chains, each with n.iter = 2000; n.warmup = 500; n.thin = 2;
total post-warmup samples = 2250
WAIC: 885.4
Random Effects:
~Sites (Number of levels: 15)
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sd(Intercept) 13.95 2.77 9.58 20.23 840 1.01
Fixed Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept 41.92 6.30 29.52 54.55 759 1
Aa2 30.28 8.85 12.40 47.54 780 1
Aa3 37.38 9.14 19.16 55.96 731 1
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sigma(y) 4.4 0.27 3.9 4.95 1178 1
Samples were drawn using NUTS(diag_e). For each parameter, Eff.Sample is a
crude measure of effective sample size, and Rhat is the potential scale
reduction factor on split chains (at convergence, Rhat = 1).
brms:::stancode(data.nest.brm)
functions {
}
data {
int<lower=1> N; # number of observations
vector[N] Y; # response variable
int<lower=1> K; # number of fixed effects
matrix[N, K] X; # FE design matrix
# data for random effects of Sites
int<lower=1> J_1[N]; # RE levels
int<lower=1> N_1; # number of levels
int<lower=1> K_1; # number of REs
real Z_1[N]; # RE design matrix
}
transformed data {
}
parameters {
real b_Intercept; # fixed effects Intercept
vector[K] b; # fixed effects
vector[N_1] pre_1; # unscaled REs
real<lower=0> sd_1; # RE standard deviation
real<lower=0> sigma; # residual SD
}
transformed parameters {
vector[N] eta; # linear predictor
vector[N_1] r_1; # REs
# compute linear predictor
eta <- X * b + b_Intercept;
r_1 <- sd_1 * (pre_1); # scale REs
# if available add REs to linear predictor
for (n in 1:N) {
eta[n] <- eta[n] + Z_1[n] * r_1[J_1[n]];
}
}
model {
# prior specifications
b_Intercept ~ normal(0,100);
b ~ normal(0,100);
sd_1 ~ cauchy(0,5);
pre_1 ~ normal(0, 1);
sigma ~ cauchy(0, 21);
# likelihood contribution
Y ~ normal(eta, sigma);
}
generated quantities {
}
#brms:::standata(data.nest.brm)
Quick glance Bayesian regression model specification
| JAGS Full | JAGS Matrix | JAGS heirarchy | Stan Cellmeans | Stan Full | Stan Matrix | Stan hierarcical | |
|---|---|---|---|---|---|---|---|
| Iterations | 13000 | 13000 | 13000 | 13000 | 13000 | 13000 | 12000 |
| Thinning | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Samples | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 |
| Maximum ACF | 0.0189 | 0.0169 | 0.0202 | 0.0531 | 0.0524 | 0.0462 | 0.0301 |
| Intercept | 42.14 [29.91 , 55.39] | 42.35 [30.22 , 54.94] | 42.27 [29.01 , 54.92] | 42.08 [28.98 , 56.28] | 42.50 [29.23 , 56.15] | 42.33 [28.78 , 55.86] | 42.33 [26.92 , 54.62] |
| alpha2 | 30.05 [12.79 , 48.63] | 29.74 [13.51 , 48.63] | 29.71 [10.96 , 46.82] | 71.90 [57.35 , 85.44] | 29.53 [10.22 , 49.69] | 29.84 [11.08 , 49.89] | 29.72 [9.73 , 48.60] |
| alpha3 | 37.12 [19.56 , 55.19] | 36.77 [18.30 , 54.57] | 36.91 [19.19 , 55.24] | 78.94 [64.98 , 92.42] | 37.07 [18.26 , 56.05] | 37.00 [17.13 , 55.17] | 36.93 [15.94 , 55.04] |
| sigma | 4.41 [3.93 , 4.99] | 4.42 [3.91 , 4.97] | 4.41 [3.90 , 4.98] | 4.40 [3.90 , 4.93] | 4.40 [3.88 , 4.91] | 4.39 [3.89 , 4.92] | 4.40 [3.92 , 5.00] |
| sigma.site | 13.57 [8.75 , 20.17] | 13.64 [8.87 , 19.75] | 13.64 [8.92 , 20.20] | 14.68 [9.19 , 22.72] | 14.35 [9.35 , 21.82] | 14.33 [9.57 , 21.28] | 14.21 [9.14 , 21.19] |
| Time (user self) | 7.81 | 9.58 | 6.92 | 19.92 | 53.48 | 75.70 | 11.11 |
| Time (system self) | 0.01 | 0.01 | 0.01 | 0.01 | 0.57 | 0.04 | 0.02 |
| Time (elapsed) | 7.87 | 9.67 | 6.94 | 53.43 | 86.65 | 105.92 | 38.84 |
| Time (user child) | 0.00 | 0.00 | 0.00 | 33.03 | 29.31 | 28.77 | 26.60 |
| Time (system child) | 0.00 | 0.00 | 0.00 | 0.82 | 0.99 | 0.66 | 0.76 |
| Model | JAGS | rstan |
|---|---|---|
| Full effects parameterization |
model {
#Likelihood
for (i in 1:n) {
y[i]~dnorm(mu[i],tau)
mu[i] <- alpha0 + alpha[A[i]] + beta.site[site[i]] + beta.quad[quad[i]]
}
#Priors
alpha0 ~ dnorm(0, 1.0E-6)
alpha[1] <- 0
for (i in 2:nA) {
alpha[i] ~ dnorm(0, 1.0E-6) #prior
}
for (i in 1:nSite) {
beta.site[i] ~ dnorm(0, tau.Bs) #prior
}
for (i in 1:nQuad) {
beta.quad[i] ~ dnorm(0, tau.Bq) #prior
}
tau <- pow(sigma,-2)
sigma <-z/sqrt(chSq)
|
data{
int n;
int nB;
vector [n] y;
int A2[n];
int A3[n];
int B[n];
}
parameters{
real alpha0;
real alpha2;
real alpha3;
real<lower=0> sigma;
vector [nB] beta;
real<lower=0> sigma_B;
}
model{
real mu[n];
// Priors
alpha0 ~ normal( 0 , 100 );
alpha2 ~ normal( 0 , 100 );
alpha3 ~ normal( 0 , 100 );
beta ~ normal( 0 , sigma_B );
sigma_B ~ cauchy( 0 , 25 );
sigma ~ cauchy( 0 , 25 );
for ( i in 1:n ) {
mu[i] <- alpha0 + alpha2*A2[i] +
alpha3*A3[i] + beta[B[i]];
}
y ~ normal( mu , sigma );
|
| Matrix parameterization |
data{
int n;
int nB;
int nA;
vector [n] y;
matrix [n,nA] X;
int B[n];
vector [nA] a0;
matrix [nA,nA] A0;
}
parameters{
vector [nA] alpha;
real<lower=0> sigma;
vector [nB] beta;
real<lower=0> sigma_B;
}
model{
real mu[n];
// Priors
//alpha ~ normal( 0 , 100 );
alpha ~ multi_normal(a0,A0);
beta ~ normal( 0 , sigma_B );
sigma_B ~ cauchy( 0 , 25);
sigma ~ cauchy( 0 , 25 );
for ( i in 1:n ) {
mu[i] <- dot_product(X[i],alpha) + beta[B[i]];
}
|
|
| Hierarchical parameterization |
data{
int n;
int nA;
int nSites;
vector [n] y;
matrix [nSites,nA] X;
matrix [n,nSites] Z;
}
parameters{
vector[nA] beta;
vector[nSites] gamma;
real<lower=0> sigma;
real<lower=0> sigma_S;
}
model{
vector [n] mu_site;
vector [nSites] mu;
// Priors
beta ~ normal( 0 , 1000 );
gamma ~ normal( 0 , 1000 );
sigma ~ cauchy( 0 , 25 );
sigma_S~ cauchy( 0 , 25 );
mu_site <- Z*gamma;
y ~ normal( mu_site , sigma );
mu <- X*beta;
gamma ~ normal(mu, sigma_S);
}
|
|
| Including finite-population standard deviations |
data{
int n;
int nA;
int nSites;
vector [n] y;
matrix [nSites,nA] X;
matrix [n,nSites] Z;
}
parameters{
vector[nA] beta;
vector[nSites] gamma;
real<lower=0> sigma;
real<lower=0> sigma_S;
}
model{
vector [n] mu_site;
vector [nSites] mu;
// Priors
beta ~ normal( 0 , 1000 );
gamma ~ normal( 0 , 1000 );
sigma ~ cauchy( 0 , 25 );
sigma_S~ cauchy( 0 , 25 );
mu_site <- Z*gamma;
y ~ normal( mu_site , sigma );
mu <- X*beta;
gamma ~ normal(mu, sigma_S);
}
generated quantities {
vector [n] mu_site;
vector [nSites] mu;
vector [n] y_err;
real sd_y;
vector [nSites] mu_site_err;
real sd_site;
real sd_A;
mu_site <- Z*gamma;
y_err <- mu_site - y;
sd_y <- sd(y_err);
mu <- X*beta;
mu_site_err <- mu - gamma;
sd_site <- sd(mu_site_err);
sd_A <- sd(beta);
}
|
Scenario and Data
Now imagine a similar experiment in which we intend to measure a response ($y$) to one of treatments (three levels; 'a1', 'a2' and 'a3'). As with the previous design, we decided to establish a nested design in which there are sub-replicate (1m Quadrats) within each Site.
In the current design, we have decided to further sub-replicate. Within each of the 5 Quadrats, we are going to randomly place 2x10cm pit traps. Now we have Sites nested within Treatments, Quadrats nested within Sites AND, Pits nested within Sites. The latter of these (Pits nested within Sites) are the observations ($y$). As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the number of treatments = 3
- the number of sites per treatment = 5
- the total number of sites = 15
- the number of quadrats per site = 5
- the number of pits per quadrat = 2
- the mean of the treatments = 40, 70 and 80 respectively
- the variability (standard deviation) between sites of the same treatment = 15
- the variability (standard deviation) between quadrats within sites = 10
- the variability (standard deviation) between pits within quadrats = 5
set.seed(3) nTreat <- 3 nSites <- 15 nSitesPerTreat <- nSites/nTreat nQuads <- 5 nPits <- 2 site.sigma <- 10 # sd within between sites within treatment quad.sigma <- 10 sigma <- 7.5 n <- nSites * nQuads * nPits sites <- gl(n=nSites,n/nSites,n, lab=paste("site",1:nSites)) A <- gl(nTreat, n/nTreat, n, labels=c('a1','a2','a3')) a.means <- c(40,70,80) #A<-gl(nTreat,nSites/nTreat,nSites,labels=c('a1','a2','a3')) a<-gl(nTreat,1,nTreat,labels=c('a1','a2','a3')) a.X <- model.matrix(~a, expand.grid(a)) a.eff <- as.vector(solve(a.X,a.means)) site.means <- rnorm(nSites,a.X %*% a.eff,site.sigma) A <- gl(nTreat,nSites/nTreat,nSites,labels=c('a1','a2','a3')) A.X <- model.matrix(~A, expand.grid(A)) #a.X <- model.matrix(~A, expand.grid(A=gl(nTreat,nSites/nTreat,nSites,labels=c('a1','a2','a3')))) site.means <- rnorm(nSites,A.X %*% a.eff,site.sigma) SITES <- gl(nSites,(nSites*nQuads)/nSites,nSites*nQuads,labels=paste('site',1:nSites)) sites.X <- model.matrix(~SITES-1) quad.means <- rnorm(nSites*nQuads,sites.X %*% site.means,quad.sigma) #SITES <- gl(nSites,1,nSites,labels=paste('site',1:nSites)) #sites.X <- model.matrix(~SITES-1) #quad.means <- rnorm(nSites*nQuads,sites.X %*% site.means,quad.sigma) QUADS <- gl(nSites*nQuads,n/(nSites*nQuads),n,labels=paste('quad',1:(nSites*nQuads))) quads.X <- model.matrix(~QUADS-1) #quads.eff <- as.vector(solve(quads.X,quad.means)) #pit.means <- rnorm(n,quads.eff %*% t(quads.X),sigma) pit.means <- rnorm(n,quads.X %*% quad.means,sigma) PITS <- gl(nPits*nSites*nQuads,1, n, labels=paste('pit',1:(nPits*nSites*nQuads))) data.nest1<-data.frame(Pits=PITS,Quads=QUADS,Sites=rep(SITES,each=2), A=rep(A,each=nQuads*nPits),y=pit.means) #data.nest1<-data.nest1[order(data.nest1$A,data.nest1$Sites,data.nest1$Quads),] head(data.nest1) #print out the first six rows of the data set
Pits Quads Sites A y 1 pit 1 quad 1 site 1 a1 50.49094 2 pit 2 quad 1 site 1 a1 47.48020 3 pit 3 quad 2 site 1 a1 31.20819 4 pit 4 quad 2 site 1 a1 40.32177 5 pit 5 quad 3 site 1 a1 47.81063 6 pit 6 quad 3 site 1 a1 40.72785
library(ggplot2) ggplot(data.nest1, aes(y=y, x=1)) + geom_boxplot() + facet_grid(.~Quads)
comparisonTab <- NULL
Exploratory data analysis
Normality and Homogeneity of variance
#Effects of treatment library(plyr) boxplot(y~A, ddply(data.nest1, ~A+Sites,numcolwise(mean, na.rm=T)))
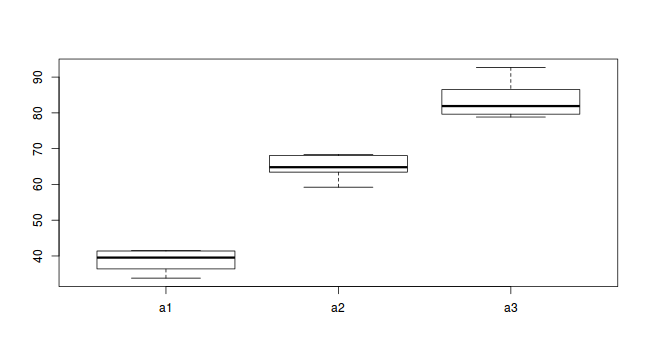
#Site effects boxplot(y~Sites, ddply(data.nest1, ~A+Sites+Quads,numcolwise(mean, na.rm=T)))
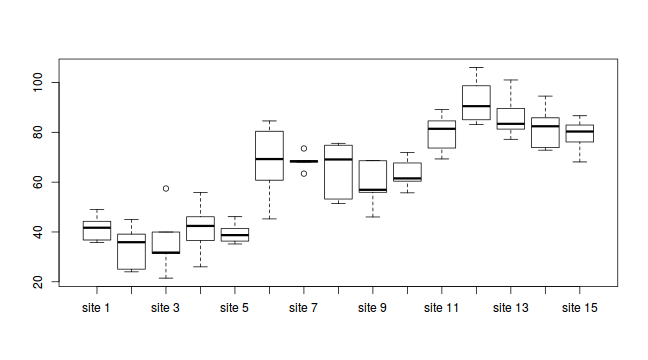
#Quadrat effects boxplot(y~Quads, ddply(data.nest1, ~A+Sites+Quads+Pits,numcolwise(mean, na.rm=T)))
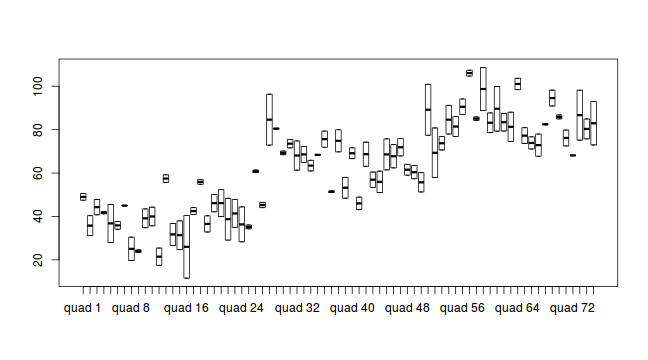
Conclusions:
- there is no evidence that the response variable is consistently non-normal across all populations - each boxplot is approximately symmetrical
- there is no evidence that variance (as estimated by the height of the boxplots) differs between the five populations. . More importantly, there is no evidence of a relationship between mean and variance - the height of boxplots does not increase with increasing position along the y-axis. Hence it there is no evidence of non-homogeneity
- It is a little difficult to assess normality/homogeneity of variance of quadrats since there are only two pits per quadrat. Nevertheless, there is no suggestion that variance increases with increasing mean.
- transform the scale of the response variables (to address normality etc). Note transformations should be applied to the entire response variable (not just those populations that are skewed).
Model fitting and analysis
Frequentist for comparison
d.lme <- lme(y ~ A, random=~1|Sites/Quads,data=data.nest1) summary(d.lme)
Linear mixed-effects model fit by REML
Data: data.nest1
AIC BIC logLik
1121.485 1139.428 -554.7426
Random effects:
Formula: ~1 | Sites
(Intercept)
StdDev: 1.234023
Formula: ~1 | Quads %in% Sites
(Intercept) Residual
StdDev: 7.747375 7.691963
Fixed effects: y ~ A
Value Std.Error DF t-value p-value
(Intercept) 38.52608 1.971994 75 19.536610 0
Aa2 26.26055 2.788821 12 9.416361 0
Aa3 45.38929 2.788821 12 16.275441 0
Correlation:
(Intr) Aa2
Aa2 -0.707
Aa3 -0.707 0.500
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.4234805 -0.6546746 0.0229929 0.6038953 2.3642962
Number of Observations: 150
Number of Groups:
Sites Quads %in% Sites
15 75
anova(d.lme)
numDF denDF F-value p-value (Intercept) 1 75 3004.7576 <.0001 A 2 12 133.5349 <.0001
JAGS
Full effects parameterization
modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha0 + alpha[A[i]] + beta.site[site[i]] + beta.quad[quad[i]] } #Priors alpha0 ~ dnorm(0, 1.0E-6) alpha[1] <- 0 for (i in 2:nA) { alpha[i] ~ dnorm(0, 1.0E-6) #prior } for (i in 1:nSite) { beta.site[i] ~ dnorm(0, tau.Bs) #prior } for (i in 1:nQuad) { beta.quad[i] ~ dnorm(0, tau.Bq) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.Bs <- pow(sigma.Bs,-2) sigma.Bs <-z/sqrt(chSq.Bs) z.Bs ~ dnorm(0, .0016)I(0,) chSq.Bs ~ dgamma(0.5, 0.5) tau.Bq <- pow(sigma.Bq,-2) sigma.Bq <-z/sqrt(chSq.Bq) z.Bq ~ dnorm(0, .0016)I(0,) chSq.Bq ~ dgamma(0.5, 0.5) } "
data.nest.list <- with(data.nest1, list(y=y, site=as.numeric(Sites), A=as.numeric(A), n=nrow(data.nest1), nSite=length(levels(Sites)), nA = length(levels(A)), nQuad=length(levels(Quads)), quad = as.numeric(Quads) ) ) params <- c("alpha0","alpha","sigma","sigma.Bs","sigma.Bq") burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] -1.724368
jags.effects.f.time <- system.time( data.nest.r2jags.f <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file=textConnection(modelString), #"../downloads/BUGSscripts/tut9.2bS3.1.f.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 794 Initializing model
jags.effects.f.time
user system elapsed 14.141 0.028 14.467
print(data.nest.r2jags.f)
Inference for Bugs model at "5", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
alpha[2] 26.208 3.516 19.144 23.893 26.263 28.520 32.944 1.001 3000
alpha[3] 45.358 3.493 38.522 43.116 45.359 47.545 52.567 1.003 810
alpha0 38.566 2.480 33.653 36.959 38.551 40.148 43.349 1.001 3000
sigma 7.830 0.669 6.664 7.378 7.786 8.229 9.303 1.001 2700
sigma.Bq 7.416 1.107 5.291 6.708 7.411 8.117 9.659 1.008 640
sigma.Bs 3.335 1.441 1.017 2.299 3.201 4.159 6.533 1.019 130
deviance 1042.256 18.611 1009.985 1029.121 1040.833 1053.745 1081.947 1.003 1200
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 173.0 and DIC = 1215.3
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest.mcmc.list.f <- as.mcmc(data.nest.r2jags.f)
Matrix parameterization
Note, in JAGS, this is substantially slower than the full effects model listed above...modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- inprod(alpha[], X[i,]) + inprod(beta.site[],Z.site[i,]) + inprod(beta.quad[],Z.quad[i,]) y.err[i] <- y[i]-mu[i] } #Priors for (i in 1:nX) { alpha[i] ~ dnorm(0, 1.0E-6) #prior } for (i in 1:nSite) { beta.site[i] ~ dnorm(0, tau.Bs) #prior } for (i in 1:nQuad) { beta.quad[i] ~ dnorm(0, tau.Bq) #prior } tau <- pow(sigma,-2) sigma <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.Bs <- pow(sigma.Bs,-2) sigma.Bs <-z/sqrt(chSq.Bs) z.Bs ~ dnorm(0, .0016)I(0,) chSq.Bs ~ dgamma(0.5, 0.5) tau.Bq <- pow(sigma.Bq,-2) sigma.Bq <-z/sqrt(chSq.Bq) z.Bq ~ dnorm(0, .0016)I(0,) chSq.Bq ~ dgamma(0.5, 0.5) sd.res <- sd(y.err[]) sd.site <- sd(beta.site[]) sd.quad <- sd(beta.quad[]) } "
Xmat <- model.matrix(~A, data=data.nest1) Zsite <- model.matrix(~-1+Sites, data=data.nest1) Zquad <- model.matrix(~-1+Quads, data=data.nest1) data.nest.list <- with(data.nest1, list(y=y, n=nrow(data.nest1), X=Xmat, nX=ncol(Xmat), Z.site=Zsite, nSite=ncol(Zsite), Z.quad=Zquad, nQuad=ncol(Zquad) ) ) params <- c("alpha0","alpha","sigma","sigma.Bs","sigma.Bq",'sd.res','sd.site','sd.quad') burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) rnorm(1)
[1] 0.6914628
jags.effects.m.time1 <- system.time( data.nest1.r2jags.m <- jags(data=data.nest.list, inits=NULL, parameters.to.save=params, model.file=textConnection(modelString), n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 14993 Initializing model
jags.effects.m.time1
user system elapsed 181.676 0.116 185.379
print(data.nest1.r2jags.m)
Inference for Bugs model at "5", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 38.510 2.574 33.407 36.796 38.491 40.252 43.465 1.002 1800
alpha[2] 26.297 3.525 19.386 23.975 26.278 28.601 33.089 1.001 3000
alpha[3] 45.420 3.574 38.410 43.052 45.369 47.751 52.608 1.001 3000
sd.quad 7.350 0.920 5.374 6.779 7.408 7.969 9.051 1.001 3000
sd.res 7.801 0.490 6.976 7.457 7.755 8.105 8.917 1.001 3000
sd.site 3.074 1.167 1.081 2.217 3.001 3.800 5.604 1.005 440
sigma 7.844 0.679 6.654 7.358 7.796 8.284 9.298 1.001 3000
sigma.Bq 7.401 1.109 5.271 6.652 7.382 8.099 9.631 1.001 3000
sigma.Bs 3.446 1.421 1.136 2.442 3.291 4.290 6.681 1.005 410
deviance 1042.405 18.712 1009.056 1029.219 1041.121 1054.547 1083.272 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 175.1 and DIC = 1217.5
DIC is an estimate of expected predictive error (lower deviance is better).
data.nest1.mcmc.list.m <- as.mcmc(data.nest1.r2jags.m)
STAN
Full effects parameterization
rstanString=" data{ int n; int nSite; int nQuad; vector [n] y; int A2[n]; int A3[n]; int Site[n]; int Quad[n]; } parameters{ real alpha0; real alpha2; real alpha3; real<lower=0> sigma; vector [nSite] beta_Site; real<lower=0> sigma_Site; vector [nQuad] beta_Quad; real<lower=0> sigma_Quad; } model{ real mu[n]; // Priors alpha0 ~ normal( 0 , 100 ); alpha2 ~ normal( 0 , 100 ); alpha3 ~ normal( 0 , 100 ); beta_Site~ normal( 0 , sigma_Site ); sigma_Site ~ cauchy( 0 , 25 ); beta_Quad~ normal( 0 , sigma_Quad ); sigma_Quad ~ cauchy( 0 , 25 ); sigma ~ cauchy( 0 , 25 ); for ( i in 1:n ) { mu[i] <- alpha0 + alpha2*A2[i] + alpha3*A3[i] + beta_Site[Site[i]] + beta_Quad[Quad[i]]; } y ~ normal( mu , sigma ); } "
A2 <- ifelse(data.nest1$A=='a2',1,0) A3 <- ifelse(data.nest1$A=='a3',1,0) data.nest.list <- with(data.nest1, list(y=y, A2=A2, A3=A3, Site=as.numeric(Sites), n=nrow(data.nest1), nSite=length(levels(Sites)), nQuad=length(levels(Quads)), Quad=as.numeric(Quads))) burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps + ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.f.time <- system.time( data.nest1.rstan.f <- stan(data=data.nest.list, model_code=rstanString, pars=c('alpha0','alpha2','alpha3','sigma','sigma_Site', 'sigma_Quad'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.76 seconds (Warm-up) # 5.5 seconds (Sampling) # 7.26 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.69 seconds (Warm-up) # 3.8 seconds (Sampling) # 5.49 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 1.83 seconds (Warm-up) # 5.73 seconds (Sampling) # 7.56 seconds (Total)
print(data.nest1.rstan.f)
Inference for Stan model: rstanString.
3 chains, each with iter=13000; warmup=3000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha0 38.52 0.04 2.28 33.99 37.00 38.57 39.91 43.09 2795 1.00
alpha2 26.38 0.06 3.25 19.80 24.36 26.48 28.39 32.63 2783 1.00
alpha3 45.40 0.06 3.22 38.94 43.44 45.44 47.41 51.60 2829 1.00
sigma 7.84 0.02 0.66 6.70 7.37 7.82 8.25 9.24 1609 1.00
sigma_Site 2.39 0.08 1.61 0.20 1.12 2.14 3.32 6.13 447 1.00
sigma_Quad 7.64 0.02 1.12 5.45 6.85 7.64 8.38 9.85 2098 1.00
lp__ -583.54 1.13 13.65 -607.82 -593.03 -584.72 -575.55 -550.38 145 1.01
Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:12:28 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest1.rstan.f.df <-as.data.frame(extract(data.nest1.rstan.f)) head(data.nest1.rstan.f.df)
alpha0 alpha2 alpha3 sigma sigma_Site sigma_Quad lp__ 1 37.75 27.12 46.91 7.732 0.7185 7.604 -563.0 2 38.05 25.86 48.26 7.777 2.4772 7.498 -585.3 3 36.21 29.77 45.46 8.557 2.1948 7.077 -590.4 4 37.73 33.21 49.94 8.704 6.7076 5.562 -601.9 5 36.58 29.90 47.96 7.692 0.9029 10.274 -582.6 6 38.30 29.33 47.19 8.029 3.3813 6.247 -593.5
data.nest1.mcmc.f<-rstan:::as.mcmc.list.stanfit(data.nest1.rstan.f) plyr:::adply(as.matrix(data.nest1.rstan.f.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 alpha0 38.575 28.2309 36.998 38.575 39.907 48.41 34.2376 43.251 36.4326 40.775 2 alpha2 26.482 13.6165 24.359 26.482 28.386 41.29 20.3399 33.092 23.0974 29.233 3 alpha3 45.438 31.8434 43.437 45.438 47.410 57.45 39.3895 51.914 42.5987 48.755 4 sigma 7.819 6.0881 7.373 7.819 8.247 10.59 6.6687 9.198 7.1035 8.334 5 sigma_Site 2.143 0.1809 1.118 2.143 3.325 12.33 0.1809 5.371 0.1809 2.963 6 sigma_Quad 7.639 3.3836 6.846 7.639 8.382 12.26 5.4516 9.851 6.6402 8.768 7 lp__ -584.722 -623.1653 -593.031 -584.722 -575.551 -540.56 -604.7332 -549.884 -598.8459 -573.657
Matrix parameterization
rstanString=" data{ int n; int nSite; int nQuad; int nA; vector [n] y; matrix [n,nA] X; int Site[n]; int Quad[n]; vector [nA] a0; matrix [nA,nA] A0; } parameters{ vector [nA] alpha; real<lower=0> sigma; vector [nSite] beta_Site; real<lower=0> sigma_Site; vector [nQuad] beta_Quad; real<lower=0> sigma_Quad; } model{ real mu[n]; // Priors //alpha ~ normal( 0 , 100 ); alpha ~ multi_normal(a0,A0); beta_Site ~ normal( 0 , sigma_Site ); sigma_Site ~ cauchy( 0 , 25); beta_Quad ~ normal( 0 , sigma_Quad ); sigma_Quad ~ cauchy( 0 , 25); sigma ~ cauchy( 0 , 25 ); for ( i in 1:n ) { mu[i] <- dot_product(X[i],alpha) + beta_Site[Site[i]] + beta_Quad[Quad[i]]; } y ~ normal( mu , sigma ); } "
X <- model.matrix(~A, data.nest) nA <- ncol(X) data.nest.list <- with(data.nest1, list(y=y, X=X, Site=as.numeric(Sites), Quad=as.numeric(Quads), n=nrow(data.nest1), nSite=length(levels(Sites)), nQuad=length(levels(Quads)), nA=nA, a0=rep(0,nA), A0=diag(100000,nA))) burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) rstan.m.time <- system.time( data.nest1.rstan.m <- stan(data=data.nest.list, model_code=rstanString, pars=c('alpha','sigma','sigma_Site', 'sigma_Quad'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE ) )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 3.19 seconds (Warm-up) # 9.42 seconds (Sampling) # 12.61 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 3.59 seconds (Warm-up) # 10.41 seconds (Sampling) # 14 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 3.97 seconds (Warm-up) # 28.8 seconds (Sampling) # 32.77 seconds (Total)
print(data.nest1.rstan.m)
Inference for Stan model: rstanString.
3 chains, each with iter=13000; warmup=3000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha[1] 38.53 0.04 2.30 33.94 37.00 38.52 40.01 42.98 2643 1
alpha[2] 26.27 0.06 3.26 19.84 24.10 26.23 28.33 32.59 3000 1
alpha[3] 45.41 0.06 3.25 38.98 43.26 45.49 47.46 51.61 3000 1
sigma 7.87 0.01 0.67 6.70 7.41 7.82 8.27 9.35 2749 1
sigma_Site 2.48 0.05 1.58 0.30 1.25 2.26 3.42 6.15 1177 1
sigma_Quad 7.64 0.02 1.14 5.51 6.89 7.63 8.40 9.86 2340 1
lp__ -584.35 0.41 13.01 -607.32 -593.42 -585.09 -576.81 -555.47 1005 1
Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:20:14 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
data.nest1.rstan.m.df <-as.data.frame(extract(data.nest1.rstan.m)) head(data.nest1.rstan.m.df)
alpha.1 alpha.2 alpha.3 sigma sigma_Site sigma_Quad lp__ 1 32.75 31.91 50.51 7.634 3.0127 7.464 -594.2 2 39.40 23.76 42.90 6.620 2.3567 8.884 -572.7 3 38.35 24.41 43.42 7.147 0.7239 9.753 -570.9 4 39.64 26.10 44.11 7.187 2.1584 8.311 -572.4 5 38.01 27.74 42.38 6.840 2.1693 9.145 -583.1 6 37.63 26.06 46.30 7.771 0.6094 8.379 -571.7
data.nest1.mcmc.m<-rstan:::as.mcmc.list.stanfit(data.nest1.rstan.m) plyr:::adply(as.matrix(data.nest1.rstan.m.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 alpha.1 38.525 30.21146 37.001 38.525 40.005 48.21 34.14305 43.134 36.2077 40.704 2 alpha.2 26.226 14.60060 24.104 26.226 28.333 39.52 20.32018 33.020 23.0563 29.346 3 alpha.3 45.488 32.75320 43.264 45.488 47.456 61.27 39.20062 51.789 42.4782 48.693 4 sigma 7.824 5.87588 7.407 7.824 8.272 10.88 6.58580 9.169 7.0994 8.378 5 sigma_Site 2.258 0.07567 1.246 2.258 3.425 13.30 0.07567 5.307 0.2434 3.118 6 sigma_Quad 7.626 1.84726 6.888 7.626 8.404 12.30 5.48287 9.823 6.6016 8.799 7 lp__ -585.088 -624.80265 -593.424 -585.088 -576.809 -527.77 -609.25382 -557.749 -599.5603 -575.088
$R^2$ and finite population standard deviations
If we use the JAGS matrix parameterization model from above, the JAGS model is already complete (as we defined the sd components in that model already).
data.nest1.mcmc.listSD <- as.mcmc(data.nest1.r2jags.m) Xmat <- model.matrix(~A, data.nest1) coefs <- data.nest.r2jags.m$BUGSoutput$sims.list[['alpha']] fitted <- coefs %*% t(Xmat) X.var <- aaply(fitted,1,function(x){var(x)}) Z.var <- data.nest.r2jagsSD$BUGSoutput$sims.list[['sd.site']]^2 R.var <- data.nest.r2jagsSD$BUGSoutput$sims.list[['sd.y']]^2 R2.marginal <- (X.var)/(X.var+Z.var+R.var) R2.marginal <- data.frame(Mean=mean(R2.marginal), Median=median(R2.marginal), HPDinterval(as.mcmc(R2.marginal))) R2.conditional <- (X.var+Z.var)/(X.var+Z.var+R.var) R2.conditional <- data.frame(Mean=mean(R2.conditional), Median=median(R2.conditional), HPDinterval(as.mcmc(R2.conditional))) R2.site <- (Z.var)/(X.var+Z.var+R.var) R2.site <- data.frame(Mean=mean(R2.site), Median=median(R2.site), HPDinterval(as.mcmc(R2.site))) R2.res<-(R.var)/(X.var+Z.var+R.var) R2.res <- data.frame(Mean=mean(R2.res), Median=median(R2.res), HPDinterval(as.mcmc(R2.res))) rbind(R2.site=R2.site, R2.marginal=R2.marginal, R2.res=R2.res, R2.conditional=R2.conditional)
Mean Median lower upper R2.site 0.40326358 0.39162062 0.21710229 0.62151297 R2.marginal 0.55526156 0.56689160 0.32820803 0.76703797 R2.res 0.04147485 0.04007836 0.02189078 0.06277313 R2.conditional 0.95852515 0.95992164 0.93722687 0.97810922
BRMS (STAN)
library(brms) data.nest1$fQuads <- interaction(data.nest1$Sites, data.nest1$Quads) data.nest1.brm <- brm(y~A+(1|Sites) + (1|Quads), data=data.nest1, family='gaussian', prior=c(set_prior('normal(0,100)', class='b'), set_prior('cauchy(0,5)', class='sd')), n.chains=3, n.iter=2000, warmup=500, n.thin=2 )
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Chain 1, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 1, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 1, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 1, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 1, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 1, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 1, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 1, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 1, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 1, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 1, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 1, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 1.08899 seconds (Warm-up) # 1.704 seconds (Sampling) # 2.793 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Chain 2, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 2, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 2, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 2, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 2, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 2, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 2, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 2, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 2, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 2, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 2, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 2, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 0.634045 seconds (Warm-up) # 1.19444 seconds (Sampling) # 1.82849 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Chain 3, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 3, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 3, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 3, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 3, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 3, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 3, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 3, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 3, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 3, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 3, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 3, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 0.6651 seconds (Warm-up) # 0.884811 seconds (Sampling) # 1.54991 seconds (Total)
summary(data.nest1.brm)
Family: gaussian (identity)
Formula: y ~ A + (1 | Sites) + (1 | Quads)
Data: data.nest1 (Number of observations: 150)
Samples: 3 chains, each with n.iter = 2000; n.warmup = 500; n.thin = 2;
total post-warmup samples = 2250
WAIC: 1096.55
Random Effects:
~Quads (Number of levels: 75)
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sd(Intercept) 7.5 1.09 5.31 9.69 973 1
~Sites (Number of levels: 15)
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sd(Intercept) 2.02 1.4 0.09 5.21 675 1
Fixed Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept 38.49 2.21 34.17 42.76 1143 1
Aa2 26.19 3.09 20.28 32.27 1207 1
Aa3 45.47 3.10 39.51 51.49 1395 1
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sigma(y) 7.87 0.68 6.67 9.32 778 1
Samples were drawn using NUTS(diag_e). For each parameter, Eff.Sample is a
crude measure of effective sample size, and Rhat is the potential scale
reduction factor on split chains (at convergence, Rhat = 1).
brms:::stancode(data.nest1.brm)
functions {
}
data {
int<lower=1> N; # number of observations
vector[N] Y; # response variable
int<lower=1> K; # number of fixed effects
matrix[N, K] X; # FE design matrix
# data for random effects of Quads
int<lower=1> J_1[N]; # RE levels
int<lower=1> N_1; # number of levels
int<lower=1> K_1; # number of REs
real Z_1[N]; # RE design matrix
# data for random effects of Sites
int<lower=1> J_2[N]; # RE levels
int<lower=1> N_2; # number of levels
int<lower=1> K_2; # number of REs
real Z_2[N]; # RE design matrix
}
transformed data {
}
parameters {
real b_Intercept; # fixed effects Intercept
vector[K] b; # fixed effects
vector[N_1] pre_1; # unscaled REs
real<lower=0> sd_1; # RE standard deviation
vector[N_2] pre_2; # unscaled REs
real<lower=0> sd_2; # RE standard deviation
real<lower=0> sigma; # residual SD
}
transformed parameters {
vector[N] eta; # linear predictor
vector[N_1] r_1; # REs
vector[N_2] r_2; # REs
# compute linear predictor
eta <- X * b + b_Intercept;
r_1 <- sd_1 * (pre_1); # scale REs
r_2 <- sd_2 * (pre_2); # scale REs
# if available add REs to linear predictor
for (n in 1:N) {
eta[n] <- eta[n] + Z_1[n] * r_1[J_1[n]] + Z_2[n] * r_2[J_2[n]];
}
}
model {
# prior specifications
b_Intercept ~ normal(0,100);
b ~ normal(0,100);
sd_1 ~ cauchy(0,5);
pre_1 ~ normal(0, 1);
sd_2 ~ cauchy(0,5);
pre_2 ~ normal(0, 1);
sigma ~ cauchy(0, 22);
# likelihood contribution
Y ~ normal(eta, sigma);
}
generated quantities {
}
#brms:::standata(data.nest1.brm)
Worked Examples
Nested ANOVA (Mixed effects) references
- McCarthy (2007) - Chpt ?
- Kery (2010) - Chpt ?
- Gelman & Hill (2007) - Chpt ?
- Logan (2010) - Chpt 12
- Quinn & Keough (2002) - Chpt 9
Nested ANOVA - one between factor
In an unusually detailed preparation for an Environmental Effects Statement for a proposed discharge of dairy wastes into the Curdies River, in western Victoria, a team of stream ecologists wanted to describe the basic patterns of variation in a stream invertebrate thought to be sensitive to nutrient enrichment. As an indicator species, they focused on a small flatworm, Dugesia, and started by sampling populations of this worm at a range of scales. They sampled in two seasons, representing different flow regimes of the river - Winter and Summer. Within each season, they sampled three randomly chosen (well, haphazardly, because sites are nearly always chosen to be close to road access) sites. A total of six sites in all were visited, 3 in each season. At each site, they sampled six stones, and counted the number of flatworms on each stone.
Download Curdies data set| Format of curdies.csv data files | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||||||||||||||||||||||||||||
The hierarchical nature of this design can be appreciated when we examine an illustration of the spatial and temporal scale of the measurements.
- Within each of the two Seasons, there were three separate Sites (Sites not repeatidly measured across Seasons).
- Within each of the Sites, six logs were selected (haphazardly) from which the number of flatworms were counted.
We construct the model in much the same way. That is:
- The observed number of flatworm per log (for a given Site) is equal to (modelled against) the mean number for that Site
plus a random amount drawn from a normal distribution with a mean of zero and a certain degree of variability (precision).
Number of flatwormlog i = βSite j,i + εi where ε ∼ N(0,σ2)
- The mean number of flatworm per Site (within a given Season) is equal to (modelled against) the mean number for that Season
plus a random amount drawn from a normal distribution with a means of zero and a certain degree of variability (precision).
μSite j = γSeason j + εj where ε ∼ N(0,σ2)
The SITE variable is conveniently already coded as a numeric series (starting at 1).
Open the curdies data file.curdies <- read.table('../downloads/data/curdies.csv', header=T, sep=',', strip.white=T) head(curdies)
SEASON SITE DUGESIA S4DUGES 1 WINTER 1 0.6476829 0.8970995 2 WINTER 1 6.0961516 1.5713175 3 WINTER 1 1.3105639 1.0699526 4 WINTER 1 1.7252788 1.1460797 5 WINTER 1 1.4593867 1.0991136 6 WINTER 1 1.0575610 1.0140897
- Lets start by performing some exploratory data analysis to help us identify any issues with the data as
well as helping to try to identify a possible model to fit.
- Boxplots for the main effect (Season)
Show codeIs there any evidence of non-normality and/or heterogeneity (Y or N)
library(dplyr) curdies.ag <- curdies %>% group_by(SEASON,SITE) %>% summarize(DUGESIA=mean(DUGESIA)) curdies.ag
Source: local data frame [6 x 3] Groups: SEASON SEASON SITE DUGESIA 1 SUMMER 4 0.4190947 2 SUMMER 5 0.2290862 3 SUMMER 6 0.1942443 4 WINTER 1 2.0494375 5 WINTER 2 4.1819078 6 WINTER 3 0.6782063
#OR equivalently with the plyr package library(plyr) ddply(curdies, ~SEASON+SITE, numcolwise(mean))
SEASON SITE DUGESIA S4DUGES 1 SUMMER 4 0.4190947 0.3508213 2 SUMMER 5 0.2290862 0.1804622 3 SUMMER 6 0.1942443 0.3811223 4 WINTER 1 2.0494375 1.1329421 5 WINTER 2 4.1819078 1.2718698 6 WINTER 3 0.6782063 0.8678707
detach(package:plyr) #since dplyr and plyr do not play nicely together library(ggplot2) ggplot(curdies.ag, aes(y=DUGESIA, x=SEASON)) + geom_boxplot()
If so, assess whether a transformation (such as a forth-root transformation) will address the violations and then make the appropriate corrections - Consider a transformation (such as forth-root transform) and redo boxplots for the main effect (Season)
Show codeDoes a forth-root transformation improve the data with respect to normality and homogeneity of variance (Y or N)?
curdies.ag <- curdies %>% group_by(SEASON,SITE) %>% summarize(DUGESIA=mean(DUGESIA^0.25)) curdies.ag
Source: local data frame [6 x 3] Groups: SEASON SEASON SITE DUGESIA 1 SUMMER 4 0.3508213 2 SUMMER 5 0.1804622 3 SUMMER 6 0.3811223 4 WINTER 1 1.1329421 5 WINTER 2 1.2718698 6 WINTER 3 0.8678707
ggplot(curdies.ag, aes(y=DUGESIA, x=SEASON)) + geom_boxplot()
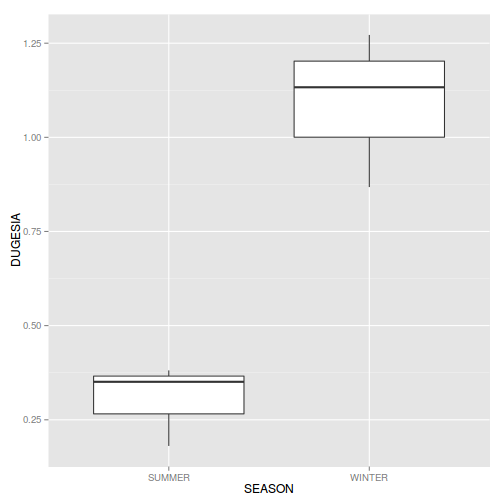
- Boxplots for the main effect (Season)
- Fit the hierarchical model.
Use with effects (or matrix) parameterization for the 'fixed effects' and means (or matrix) parameterization for the 'random effects'.
Note the following points:
- Non-informative priors for residual precision (standard deviations) should be defined as vague uniform distributions rather than gamma distributions. This prevents the chains from walking to close to parameter estimates of 0. Alternatively, Gelman recommends the use of weakly informative half-cauchy distributions for variances in hierarchical designs.
- Finite-population standard deviation for Site (the within group factor) should reflect standard deviation between Sites within season (not standard deviation between all Sites). Unfortunately, the BUGS language does not offer a mechanism to determine which indexes match certain criteria (for example which Sites correspond to which Season), nor does it allow variables to be redefined. One way to allow us to generate multiple standard deviations is to create an offset vector that can be used to indicate the range of Site numbers that are within which Season.
- As this is a multi-level design in which the Season 'replicates' are determined by the Site means, it is important that firstly, the number of levels of the within Group factor (Season) reflects this, and secondly that the factor levels of the within group factor (Season) correspond to the factor levels of the group factor (Site). In this case, the Sites are labeled 1-6, but the first three Sites are in Winter. R will naturally label Winter as the second level (as alphabetically W comes after S for summer). Thus without intervention or careful awareness, it will appear that the Winter means are higher than the Summer means, when it is actually the other way around. One way to check this, is create the data list and check that all the factor levels are listed in increasing numerical order.
View preparation codesites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 4 1 7
curdies.list <- with(curdies, list(dugesia=DUGESIA, season=as.numeric(SEASON), site=as.numeric(SITE), n=nrow(curdies), nSeason=length(levels(as.factor(SEASON))), nSite=length(levels(as.factor(SITE))), SiteOffset=offset ) ) curdies.list
$dugesia [1] 0.6477 6.0962 1.3106 1.7253 1.4594 1.0576 1.0163 16.1968 1.1681 1.0243 2.0113 3.6746 [13] 0.6891 1.2191 1.1131 0.6569 0.1361 0.2547 0.0000 0.0000 0.9411 0.0000 0.0000 1.5735 [25] 1.3745 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1329 0.0000 0.6580 0.3745 $season [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 $site [1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6 $n [1] 36 $nSeason [1] 2 $nSite [1] 6 $SiteOffset [1] 4 1 7
## notice that The Season variable has as many entries as there were plots ## rather than having as many as there were Sites. ## Also notice that Winter is the second Season according to the factor levels ## Finally notice that the offset values are not in order #season <- with(curdies,SEASON[match(unique(SITE),SITE)]) #season <- factor(season, levels=unique(season)) curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 1 4 7
curdies.list <- with(curdies, list(dugesia=DUGESIA, season=as.numeric(SEASON), site=as.numeric(SITE), n=nrow(curdies), nSeason=length(levels(SEASON)), nSite=length(levels(as.factor(SITE))), SiteOffset=offset ) ) curdies.list
$dugesia [1] 0.6477 6.0962 1.3106 1.7253 1.4594 1.0576 1.0163 16.1968 1.1681 1.0243 2.0113 3.6746 [13] 0.6891 1.2191 1.1131 0.6569 0.1361 0.2547 0.0000 0.0000 0.9411 0.0000 0.0000 1.5735 [25] 1.3745 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1329 0.0000 0.6580 0.3745 $season [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 $site [1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6 $n [1] 36 $nSeason [1] 2 $nSite [1] 6 $SiteOffset [1] 1 4 7
## That is betterShow full effects parameterization JAGS codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha0 + alpha[SEASON[i]] + beta[SITE[i]] y.err[i] <- y[i] - mu[i] } #Priors alpha0 ~ dnorm(0, 1.0E-6) alpha[1] <- 0 for (i in 2:nSEASON) { alpha[i] ~ dnorm(0, 1.0E-6) #prior } for (i in 1:nSITE) { beta[i] ~ dnorm(0, tau.B) #prior } #Uniform uninformative prior on variance tau <- 1 / (sigma * sigma) tau.B <- 1 / (sigma.B * sigma.B) sigma ~ dunif(0, 100) sigma.B ~ dunif(0, 100) for (i in 1:nSEASON) { SD.Site[i] <- sd(beta[SiteOffset[i]:SiteOffset[i+1]-1]) } sd.Season <- sd(alpha) sd.Site <- mean(SD.Site) #sd(beta.site) sd.Resid <- sd(y.err) } " writeLines(modelString,con="../downloads/BUGSscripts/ws9.2bS1.2a.txt") # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 1 4 7
curdies$SITE <- factor(curdies$SITE) curdies.list <- with(curdies, list(y=S4DUGES, SITE=as.numeric(SITE), SEASON=as.numeric(SEASON), n=nrow(curdies), nSITE=length(levels(SITE)), nSEASON = length(levels(SEASON)), SiteOffset=offset ) ) curdies.list
$y [1] 0.8971 1.5713 1.0700 1.1461 1.0991 1.0141 1.0040 2.0061 1.0396 1.0060 1.1909 1.3845 0.9111 1.0508 1.0272 0.9003 0.6074 0.7104 0.0000 0.0000 0.9849 0.0000 0.0000 1.1200 1.0828 0.0000 0.0000 0.0000 [29] 0.0000 0.0000 0.0000 0.0000 0.6038 0.0000 0.9007 0.7823 $SITE [1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6 $SEASON [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 $n [1] 36 $nSITE [1] 6 $nSEASON [1] 2 $SiteOffset [1] 1 4 7
# define parameters params <- c("alpha0","alpha","sigma","sigma.B","sd.Season","sd.Site","sd.Resid","SD.Site") burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) curdies.r2jags.a <- jags(data=curdies.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.2bS1.2a.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 176 Initializing model
print(curdies.r2jags.a)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2a.txt", fit using jags, 3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff SD.Site[1] 0.116 0.091 0.003 0.042 0.098 0.172 0.331 1.006 1300 SD.Site[2] 0.095 0.073 0.003 0.038 0.079 0.135 0.273 1.007 770 alpha[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 alpha[2] -0.789 0.239 -1.261 -0.911 -0.788 -0.662 -0.338 1.002 2100 alpha0 1.093 0.169 0.770 1.010 1.090 1.175 1.426 1.001 2300 sd.Resid 0.387 0.015 0.366 0.377 0.386 0.394 0.425 1.002 3000 sd.Season 0.560 0.160 0.247 0.468 0.557 0.645 0.892 1.005 1200 sd.Site 0.105 0.071 0.004 0.048 0.098 0.151 0.269 1.008 870 sigma 0.404 0.055 0.316 0.366 0.399 0.433 0.529 1.001 3000 sigma.B 0.173 0.164 0.005 0.066 0.128 0.229 0.614 1.008 560 deviance 35.022 3.511 29.717 32.605 34.482 36.802 43.431 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 6.2 and DIC = 41.2 DIC is an estimate of expected predictive error (lower deviance is better).curdies.mcmc.a <- as.mcmc(curdies.r2jags.a)
Show matrix parameterization JAGS codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- inprod(alpha[],X[i,]) + beta[SITE[i]] y.err[i] <- y[i] - mu[i] } #Priors alpha ~ dmnorm(a0, A0) for (i in 1:nSITE) { beta[i] ~ dnorm(0, tau.B) #prior } #Uniform uninformative prior on variance tau <- 1 / (sigma * sigma) tau.B <- 1 / (sigma.B * sigma.B) sigma ~ dunif(0, 100) sigma.B ~ dunif(0, 100) # Finite-population standard deviations for (i in 1:nSEASON) { SD.Site[i] <- sd(beta[SiteOffset[i]:SiteOffset[i+1]-1]) } seasons[1] <- alpha[1] for (i in 2:nSEASON) { seasons[i] <- alpha[1]+alpha[i] } sd.Season <- sd(seasons) sd.Site <- mean(SD.Site) sd.Resid <- sd(y.err) } " writeLines(modelString,con="../downloads/BUGSscripts/ws9.2bS1.2b.txt") # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 1 4 7
curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=curdies) curdies.list <- with(curdies, list(y=S4DUGES, SITE=as.numeric(SITE), X=Xmat, n=nrow(curdies), nSITE=length(levels(SITE)), nSEASON=length(levels(SEASON)), a0=rep(0, ncol(Xmat)), A0=diag(0, ncol(Xmat)), SiteOffset=offset ) ) curdies.list
$y [1] 0.8971 1.5713 1.0700 1.1461 1.0991 1.0141 1.0040 2.0061 1.0396 1.0060 1.1909 1.3845 0.9111 1.0508 1.0272 0.9003 0.6074 0.7104 0.0000 0.0000 0.9849 0.0000 0.0000 1.1200 1.0828 0.0000 0.0000 0.0000 [29] 0.0000 0.0000 0.0000 0.0000 0.6038 0.0000 0.9007 0.7823 $SITE [1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6 $X (Intercept) SEASONSUMMER 1 1 0 2 1 0 3 1 0 4 1 0 5 1 0 6 1 0 7 1 0 8 1 0 9 1 0 10 1 0 11 1 0 12 1 0 13 1 0 14 1 0 15 1 0 16 1 0 17 1 0 18 1 0 19 1 1 20 1 1 21 1 1 22 1 1 23 1 1 24 1 1 25 1 1 26 1 1 27 1 1 28 1 1 29 1 1 30 1 1 31 1 1 32 1 1 33 1 1 34 1 1 35 1 1 36 1 1 attr(,"assign") [1] 0 1 attr(,"contrasts") attr(,"contrasts")$SEASON [1] "contr.treatment" $n [1] 36 $nSITE [1] 6 $nSEASON [1] 2 $a0 [1] 0 0 $A0 [,1] [,2] [1,] 0 0 [2,] 0 0 $SiteOffset [1] 1 4 7# define parameters params <- c("alpha","sigma","sigma.B","sd.Season","sd.Site","sd.Resid","SD.Site") burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) curdies.r2jags.b <- jags(data=curdies.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.2bS1.2b.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 258 Initializing model
print(curdies.r2jags.b)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2b.txt", fit using jags, 3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff SD.Site[1] 0.115 0.090 0.004 0.041 0.096 0.171 0.324 1.015 490 SD.Site[2] 0.092 0.071 0.003 0.036 0.077 0.134 0.265 1.023 370 alpha[1] 1.088 0.170 0.756 1.001 1.085 1.176 1.425 1.005 2400 alpha[2] -0.786 0.230 -1.245 -0.907 -0.786 -0.663 -0.327 1.002 3000 sd.Resid 0.388 0.015 0.366 0.378 0.386 0.394 0.424 1.001 3000 sd.Season 0.557 0.158 0.237 0.469 0.556 0.642 0.880 1.001 3000 sd.Site 0.104 0.070 0.004 0.046 0.094 0.151 0.258 1.028 330 sigma 0.403 0.054 0.315 0.366 0.396 0.434 0.522 1.001 3000 sigma.B 0.169 0.157 0.006 0.064 0.132 0.226 0.552 1.022 440 deviance 35.038 3.445 29.819 32.678 34.494 36.737 43.569 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 5.9 and DIC = 41.0 DIC is an estimate of expected predictive error (lower deviance is better).curdies.mcmc.b <- as.mcmc(curdies.r2jags.b)
Hierarchical parameterization JAGS codemodelString=" model { #Likelihood #Likelihood (esimating site means (gamma.site) for (i in 1:n) { y[i]~dnorm(quad.means[i],tau) quad.means[i] <- gamma.site[SITE[i]] y.err[i] <- y[i] - quad.means[i] } for (i in 1:nSITE) { gamma.site[i] ~ dnorm(site.means[i], tau.site) site.means[i] <- inprod(beta[],X[i,]) } #Priors for (i in 1:nX) { beta[i] ~ dnorm(0, 1.0E-6) #prior } sigma ~ dunif(0, 100) tau <- 1 / (sigma * sigma) sigma.site ~ dunif(0, 100) tau.site <- 1 / (sigma.site * sigma.site) # Finite-population standard deviations for (i in 1:nSEASON) { SD.Site[i] <- sd(gamma.site[SiteOffset[i]:SiteOffset[i+1]-1]) } seasons[1] <- beta[1] for (i in 2:nSEASON) { seasons[i] <- beta[1]+beta[i] } sd.Season <- sd(seasons) sd.Site <- mean(SD.Site) sd.Resid <- sd(y.err) } " writeLines(modelString,con="../downloads/BUGSscripts/ws9.2bS1.2c.txt") # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 1 4 7
curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=ddply(curdies, ~SITE, catcolwise(unique))) curdies.list <- with(curdies, list(y=S4DUGES, SITE=as.numeric(SITE), X=Xmat, nX=ncol(Xmat), n=nrow(curdies), nSITE=length(levels(SITE)), nSEASON=length(levels(SEASON)), SiteOffset=offset ) ) curdies.list
$y [1] 0.8971 1.5713 1.0700 1.1461 1.0991 1.0141 1.0040 2.0061 1.0396 1.0060 1.1909 1.3845 0.9111 1.0508 1.0272 0.9003 0.6074 0.7104 0.0000 0.0000 0.9849 0.0000 0.0000 1.1200 1.0828 0.0000 0.0000 0.0000 [29] 0.0000 0.0000 0.0000 0.0000 0.6038 0.0000 0.9007 0.7823 $SITE [1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6 $X (Intercept) SEASONSUMMER 1 1 0 2 1 0 3 1 0 4 1 1 5 1 1 6 1 1 attr(,"assign") [1] 0 1 attr(,"contrasts") attr(,"contrasts")$SEASON [1] "contr.treatment" $nX [1] 2 $n [1] 36 $nSITE [1] 6 $nSEASON [1] 2 $SiteOffset [1] 1 4 7
# define parameters params <- c("beta","sigma","sigma.site","sd.Season","sd.Site","sd.Resid") burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) curdies.r2jags.c <- jags(data=curdies.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.2bS1.2c.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 156 Initializing model
print(curdies.r2jags.c)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2c.txt", fit using jags, 3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff beta[1] 1.089 0.172 0.757 1.001 1.086 1.178 1.414 1.001 3000 beta[2] -0.783 0.241 -1.255 -0.905 -0.780 -0.662 -0.350 1.001 3000 sd.Resid 0.388 0.015 0.366 0.377 0.386 0.394 0.423 1.002 1800 sd.Season 0.556 0.162 0.254 0.468 0.552 0.640 0.887 1.006 3000 sd.Site 0.104 0.071 0.003 0.047 0.094 0.150 0.261 1.003 970 sigma 0.402 0.053 0.314 0.365 0.396 0.433 0.515 1.002 1400 sigma.site 0.179 0.187 0.004 0.061 0.134 0.235 0.654 1.002 1100 deviance 34.970 3.365 29.820 32.577 34.405 36.866 42.802 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 5.7 and DIC = 40.6 DIC is an estimate of expected predictive error (lower deviance is better).curdies.mcmc.c <- as.mcmc(curdies.r2jags.c)
Matrix parameterization STAN codeUnfortunately, STAN does not yet support vector indexing or the ability to multiply a matrix by a vector. A work around involves multiplication of a dummy matrix with the gamma vector..rstanString= # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 1 4 7
curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=curdies) Zmat <- model.matrix(~-1+SITE, data=curdies) curdies.list <- with(curdies, list(y=S4DUGES, Z=Zmat, X=Xmat, nX=ncol(Xmat), nZ=ncol(Zmat), n=nrow(curdies), a0=rep(0,ncol(Xmat)), A0=diag(100000,ncol(Xmat)), SiteOffset=offset, m=matrix(rep(1,6),2) ) ) curdies.list
$y [1] 0.8971 1.5713 1.0700 1.1461 1.0991 1.0141 1.0040 2.0061 1.0396 1.0060 1.1909 1.3845 0.9111 1.0508 1.0272 0.9003 0.6074 0.7104 0.0000 0.0000 0.9849 0.0000 0.0000 1.1200 1.0828 0.0000 0.0000 0.0000 [29] 0.0000 0.0000 0.0000 0.0000 0.6038 0.0000 0.9007 0.7823 $Z SITE1 SITE2 SITE3 SITE4 SITE5 SITE6 1 1 0 0 0 0 0 2 1 0 0 0 0 0 3 1 0 0 0 0 0 4 1 0 0 0 0 0 5 1 0 0 0 0 0 6 1 0 0 0 0 0 7 0 1 0 0 0 0 8 0 1 0 0 0 0 9 0 1 0 0 0 0 10 0 1 0 0 0 0 11 0 1 0 0 0 0 12 0 1 0 0 0 0 13 0 0 1 0 0 0 14 0 0 1 0 0 0 15 0 0 1 0 0 0 16 0 0 1 0 0 0 17 0 0 1 0 0 0 18 0 0 1 0 0 0 19 0 0 0 1 0 0 20 0 0 0 1 0 0 21 0 0 0 1 0 0 22 0 0 0 1 0 0 23 0 0 0 1 0 0 24 0 0 0 1 0 0 25 0 0 0 0 1 0 26 0 0 0 0 1 0 27 0 0 0 0 1 0 28 0 0 0 0 1 0 29 0 0 0 0 1 0 30 0 0 0 0 1 0 31 0 0 0 0 0 1 32 0 0 0 0 0 1 33 0 0 0 0 0 1 34 0 0 0 0 0 1 35 0 0 0 0 0 1 36 0 0 0 0 0 1 attr(,"assign") [1] 1 1 1 1 1 1 attr(,"contrasts") attr(,"contrasts")$SITE [1] "contr.treatment" $X (Intercept) SEASONSUMMER 1 1 0 2 1 0 3 1 0 4 1 0 5 1 0 6 1 0 7 1 0 8 1 0 9 1 0 10 1 0 11 1 0 12 1 0 13 1 0 14 1 0 15 1 0 16 1 0 17 1 0 18 1 0 19 1 1 20 1 1 21 1 1 22 1 1 23 1 1 24 1 1 25 1 1 26 1 1 27 1 1 28 1 1 29 1 1 30 1 1 31 1 1 32 1 1 33 1 1 34 1 1 35 1 1 36 1 1 attr(,"assign") [1] 0 1 attr(,"contrasts") attr(,"contrasts")$SEASON [1] "contr.treatment" $nX [1] 2 $nZ [1] 6 $n [1] 36 $a0 [1] 0 0 $A0 [,1] [,2] [1,] 1e+05 0e+00 [2,] 0e+00 1e+05 $SiteOffset [1] 1 4 7 $m [,1] [,2] [,3] [1,] 1 1 1 [2,] 1 1 1# define parameters burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) curdies.rstan.a <- stan(data=curdies.list, model_code=rstanString, pars=c('beta','gamma','sigma','sigma_Z','sd_Resid','sd_Season','sd_Site'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.42 seconds (Warm-up) # 1.39 seconds (Sampling) # 1.81 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.45 seconds (Warm-up) # 1.56 seconds (Sampling) # 2.01 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.41 seconds (Warm-up) # 1.42 seconds (Sampling) # 1.83 seconds (Total)
print(curdies.rstan.a)
Inference for Stan model: rstanString. 3 chains, each with iter=13000; warmup=3000; thin=10; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 1.09 0.00 0.18 0.72 0.99 1.09 1.18 1.42 3000 1 beta[2] -0.78 0.01 0.24 -1.22 -0.91 -0.78 -0.65 -0.30 2248 1 gamma[1] 0.03 0.00 0.17 -0.30 -0.05 0.01 0.09 0.42 3000 1 gamma[2] 0.08 0.00 0.18 -0.22 -0.01 0.04 0.15 0.51 2431 1 gamma[3] -0.09 0.00 0.19 -0.53 -0.17 -0.06 0.00 0.19 2813 1 gamma[4] 0.02 0.00 0.17 -0.33 -0.05 0.01 0.09 0.36 3000 1 gamma[5] -0.06 0.00 0.17 -0.46 -0.12 -0.03 0.02 0.23 2882 1 gamma[6] 0.03 0.00 0.17 -0.29 -0.04 0.02 0.10 0.40 2857 1 sigma 0.40 0.00 0.05 0.32 0.37 0.40 0.44 0.53 1447 1 sigma_Z 0.19 0.00 0.18 0.02 0.07 0.14 0.24 0.62 1463 1 sd_Resid 0.39 0.00 0.02 0.37 0.38 0.39 0.39 0.42 2299 1 sd_Season 0.55 0.00 0.16 0.22 0.46 0.55 0.64 0.87 2129 1 sd_Site 0.11 0.00 0.07 0.01 0.06 0.10 0.16 0.26 874 1 lp__ 22.43 0.20 4.50 13.77 19.47 22.24 25.20 31.53 518 1 Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:28:34 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).curdies.mcmc.d <- rstan:::as.mcmc.list.stanfit(curdies.rstan.a) curdies.mcmc.df.d <- as.data.frame(extract(curdies.rstan.a)) SD.site <- NULL sd.site <- curdies.mcmc.df.d[,3:8] for (i in 1:length(levels(curdies$SEASON))) { SD.site <- c(SD.site,apply(sd.site[,offset[i]:(offset[i+1]-1)],1,sd)) } data.frame(mean=mean(SD.site), median=median(SD.site), HPDinterval(as.mcmc(SD.site)), HPDinterval(as.mcmc(SD.site),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.1115 0.09236 0.003046 0.2739 0.003046 0.1377
Hierarchical parameterization STAN coderstanString=" data{ int n; int nZ; int nX; vector [n] y; matrix [nZ,nX] X; matrix [n,nZ] Z; } parameters{ vector [nX] beta; real<lower=0> sigma; vector [nZ] gamma; real<lower=0> sigma_Z; } transformed parameters { vector [n] mu_Z; vector [nZ] mu; mu_Z <- Z*gamma; mu <- X*beta; } model{ // Priors beta ~ normal(0, 10000); gamma ~ normal( 0 , 1000); sigma_Z ~ uniform( 0 , 100 ); sigma ~ uniform( 0 , 100 ); y ~ normal(mu_Z, sigma); gamma ~ normal( mu , sigma_Z ); } generated quantities { vector [n] y_err; real<lower=0> sd_Resid; y_err <- y - mu_Z; sd_Resid <- sd(y_err); } " # Generate a data list curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=ddply(curdies, ~SITE, catcolwise(unique))) Zmat <- model.matrix(~-1+SITE, data=curdies) curdies.list <- with(curdies, list(y=S4DUGES, Z=Zmat, X=Xmat, nX=ncol(Xmat), nZ=ncol(Zmat), n=nrow(curdies) ) ) curdies.list
$y [1] 0.8971 1.5713 1.0700 1.1461 1.0991 1.0141 1.0040 2.0061 1.0396 1.0060 1.1909 1.3845 0.9111 1.0508 1.0272 0.9003 0.6074 0.7104 0.0000 0.0000 0.9849 0.0000 0.0000 1.1200 1.0828 0.0000 0.0000 0.0000 [29] 0.0000 0.0000 0.0000 0.0000 0.6038 0.0000 0.9007 0.7823 $Z SITE1 SITE2 SITE3 SITE4 SITE5 SITE6 1 1 0 0 0 0 0 2 1 0 0 0 0 0 3 1 0 0 0 0 0 4 1 0 0 0 0 0 5 1 0 0 0 0 0 6 1 0 0 0 0 0 7 0 1 0 0 0 0 8 0 1 0 0 0 0 9 0 1 0 0 0 0 10 0 1 0 0 0 0 11 0 1 0 0 0 0 12 0 1 0 0 0 0 13 0 0 1 0 0 0 14 0 0 1 0 0 0 15 0 0 1 0 0 0 16 0 0 1 0 0 0 17 0 0 1 0 0 0 18 0 0 1 0 0 0 19 0 0 0 1 0 0 20 0 0 0 1 0 0 21 0 0 0 1 0 0 22 0 0 0 1 0 0 23 0 0 0 1 0 0 24 0 0 0 1 0 0 25 0 0 0 0 1 0 26 0 0 0 0 1 0 27 0 0 0 0 1 0 28 0 0 0 0 1 0 29 0 0 0 0 1 0 30 0 0 0 0 1 0 31 0 0 0 0 0 1 32 0 0 0 0 0 1 33 0 0 0 0 0 1 34 0 0 0 0 0 1 35 0 0 0 0 0 1 36 0 0 0 0 0 1 attr(,"assign") [1] 1 1 1 1 1 1 attr(,"contrasts") attr(,"contrasts")$SITE [1] "contr.treatment" $X (Intercept) SEASONSUMMER 1 1 0 2 1 0 3 1 0 4 1 1 5 1 1 6 1 1 attr(,"assign") [1] 0 1 attr(,"contrasts") attr(,"contrasts")$SEASON [1] "contr.treatment" $nX [1] 2 $nZ [1] 6 $n [1] 36
# define parameters burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 10 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) curdies.rstan.b <- stan(data=curdies.list, model_code=rstanString, pars=c('beta','gamma','sigma','sigma_Z','sd_Resid'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.48 seconds (Warm-up) # 2.24 seconds (Sampling) # 2.72 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.39 seconds (Warm-up) # 0.94 seconds (Sampling) # 1.33 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 13000 [ 0%] (Warmup) Iteration: 1300 / 13000 [ 10%] (Warmup) Iteration: 2600 / 13000 [ 20%] (Warmup) Iteration: 3001 / 13000 [ 23%] (Sampling) Iteration: 4300 / 13000 [ 33%] (Sampling) Iteration: 5600 / 13000 [ 43%] (Sampling) Iteration: 6900 / 13000 [ 53%] (Sampling) Iteration: 8200 / 13000 [ 63%] (Sampling) Iteration: 9500 / 13000 [ 73%] (Sampling) Iteration: 10800 / 13000 [ 83%] (Sampling) Iteration: 12100 / 13000 [ 93%] (Sampling) Iteration: 13000 / 13000 [100%] (Sampling) # Elapsed Time: 0.44 seconds (Warm-up) # 0.98 seconds (Sampling) # 1.42 seconds (Total)
print(curdies.rstan.b)
Inference for Stan model: rstanString. 3 chains, each with iter=13000; warmup=3000; thin=10; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 1.09 0.00 0.17 0.77 1.00 1.09 1.18 1.44 2750 1.00 beta[2] -0.78 0.01 0.25 -1.25 -0.91 -0.79 -0.65 -0.26 2189 1.00 gamma[1] 1.11 0.00 0.13 0.85 1.01 1.11 1.19 1.37 1590 1.00 gamma[2] 1.17 0.00 0.14 0.92 1.07 1.16 1.25 1.47 1851 1.00 gamma[3] 0.99 0.00 0.14 0.68 0.91 1.00 1.09 1.26 1739 1.00 gamma[4] 0.33 0.00 0.13 0.08 0.24 0.33 0.42 0.60 1059 1.00 gamma[5] 0.25 0.00 0.13 -0.03 0.17 0.26 0.34 0.50 1228 1.00 gamma[6] 0.34 0.00 0.13 0.09 0.25 0.34 0.43 0.60 1176 1.00 sigma 0.40 0.00 0.05 0.31 0.36 0.39 0.43 0.52 1665 1.00 sigma_Z 0.19 0.01 0.18 0.03 0.07 0.14 0.24 0.64 1065 1.00 sd_Resid 0.39 0.00 0.01 0.37 0.38 0.38 0.39 0.42 2307 1.00 lp__ 22.25 0.17 4.10 13.61 19.58 22.37 25.13 29.87 560 1.01 Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:29:07 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).curdies.mcmc.e <- rstan:::as.mcmc.list.stanfit(curdies.rstan.b) curdies.mcmc.df.e <- as.data.frame(extract(curdies.rstan.b))
#Finite-population standard deviations ## Seasons seasons <- NULL seasons <- cbind(curdies.mcmc.df.e[,'beta.1'], curdies.mcmc.df.e[,'beta.1']+curdies.mcmc.df.e[,'beta.2']) sd.season <- apply(seasons,1,sd) library(coda) data.frame(mean=mean(sd.season), median=median(sd.season), HPDinterval(as.mcmc(sd.season)), HPDinterval(as.mcmc(sd.season),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.5536985 0.5585557 0.1999721 0.8859165 0.4131178 0.6909496
## Sites SD.site <- NULL sd.site <- curdies.mcmc.df.e[,3:8] for (i in 1:length(levels(curdies$SEASON))) { SD.site <- c(SD.site,apply(sd.site[,offset[i]:(offset[i+1]-1)],1,sd)) } data.frame(mean=mean(SD.site), median=median(SD.site), HPDinterval(as.mcmc(SD.site)), HPDinterval(as.mcmc(SD.site),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.1115323 0.09316411 0.001736477 0.2707392 0.01333439 0.1432832
BRM codecurdies.brm <- brm(S4DUGES ~ SEASON + (1|SITE), data=curdies, family='gaussian', prior=c(set_prior('normal(0,100)', class='b'), set_prior('cauchy(0,5)', class='sd')), n.chains=3, n.iter=2000, warmup=500, n.thin=2 )
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Chain 1, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 1, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 1, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 1, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 1, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 1, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 1, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 1, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 1, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 1, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 1, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 1, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 0.108542 seconds (Warm-up) # 0.196446 seconds (Sampling) # 0.304988 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Chain 2, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 2, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 2, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 2, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 2, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 2, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 2, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 2, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 2, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 2, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 2, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 2, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 0.104188 seconds (Warm-up) # 0.295826 seconds (Sampling) # 0.400014 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Chain 3, Iteration: 1 / 2000 [ 0%] (Warmup) Chain 3, Iteration: 200 / 2000 [ 10%] (Warmup) Chain 3, Iteration: 400 / 2000 [ 20%] (Warmup) Chain 3, Iteration: 501 / 2000 [ 25%] (Sampling) Chain 3, Iteration: 700 / 2000 [ 35%] (Sampling) Chain 3, Iteration: 900 / 2000 [ 45%] (Sampling) Chain 3, Iteration: 1100 / 2000 [ 55%] (Sampling) Chain 3, Iteration: 1300 / 2000 [ 65%] (Sampling) Chain 3, Iteration: 1500 / 2000 [ 75%] (Sampling) Chain 3, Iteration: 1700 / 2000 [ 85%] (Sampling) Chain 3, Iteration: 1900 / 2000 [ 95%] (Sampling) Chain 3, Iteration: 2000 / 2000 [100%] (Sampling) # Elapsed Time: 0.17552 seconds (Warm-up) # 0.196082 seconds (Sampling) # 0.371602 seconds (Total)
summary(curdies.brm)
Family: gaussian (identity) Formula: S4DUGES ~ SEASON + (1 | SITE) Data: curdies (Number of observations: 36) Samples: 3 chains, each with n.iter = 2000; n.warmup = 500; n.thin = 2; total post-warmup samples = 2250 WAIC: 39.88 Random Effects: ~SITE (Number of levels: 6) Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sd(Intercept) 0.18 0.16 0.01 0.62 567 1 Fixed Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept 1.09 0.17 0.74 1.45 479 1.01 SEASONSUMMER -0.79 0.22 -1.25 -0.34 713 1.00 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma(S4DUGES) 0.4 0.05 0.31 0.53 1726 1 Samples were drawn using NUTS(diag_e). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1).brms:::stancode(curdies.brm)
functions { } data { int<lower=1> N; # number of observations vector[N] Y; # response variable int<lower=1> K; # number of fixed effects matrix[N, K] X; # FE design matrix # data for random effects of SITE int<lower=1> J_1[N]; # RE levels int<lower=1> N_1; # number of levels int<lower=1> K_1; # number of REs real Z_1[N]; # RE design matrix } transformed data { } parameters { real b_Intercept; # fixed effects Intercept vector[K] b; # fixed effects vector[N_1] pre_1; # unscaled REs real<lower=0> sd_1; # RE standard deviation real<lower=0> sigma; # residual SD } transformed parameters { vector[N] eta; # linear predictor vector[N_1] r_1; # REs # compute linear predictor eta <- X * b + b_Intercept; r_1 <- sd_1 * (pre_1); # scale REs # if available add REs to linear predictor for (n in 1:N) { eta[n] <- eta[n] + Z_1[n] * r_1[J_1[n]]; } } model { # prior specifications b_Intercept ~ normal(0,100); b ~ normal(0,100); sd_1 ~ cauchy(0,5); pre_1 ~ normal(0, 1); sigma ~ cauchy(0, 5); # likelihood contribution Y ~ normal(eta, sigma); } generated quantities { }#brms:::standata(curdies.brm) - Before fully exploring the parameters, it is prudent to examine the convergence and mixing diagnostics.
Chose either any of the parameterizations (they should yield much the same) - although it is sometimes useful to explore the
different performances of effects vs matrix and JAGS vs STAN.
Full effects parameterization JAGS code
preds <- c("alpha0", "alpha[2]", "sigma", "sigma.B") plot(curdies.mcmc.a)
autocorr.diag(curdies.mcmc.a[, preds])
alpha0 alpha[2] sigma sigma.B Lag 0 1.00000000 1.000000000 1.00000000 1.0000000000 Lag 10 -0.04819928 -0.047917862 0.03408172 0.4186761852 Lag 50 -0.02022011 -0.030419011 0.00106724 0.0190520320 Lag 100 0.02621796 0.022830915 0.01421471 0.0175050583 Lag 500 0.01966791 0.004624531 -0.01605507 0.0008104889
raftery.diag(curdies.mcmc.a)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Matrix parameterization JAGS codepreds <- c("alpha[1]", "alpha[2]", "sigma", "sigma.B") plot(curdies.mcmc.b)
autocorr.diag(curdies.mcmc.b[, preds])
alpha[1] alpha[2] sigma sigma.B Lag 0 1.00000000 1.000000000 1.000000000 1.000000000 Lag 10 0.03371611 0.004028258 0.013521460 0.419591468 Lag 50 -0.01935447 0.017372840 0.006912629 0.010740829 Lag 100 -0.01690649 -0.011917936 -0.013496281 -0.012760873 Lag 500 0.02668688 -0.013412913 0.034986445 0.003179485
raftery.diag(curdies.mcmc.b)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Hierarchical parameterization JAGS codepreds <- c("beta[1]", "beta[2]", "sigma", "sigma.site") plot(curdies.mcmc.c)
autocorr.diag(curdies.mcmc.c[, preds])
beta[1] beta[2] sigma sigma.site Lag 0 1.000000000 1.000000000 1.000000000 1.000000000 Lag 10 0.021287585 0.047841790 -0.001047102 0.559956291 Lag 50 0.018520042 0.010010499 0.018111468 0.147260934 Lag 100 0.005360734 -0.011870958 0.010250879 0.007888448 Lag 500 -0.011742350 -0.008742964 0.021524966 -0.016054557
raftery.diag(curdies.mcmc.c)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Matrix parameterization STAN codelibrary(rstan) grid.arrange(stan_trace(curdies.rstan.a, pars=c('beta','sigma'), ncol=1), stan_dens(curdies.rstan.a, pars=c('beta','sigma'), separate_chains=TRUE, ncol=1), ncol=2)
stan_ac(curdies.rstan.a, pars=c('beta','sigma'))
summary(do.call(rbind, args = get_sampler_params(curdies.rstan.a, inc_warmup = FALSE)),digits = 2)
accept_stat__ stepsize__ treedepth__ n_leapfrog__ n_divergent__ Min. :0.00 Min. :0.22 Min. :1.0 Min. : 1 Min. :0.000 1st Qu.:0.80 1st Qu.:0.22 1st Qu.:3.0 1st Qu.: 7 1st Qu.:0.000 Median :0.93 Median :0.23 Median :3.0 Median : 7 Median :0.000 Mean :0.81 Mean :0.22 Mean :3.3 Mean :11 Mean :0.006 3rd Qu.:0.98 3rd Qu.:0.23 3rd Qu.:4.0 3rd Qu.:15 3rd Qu.:0.000 Max. :1.00 Max. :0.23 Max. :7.0 Max. :95 Max. :1.000
stan_diag(curdies.rstan.a)
stan_diag(curdies.rstan.a, information='stepsize')
stan_diag(curdies.rstan.a, information='treedepth')
stan_diag(curdies.rstan.a, information='divergence')
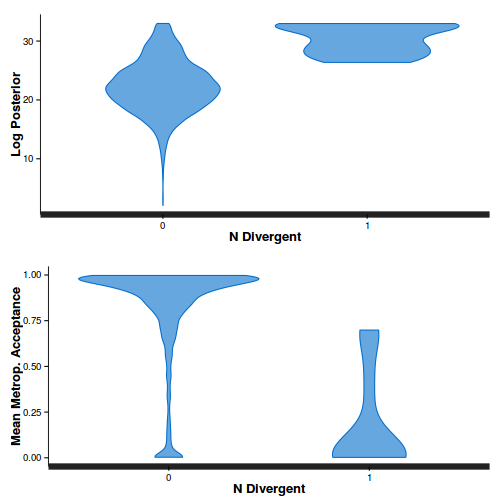
library(gridExtra) grid.arrange(stan_rhat(curdies.rstan.a)+theme_classic(8) , stan_ess(curdies.rstan.a)+theme_classic(8) , stan_mcse(curdies.rstan.a)+theme_classic(8) , ncol=2)
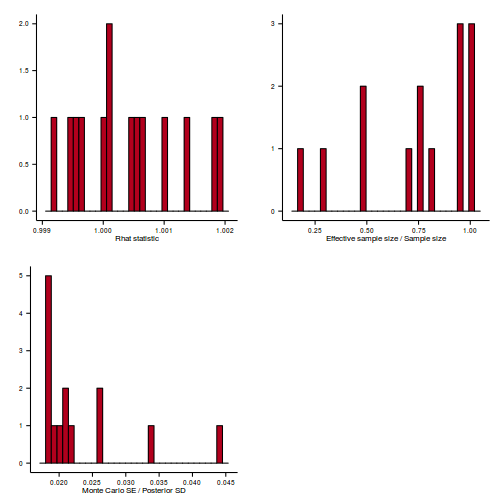
preds <- c("beta[1]", "beta[2]", "sigma", "sigma_Z") plot(curdies.mcmc.d)
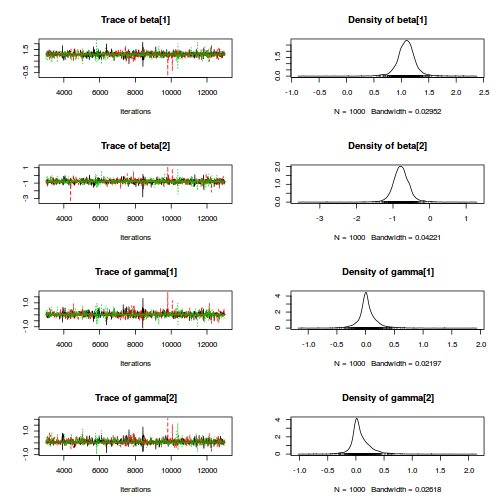
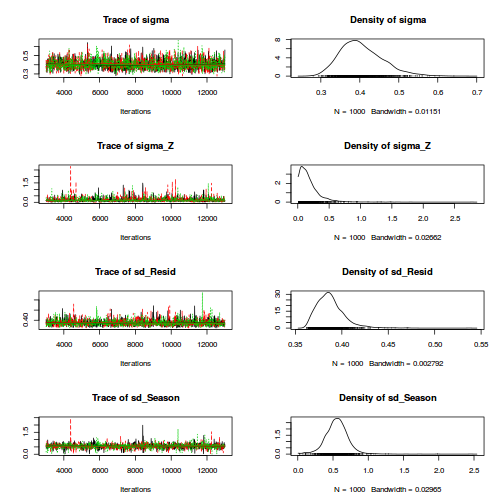
autocorr.diag(curdies.mcmc.d[, preds])
beta[1] beta[2] sigma sigma_Z Lag 0 1.000000000 1.0000000000 1.00000000 1.000000000 Lag 10 -0.003829357 -0.0001842772 0.06968841 0.232121726 Lag 50 -0.005281874 0.0092503105 0.04862283 0.060227526 Lag 100 0.013319955 0.0488246158 0.01624396 0.014919291 Lag 500 0.003200964 -0.0245307715 0.03004036 0.001269244
raftery.diag(curdies.mcmc.d)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Hierarchical parameterization STAN codepreds <- c("beta[1]", "beta[2]", "sigma", "sigma_Z") plot(curdies.mcmc.e)
autocorr.diag(curdies.mcmc.e[, preds])
beta[1] beta[2] sigma sigma_Z Lag 0 1.00000000 1.00000000 1.00000000 1.0000000000 Lag 10 0.04707077 0.07503569 0.14474725 0.1911481063 Lag 50 0.02265390 0.02383334 0.03022470 0.0512720335 Lag 100 0.02853164 0.01991633 -0.02099284 0.0055391709 Lag 500 0.03686456 0.02466837 -0.01936357 -0.0009199443
raftery.diag(curdies.mcmc.e)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
View code for BRM modellibrary(rstan) grid.arrange(stan_trace(curdies.brm$fit, pars=c('b_Intercept','b_SEASONSUMMER', 'sigma_S4DUGES'), ncol=1), stan_dens(curdies.brm$fit, pars=c('b_Intercept','b_SEASONSUMMER', 'sigma_S4DUGES'), separate_chains=TRUE, ncol=1), ncol=2)
stan_ac(stehman.brm$fit, pars=c('b_Intercept','b_SEASONSSUMMER', 'sigma_S4DUGES'))
Error in inherits(x, "stanreg"): object 'stehman.brm' not found
summary(do.call(rbind, args = get_sampler_params(curdies.brm$fit, inc_warmup = FALSE)),digits = 2)
accept_stat__ stepsize__ treedepth__ n_leapfrog__ n_divergent__ Min. :0.00 Min. :0.15 Min. :1.0 Min. : 1 Min. :0.0000 1st Qu.:0.90 1st Qu.:0.15 1st Qu.:4.0 1st Qu.:15 1st Qu.:0.0000 Median :0.97 Median :0.22 Median :4.0 Median :15 Median :0.0000 Mean :0.90 Mean :0.20 Mean :4.1 Mean :17 Mean :0.0036 3rd Qu.:0.99 3rd Qu.:0.23 3rd Qu.:4.0 3rd Qu.:15 3rd Qu.:0.0000 Max. :1.00 Max. :0.23 Max. :6.0 Max. :63 Max. :1.0000
stan_diag(curdies.brm$fit)
stan_diag(curdies.brm$fit, information='stepsize')
stan_diag(curdies.brm$fit, information='treedepth')
stan_diag(curdies.brm$fit, information='divergence')
library(gridExtra) grid.arrange(stan_rhat(curdies.brm$fit)+theme_classic(8) , stan_ess(curdies.brm$fit)+theme_classic(8) , stan_mcse(curdies.brm$fit)+theme_classic(8) , ncol=2)
- The variances in particular display substantial autocorrelation, perhaps it is worth exploring
a weekly informative Half-Cauchy prior (scale = 25) rather than a non-informative flat prior (as suggested by Gelman). It
might also be worth increasing the thinning rate from 10 to 100.
Show full effects parameterization JAGS code
modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha0 + alpha[SEASON[i]] + beta[SITE[i]] y.err[i] <- y[i]-mu[i] } #Priors alpha0 ~ dnorm(0, 1.0E-6) alpha[1] <- 0 for (i in 2:nSEASON) { alpha[i] ~ dnorm(0, 1.0E-6) #prior } for (i in 1:nSITE) { beta[i] ~ dnorm(0, tau.B) #prior } #Half-cauchy weekly informative prior (scale=25) tau <- pow(sigma,-2) sigma <- z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.B <- pow(sigma.B,-2) sigma.B <- z.B/sqrt(chSq.B) z.B ~ dnorm(0, .0016)I(0,) chSq.B ~ dgamma(0.5, 0.5) #Finite-population standard deviations for (i in 1:nSEASON) { SD.Site[i] <- sd(beta[SiteOffset[i]:SiteOffset[i+1]-1]) } sd.Season <- sd(alpha) sd.Site <- mean(SD.Site) #sd(beta.site) sd.Resid <- sd(y.err) } " writeLines(modelString,con="../downloads/BUGSscripts/ws9.2bS1.2a.txt") # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) offset
[1] 1 4 7
curdies$SITE <- factor(curdies$SITE) curdies.list <- with(curdies, list(y=S4DUGES, SITE=as.numeric(SITE), SEASON=as.numeric(SEASON), n=nrow(curdies), nSITE=length(levels(SITE)), nSEASON = length(levels(SEASON)), SiteOffset=offset ) ) # define parameters params <- c("alpha0","alpha","sigma","sigma.B","sd.Season","sd.Site","sd.Resid","SD.Site") burnInSteps = 6000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) curdies.r2jags.a <- jags(data=curdies.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.2bS1.2a.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 182 Initializing model
print(curdies.r2jags.a)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2a.txt", fit using jags, 3 chains, each with 106000 iterations (first 6000 discarded), n.thin = 100 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff SD.Site[1] 0.117 0.091 0.004 0.043 0.099 0.173 0.330 1.001 3000 SD.Site[2] 0.095 0.074 0.004 0.037 0.080 0.137 0.272 1.001 3000 alpha[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 alpha[2] -0.781 0.240 -1.198 -0.906 -0.786 -0.667 -0.306 1.001 3000 alpha0 1.091 0.179 0.753 1.008 1.091 1.181 1.405 1.004 3000 sd.Resid 0.387 0.015 0.366 0.377 0.385 0.394 0.423 1.001 3000 sd.Season 0.557 0.156 0.229 0.472 0.556 0.641 0.848 1.005 3000 sd.Site 0.106 0.071 0.005 0.050 0.096 0.153 0.260 1.001 3000 sigma 0.402 0.053 0.312 0.364 0.397 0.433 0.518 1.001 2900 sigma.B 0.179 0.196 0.006 0.067 0.130 0.227 0.641 1.001 3000 deviance 34.963 3.506 29.762 32.500 34.456 36.737 43.734 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 6.1 and DIC = 41.1 DIC is an estimate of expected predictive error (lower deviance is better).curdies.mcmc.a <- as.mcmc(curdies.r2jags.a) preds <- c("alpha0", "alpha[2]", "sigma", "sigma.B") plot(curdies.mcmc.a)
autocorr.diag(curdies.mcmc.a[, preds])
alpha0 alpha[2] sigma sigma.B Lag 0 1.000000000 1.0000000000 1.000000000 1.000000000 Lag 100 -0.010755755 -0.0540961677 -0.021166646 0.086534511 Lag 500 0.002678608 -0.0009848874 -0.008121714 -0.022853723 Lag 1000 0.033051082 0.0481177854 -0.037233461 -0.011397839 Lag 5000 -0.015636563 -0.0303283480 -0.016482653 -0.004621383
raftery.diag(curdies.mcmc.a)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Show matrix parameterization JAGS codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- inprod(alpha[],X[i,]) + beta[SITE[i]] y.err[i] <- y[i] - mu[i] } #Priors alpha ~ dmnorm(a0, A0) for (i in 1:nSITE) { beta[i] ~ dnorm(0, tau.B) #prior } #Half-cauchy weekly informative prior (scale=25) tau <- pow(sigma,-2) sigma <- z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.B <- pow(sigma.B,-2) sigma.B <- z.B/sqrt(chSq.B) z.B ~ dnorm(0, .0016)I(0,) chSq.B ~ dgamma(0.5, 0.5) # Finite-population standard deviations for (i in 1:nSEASON) { SD.Site[i] <- sd(beta[SiteOffset[i]:SiteOffset[i+1]-1]) } seasons[1] <- alpha[1] for (i in 2:nSEASON) { seasons[i] <- alpha[1]+alpha[i] } sd.Season <- sd(seasons) sd.Site <- mean(SD.Site) sd.Resid <- sd(y.err) } " writeLines(modelString,con="../downloads/BUGSscripts/ws9.2bS1.2b.txt") # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=curdies) curdies.list <- with(curdies, list(y=S4DUGES, SITE=as.numeric(SITE), X=Xmat, n=nrow(curdies), nSEASON=length(levels(SEASON)), nSITE=length(levels(SITE)), a0=rep(0, ncol(Xmat)), A0=diag(0, ncol(Xmat)), SiteOffset=offset ) ) # define parameters params <- c("alpha","sigma","sigma.B","sd.Season","sd.Site","sd.Resid","SD.Site") burnInSteps = 6000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) curdies.r2jags.b <- jags(data=curdies.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.2bS1.2b.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 264 Initializing model
print(curdies.r2jags.b)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2b.txt", fit using jags, 3 chains, each with 106000 iterations (first 6000 discarded), n.thin = 100 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff SD.Site[1] 0.117 0.091 0.003 0.043 0.099 0.174 0.329 1.001 3000 SD.Site[2] 0.093 0.074 0.003 0.034 0.077 0.137 0.275 1.001 3000 alpha[1] 1.089 0.173 0.729 1.004 1.090 1.181 1.422 1.002 3000 alpha[2] -0.782 0.256 -1.261 -0.912 -0.786 -0.660 -0.287 1.005 3000 sd.Resid 0.388 0.015 0.366 0.378 0.386 0.394 0.424 1.001 3000 sd.Season 0.558 0.165 0.219 0.467 0.556 0.645 0.899 1.001 3000 sd.Site 0.105 0.072 0.004 0.045 0.097 0.151 0.262 1.001 3000 sigma 0.401 0.052 0.314 0.364 0.397 0.434 0.520 1.001 3000 sigma.B 0.178 0.187 0.005 0.063 0.134 0.235 0.632 1.001 3000 deviance 35.048 3.356 30.013 32.736 34.495 36.882 43.176 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 5.6 and DIC = 40.7 DIC is an estimate of expected predictive error (lower deviance is better).curdies.mcmc.b <- as.mcmc(curdies.r2jags.b) preds <- c("alpha[1]", "alpha[2]", "sigma", "sigma.B") plot(curdies.mcmc.b)
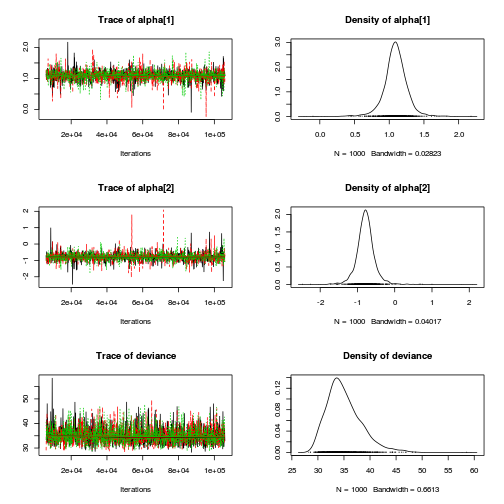
autocorr.diag(curdies.mcmc.b[, preds])
alpha[1] alpha[2] sigma sigma.B Lag 0 1.000000 1.000000 1.000000 1.000000 Lag 100 0.013155 -0.008749 -0.016552 0.060065 Lag 500 -0.001854 0.006032 -0.006479 -0.011143 Lag 1000 0.023152 -0.010042 0.012903 0.019126 Lag 5000 -0.003289 -0.009786 -0.032329 -0.004125
raftery.diag(curdies.mcmc.b)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Hierarchical parameterization JAGS codemodelString= writeLines(modelString,con="../downloads/BUGSscripts/ws9.2bS1.2c.txt") # Generate a data list curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique)) offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=ddply(curdies, ~SITE, catcolwise(unique))) curdies.list <- with(curdies, list(y=S4DUGES, SITE=as.numeric(SITE), X=Xmat, nX=ncol(Xmat), n=nrow(curdies), nSITE=length(levels(SITE)), nSEASON=length(levels(SEASON)), SiteOffset=offset ) ) # define parameters params <- c("beta","sigma","sigma.site","sd.Season","sd.Site","sd.Resid") burnInSteps = 6000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) curdies.r2jags.c <- jags(data=curdies.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.2bS1.2c.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 162 Initializing model
print(curdies.r2jags.c)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2c.txt", fit using jags, 3 chains, each with 106000 iterations (first 6000 discarded), n.thin = 100 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff beta[1] 1.089 0.172 0.755 1.000 1.090 1.180 1.395 1.002 1400 beta[2] -0.783 0.248 -1.219 -0.907 -0.790 -0.664 -0.324 1.006 1100 sd.Resid 0.387 0.015 0.366 0.378 0.386 0.393 0.423 1.001 3000 sd.Season 0.558 0.161 0.239 0.470 0.560 0.642 0.865 1.003 2200 sd.Site 0.107 0.071 0.005 0.047 0.098 0.154 0.262 1.003 1800 sigma 0.402 0.054 0.313 0.364 0.396 0.434 0.525 1.001 3000 sigma.site 0.176 0.183 0.008 0.063 0.131 0.232 0.603 1.001 3000 deviance 34.992 3.396 29.839 32.650 34.470 36.755 42.968 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 5.8 and DIC = 40.8 DIC is an estimate of expected predictive error (lower deviance is better).curdies.mcmc.c <- as.mcmc(curdies.r2jags.c) preds <- c("beta[1]", "beta[2]", "sigma", "sigma.site") plot(curdies.mcmc.c)
autocorr.diag(curdies.mcmc.c[, preds])
beta[1] beta[2] sigma sigma.site Lag 0 1.000000 1.000000 1.0000000 1.000000 Lag 100 0.011328 -0.002593 0.0001509 0.024686 Lag 500 -0.012719 -0.028442 0.0072140 -0.003313 Lag 1000 0.007359 0.005217 0.0399172 0.021000 Lag 5000 0.003469 -0.012810 0.0291639 0.007214
raftery.diag(curdies.mcmc.c)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Matrix parameterization STAN coderstanString=" data{ int n; int nZ; int nX; vector [n] y; matrix [n,nX] X; matrix [n,nZ] Z; vector [nX] a0; matrix [nX,nX] A0; } parameters{ vector [nX] beta; real<lower=0> sigma; vector [nZ] gamma; real<lower=0> sigma_Z; } transformed parameters { vector [n] mu; mu <- X*beta + Z*gamma; } model{ // Priors beta ~ multi_normal(a0,A0); gamma ~ normal( 0 , sigma_Z ); sigma_Z ~ cauchy(0,25); sigma ~ cauchy(0,25); y ~ normal( mu , sigma ); } generated quantities { vector [n] y_err; real<lower=0> sd_Resid; y_err <- y - mu; sd_Resid <- sd(y_err); } " # Generate a data list curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=curdies) Zmat <- model.matrix(~-1+SITE, data=curdies) curdies.list <- with(curdies, list(y=S4DUGES, Z=Zmat, X=Xmat, nX=ncol(Xmat), nZ=ncol(Zmat), n=nrow(curdies), a0=rep(0,ncol(Xmat)), A0=diag(100000,ncol(Xmat)) ) ) # define parameters burnInSteps = 6000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) curdies.rstan.a <- stan(data=curdies.list, model_code=rstanString, pars=c('beta','gamma','sigma','sigma_Z', 'sd_Resid'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.81 seconds (Warm-up) # 21.03 seconds (Sampling) # 21.84 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.85 seconds (Warm-up) # 15.14 seconds (Sampling) # 15.99 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.83 seconds (Warm-up) # 15.24 seconds (Sampling) # 16.07 seconds (Total)
print(curdies.rstan.a)
Inference for Stan model: rstanString. 3 chains, each with iter=106000; warmup=6000; thin=100; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 1.09 0.00 0.18 0.77 1.00 1.09 1.18 1.43 2224 1 beta[2] -0.79 0.01 0.25 -1.27 -0.92 -0.79 -0.66 -0.32 2202 1 gamma[1] 0.01 0.00 0.18 -0.31 -0.05 0.01 0.08 0.37 2644 1 gamma[2] 0.08 0.00 0.19 -0.24 -0.01 0.04 0.15 0.47 2786 1 gamma[3] -0.10 0.00 0.19 -0.53 -0.18 -0.06 0.00 0.18 2588 1 gamma[4] 0.02 0.00 0.18 -0.30 -0.04 0.01 0.09 0.37 3000 1 gamma[5] -0.05 0.00 0.18 -0.43 -0.12 -0.03 0.02 0.27 3000 1 gamma[6] 0.04 0.00 0.18 -0.27 -0.04 0.02 0.10 0.42 3000 1 sigma 0.40 0.00 0.05 0.31 0.37 0.40 0.44 0.52 2934 1 sigma_Z 0.19 0.00 0.21 0.02 0.07 0.14 0.24 0.68 2542 1 sd_Resid 0.39 0.00 0.02 0.37 0.38 0.39 0.39 0.43 1517 1 lp__ 22.62 0.11 4.60 13.78 19.56 22.38 25.45 32.09 1605 1 Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:31:25 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).curdies.mcmc.d <- rstan:::as.mcmc.list.stanfit(curdies.rstan.a) curdies.mcmc.df.d <- as.data.frame(extract(curdies.rstan.a)) preds <- c("beta[1]", "beta[2]", "sigma", "sigma_Z") plot(curdies.mcmc.d)
autocorr.diag(curdies.mcmc.d[, preds])
beta[1] beta[2] sigma sigma_Z Lag 0 1.000000 1.00000 1.000000 1.000000 Lag 100 0.049602 0.03405 0.011961 0.040739 Lag 500 0.001999 0.01131 -0.003834 -0.009070 Lag 1000 0.001019 -0.01372 0.022460 0.027303 Lag 5000 0.023995 0.01447 0.001216 -0.007945
raftery.diag(curdies.mcmc.d)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
#Finite-population standard deviations ## Site curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) sites<-ddply(curdies, ~SITE, catcolwise(unique))
Error in eval(expr, envir, enclos): could not find function "ddply"
offset <- c(match(levels(sites$SEASON),sites$SEASON), length(sites$SEASON)+1) SD.site <- NULL sd.site <- curdies.mcmc.df.d[,3:8] for (i in 1:length(levels(curdies$SEASON))) { SD.site <- c(SD.site,apply(sd.site[,offset[i]:(offset[i+1]-1)],1,sd)) } data.frame(mean=mean(SD.site), median=median(SD.site), HPDinterval(as.mcmc(SD.site)), HPDinterval(as.mcmc(SD.site),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.1091143 0.09009361 0.001057878 0.2720609 0.007046607 0.1374872
#Season seasons <- NULL seasons <- cbind(curdies.mcmc.df.d[,'beta.1'], curdies.mcmc.df.d[,'beta.1']+curdies.mcmc.df.d[,'beta.2']) sd.season <- apply(seasons,1,sd) library(coda) data.frame(mean=mean(sd.season), median=median(sd.season), HPDinterval(as.mcmc(sd.season)), HPDinterval(as.mcmc(sd.season),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.5604005 0.5600543 0.2238934 0.8789284 0.4244865 0.701144
Hierarchical parameterization STAN coderstanString=" data{ int n; int nZ; int nX; vector [n] y; matrix [nZ,nX] X; matrix [n,nZ] Z; } parameters{ vector [nX] beta; real<lower=0> sigma; vector [nZ] gamma; real<lower=0> sigma_Z; } transformed parameters { vector [n] mu_Z; vector [nZ] mu; mu_Z <- Z*gamma; mu <- X*beta; } model{ // Priors beta ~ normal(0, 10000); gamma ~ normal( 0 , 1000); sigma_Z ~ uniform( 0 , 100 ); sigma ~ uniform( 0 , 100 ); y ~ normal(mu_Z, sigma); gamma ~ normal( mu , sigma_Z ); } generated quantities { vector [n] y_err; real<lower=0> sd_Resid; y_err <- y - mu_Z; sd_Resid <- sd(y_err); } " # Generate a data list curdies$SITE <- factor(curdies$SITE) Xmat <- model.matrix(~SEASON, data=ddply(curdies, ~SITE, catcolwise(unique))) Zmat <- model.matrix(~-1+SITE, data=curdies) curdies.list <- with(curdies, list(y=S4DUGES, Z=Zmat, X=Xmat, nX=ncol(Xmat), nZ=ncol(Zmat), n=nrow(curdies) ) ) curdies.list
$y [1] 0.8971 1.5713 1.0700 1.1461 1.0991 1.0141 1.0040 2.0061 1.0396 1.0060 1.1909 1.3845 0.9111 1.0508 1.0272 0.9003 0.6074 0.7104 0.0000 0.0000 0.9849 0.0000 0.0000 1.1200 1.0828 0.0000 0.0000 0.0000 [29] 0.0000 0.0000 0.0000 0.0000 0.6038 0.0000 0.9007 0.7823 $Z SITE1 SITE2 SITE3 SITE4 SITE5 SITE6 1 1 0 0 0 0 0 2 1 0 0 0 0 0 3 1 0 0 0 0 0 4 1 0 0 0 0 0 5 1 0 0 0 0 0 6 1 0 0 0 0 0 7 0 1 0 0 0 0 8 0 1 0 0 0 0 9 0 1 0 0 0 0 10 0 1 0 0 0 0 11 0 1 0 0 0 0 12 0 1 0 0 0 0 13 0 0 1 0 0 0 14 0 0 1 0 0 0 15 0 0 1 0 0 0 16 0 0 1 0 0 0 17 0 0 1 0 0 0 18 0 0 1 0 0 0 19 0 0 0 1 0 0 20 0 0 0 1 0 0 21 0 0 0 1 0 0 22 0 0 0 1 0 0 23 0 0 0 1 0 0 24 0 0 0 1 0 0 25 0 0 0 0 1 0 26 0 0 0 0 1 0 27 0 0 0 0 1 0 28 0 0 0 0 1 0 29 0 0 0 0 1 0 30 0 0 0 0 1 0 31 0 0 0 0 0 1 32 0 0 0 0 0 1 33 0 0 0 0 0 1 34 0 0 0 0 0 1 35 0 0 0 0 0 1 36 0 0 0 0 0 1 attr(,"assign") [1] 1 1 1 1 1 1 attr(,"contrasts") attr(,"contrasts")$SITE [1] "contr.treatment" $X (Intercept) SEASONSUMMER 1 1 0 2 1 0 3 1 0 4 1 1 5 1 1 6 1 1 attr(,"assign") [1] 0 1 attr(,"contrasts") attr(,"contrasts")$SEASON [1] "contr.treatment" $nX [1] 2 $nZ [1] 6 $n [1] 36
# define parameters burnInSteps = 6000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) curdies.rstan.b <- stan(data=curdies.list, model_code=rstanString, pars=c('beta','gamma','sigma','sigma_Z','sd_Resid'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.7 seconds (Warm-up) # 11.92 seconds (Sampling) # 12.62 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.73 seconds (Warm-up) # 16.12 seconds (Sampling) # 16.85 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.74 seconds (Warm-up) # 16.8 seconds (Sampling) # 17.54 seconds (Total)
print(curdies.rstan.b)
Inference for Stan model: rstanString. 3 chains, each with iter=106000; warmup=6000; thin=100; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 1.09 0.00 0.19 0.72 1.01 1.09 1.18 1.41 2882 1 beta[2] -0.78 0.00 0.27 -1.22 -0.92 -0.79 -0.66 -0.33 2879 1 gamma[1] 1.11 0.00 0.13 0.85 1.03 1.11 1.19 1.37 2668 1 gamma[2] 1.17 0.00 0.14 0.91 1.08 1.17 1.26 1.47 2491 1 gamma[3] 0.99 0.00 0.15 0.69 0.90 1.00 1.09 1.25 2716 1 gamma[4] 0.32 0.00 0.13 0.06 0.24 0.32 0.41 0.60 2799 1 gamma[5] 0.25 0.00 0.14 -0.04 0.16 0.25 0.34 0.50 2904 1 gamma[6] 0.34 0.00 0.13 0.09 0.26 0.34 0.42 0.61 2844 1 sigma 0.40 0.00 0.05 0.31 0.37 0.40 0.43 0.52 2690 1 sigma_Z 0.19 0.00 0.20 0.03 0.08 0.14 0.25 0.64 2545 1 sd_Resid 0.39 0.00 0.01 0.37 0.38 0.38 0.39 0.42 3000 1 lp__ 22.16 0.11 4.11 13.75 19.57 22.15 24.82 30.24 1372 1 Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:32:40 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).curdies.mcmc.e <- rstan:::as.mcmc.list.stanfit(curdies.rstan.b) curdies.mcmc.df.e <- as.data.frame(extract(curdies.rstan.b)) preds <- c("beta[1]", "beta[2]", "sigma", "sigma_Z") plot(curdies.mcmc.e)
autocorr.diag(curdies.mcmc.e[, preds])
beta[1] beta[2] sigma sigma_Z Lag 0 1.000000 1.000000 1.000000 1.000000 Lag 100 0.005039 0.020794 0.034445 0.039067 Lag 500 0.010435 -0.009136 -0.010605 0.001239 Lag 1000 0.008577 0.010613 0.015420 -0.015927 Lag 5000 0.015266 0.022877 -0.008721 0.003651
raftery.diag(curdies.mcmc.e)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
#Finite-population standard deviations ## Seasons seasons <- NULL seasons <- cbind(curdies.mcmc.df.e[,'beta.1'], curdies.mcmc.df.e[,'beta.1']+curdies.mcmc.df.e[,'beta.2']) sd.season <- apply(seasons,1,sd) library(coda) data.frame(mean=mean(sd.season), median=median(sd.season), HPDinterval(as.mcmc(sd.season)), HPDinterval(as.mcmc(sd.season),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.5614793 0.558442 0.2493118 0.8651797 0.4270324 0.6952875
## Sites SD.site <- NULL sd.site <- curdies.mcmc.df.e[,3:8] for (i in 1:length(levels(curdies$SEASON))) { SD.site <- c(SD.site,apply(sd.site[,offset[i]:(offset[i+1]-1)],1,sd)) } data.frame(mean=mean(SD.site), median=median(SD.site), HPDinterval(as.mcmc(SD.site)), HPDinterval(as.mcmc(SD.site),p=0.68))
mean median lower upper lower.1 upper.1 var1 0.1134773 0.09522703 0.00400208 0.2749261 0.01109254 0.1420809
- Explore the parameter estimates
Full effects parameterization JAGS code
library(R2jags) print(curdies.r2jags.a)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2a.txt", fit using jags, 3 chains, each with 106000 iterations (first 6000 discarded), n.thin = 100 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff SD.Site[1] 0.117 0.091 0.004 0.043 0.099 0.173 0.330 1.001 3000 SD.Site[2] 0.095 0.074 0.004 0.037 0.080 0.137 0.272 1.001 3000 alpha[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 alpha[2] -0.781 0.240 -1.198 -0.906 -0.786 -0.667 -0.306 1.001 3000 alpha0 1.091 0.179 0.753 1.008 1.091 1.181 1.405 1.004 3000 sd.Resid 0.387 0.015 0.366 0.377 0.385 0.394 0.423 1.001 3000 sd.Season 0.557 0.156 0.229 0.472 0.556 0.641 0.848 1.005 3000 sd.Site 0.106 0.071 0.005 0.050 0.096 0.153 0.260 1.001 3000 sigma 0.402 0.053 0.312 0.364 0.397 0.433 0.518 1.001 2900 sigma.B 0.179 0.196 0.006 0.067 0.130 0.227 0.641 1.001 3000 deviance 34.963 3.506 29.762 32.500 34.456 36.737 43.734 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 6.1 and DIC = 41.1 DIC is an estimate of expected predictive error (lower deviance is better).Full effects parameterization JAGS codeprint(curdies.r2jags.b)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2b.txt", fit using jags, 3 chains, each with 106000 iterations (first 6000 discarded), n.thin = 100 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff SD.Site[1] 0.117 0.091 0.003 0.043 0.099 0.174 0.329 1.001 3000 SD.Site[2] 0.093 0.074 0.003 0.034 0.077 0.137 0.275 1.001 3000 alpha[1] 1.089 0.173 0.729 1.004 1.090 1.181 1.422 1.002 3000 alpha[2] -0.782 0.256 -1.261 -0.912 -0.786 -0.660 -0.287 1.005 3000 sd.Resid 0.388 0.015 0.366 0.378 0.386 0.394 0.424 1.001 3000 sd.Season 0.558 0.165 0.219 0.467 0.556 0.645 0.899 1.001 3000 sd.Site 0.105 0.072 0.004 0.045 0.097 0.151 0.262 1.001 3000 sigma 0.401 0.052 0.314 0.364 0.397 0.434 0.520 1.001 3000 sigma.B 0.178 0.187 0.005 0.063 0.134 0.235 0.632 1.001 3000 deviance 35.048 3.356 30.013 32.736 34.495 36.882 43.176 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 5.6 and DIC = 40.7 DIC is an estimate of expected predictive error (lower deviance is better).Hierarchical parameterization JAGS codeprint(curdies.r2jags.c)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.2bS1.2c.txt", fit using jags, 3 chains, each with 106000 iterations (first 6000 discarded), n.thin = 100 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff beta[1] 1.089 0.172 0.755 1.000 1.090 1.180 1.395 1.002 1400 beta[2] -0.783 0.248 -1.219 -0.907 -0.790 -0.664 -0.324 1.006 1100 sd.Resid 0.387 0.015 0.366 0.378 0.386 0.393 0.423 1.001 3000 sd.Season 0.558 0.161 0.239 0.470 0.560 0.642 0.865 1.003 2200 sd.Site 0.107 0.071 0.005 0.047 0.098 0.154 0.262 1.003 1800 sigma 0.402 0.054 0.313 0.364 0.396 0.434 0.525 1.001 3000 sigma.site 0.176 0.183 0.008 0.063 0.131 0.232 0.603 1.001 3000 deviance 34.992 3.396 29.839 32.650 34.470 36.755 42.968 1.001 3000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 5.8 and DIC = 40.8 DIC is an estimate of expected predictive error (lower deviance is better).Full matrix parameterization STAN codeprint(curdies.rstan.a)
Inference for Stan model: rstanString. 3 chains, each with iter=106000; warmup=6000; thin=100; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 1.09 0.00 0.18 0.77 1.00 1.09 1.18 1.43 2224 1 beta[2] -0.79 0.01 0.25 -1.27 -0.92 -0.79 -0.66 -0.32 2202 1 gamma[1] 0.01 0.00 0.18 -0.31 -0.05 0.01 0.08 0.37 2644 1 gamma[2] 0.08 0.00 0.19 -0.24 -0.01 0.04 0.15 0.47 2786 1 gamma[3] -0.10 0.00 0.19 -0.53 -0.18 -0.06 0.00 0.18 2588 1 gamma[4] 0.02 0.00 0.18 -0.30 -0.04 0.01 0.09 0.37 3000 1 gamma[5] -0.05 0.00 0.18 -0.43 -0.12 -0.03 0.02 0.27 3000 1 gamma[6] 0.04 0.00 0.18 -0.27 -0.04 0.02 0.10 0.42 3000 1 sigma 0.40 0.00 0.05 0.31 0.37 0.40 0.44 0.52 2934 1 sigma_Z 0.19 0.00 0.21 0.02 0.07 0.14 0.24 0.68 2542 1 sd_Resid 0.39 0.00 0.02 0.37 0.38 0.39 0.39 0.43 1517 1 lp__ 22.62 0.11 4.60 13.78 19.56 22.38 25.45 32.09 1605 1 Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:31:25 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).Hierarchical parameterization STAN codeprint(curdies.rstan.b)
Inference for Stan model: rstanString. 3 chains, each with iter=106000; warmup=6000; thin=100; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 1.09 0.00 0.19 0.72 1.01 1.09 1.18 1.41 2882 1 beta[2] -0.78 0.00 0.27 -1.22 -0.92 -0.79 -0.66 -0.33 2879 1 gamma[1] 1.11 0.00 0.13 0.85 1.03 1.11 1.19 1.37 2668 1 gamma[2] 1.17 0.00 0.14 0.91 1.08 1.17 1.26 1.47 2491 1 gamma[3] 0.99 0.00 0.15 0.69 0.90 1.00 1.09 1.25 2716 1 gamma[4] 0.32 0.00 0.13 0.06 0.24 0.32 0.41 0.60 2799 1 gamma[5] 0.25 0.00 0.14 -0.04 0.16 0.25 0.34 0.50 2904 1 gamma[6] 0.34 0.00 0.13 0.09 0.26 0.34 0.42 0.61 2844 1 sigma 0.40 0.00 0.05 0.31 0.37 0.40 0.43 0.52 2690 1 sigma_Z 0.19 0.00 0.20 0.03 0.08 0.14 0.25 0.64 2545 1 sd_Resid 0.39 0.00 0.01 0.37 0.38 0.38 0.39 0.42 3000 1 lp__ 22.16 0.11 4.11 13.75 19.57 22.15 24.82 30.24 1372 1 Samples were drawn using NUTS(diag_e) at Sun Mar 8 15:32:40 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).BRM codesummary(curdies.brm)
Family: gaussian (identity) Formula: S4DUGES ~ SEASON + (1 | SITE) Data: curdies (Number of observations: 36) Samples: 3 chains, each with n.iter = 2000; n.warmup = 500; n.thin = 2; total post-warmup samples = 2250 WAIC: 39.88 Random Effects: ~SITE (Number of levels: 6) Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sd(Intercept) 0.18 0.16 0.01 0.62 567 1 Fixed Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept 1.09 0.17 0.74 1.45 479 1.01 SEASONSUMMER -0.79 0.22 -1.25 -0.34 713 1.00 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma(S4DUGES) 0.4 0.05 0.31 0.53 1726 1 Samples were drawn using NUTS(diag_e). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1). - How about that summary figure then?
Matrix parameterization JAGS code
preds <- c('beta[1]','beta[2]') coefs <- curdies.r2jags.c$BUGSoutput$sims.matrix[,preds] curdies$SEASON <- factor(curdies$SEASON, levels=c("WINTER","SUMMER")) newdata <- data.frame(SEASON=levels(curdies$SEASON)) Xmat <- model.matrix(~SEASON, newdata) pred <- coefs %*% t(Xmat) library(plyr) newdata <- cbind(newdata, adply(pred, 2, function(x) { data.frame(Median=median(x)^4, HPDinterval(as.mcmc(x))^4, HPDinterval(as.mcmc(x), p=0.68)^4) })) newdata
SEASON X1 Median lower upper lower.1 upper.1 1 WINTER 1 0.008805 1.235e-07 0.1335 0.0006134 0.03213 2 SUMMER 2 1.412530 3.190e-01 3.7407 0.8355808 2.23421
library(ggplot2) p1 <- ggplot(newdata, aes(y=Median, x=SEASON)) + geom_linerange(aes(ymin=lower, ymax=upper), show_guide=FALSE)+ geom_linerange(aes(ymin=lower.1, ymax=upper.1), size=2,show_guide=FALSE)+ geom_point(size=4, shape=21, fill="white")+ scale_y_sqrt('Number of Dugesia per stone')+ theme_classic()+ theme(axis.title.y=element_text(vjust=2,size=rel(1.2)), axis.title.x=element_text(vjust=-2,size=rel(1.2)), plot.margin=unit(c(0.5,0.5,2,2), 'lines')) preds <- c('sd.Resid','sd.Site','sd.Season') curdies.sd <- adply(curdies.r2jags.c$BUGSoutput$sims.matrix[,preds],2,function(x) { data.frame(mean=mean(x), median=median(x), HPDinterval(as.mcmc(x)), HPDinterval(as.mcmc(x),p=0.68)) }) head(curdies.sd)
X1 mean median lower upper lower.1 upper.1 1 sd.Resid 0.3874 0.38556 0.3641406 0.4154 0.3720475 0.3955 2 sd.Site 0.1065 0.09773 0.0001281 0.2356 0.0007675 0.1368 3 sd.Season 0.5578 0.55956 0.2393835 0.8659 0.4214354 0.6854
rownames(curdies.sd) <- c("Residuals", "Site", "Season") curdies.sd$name <- factor(c("Residuals", "Site", "Season"), levels=c("Residuals", "Site", "Season")) curdies.sd$Perc <- curdies.sd$median/sum(curdies.sd$median) p2<-ggplot(curdies.sd,aes(y=name, x=median))+ geom_vline(xintercept=0,linetype="dashed")+ geom_hline(xintercept=0)+ scale_x_continuous("Finite population \nvariance components (sd)")+ geom_errorbarh(aes(xmin=lower.1, xmax=upper.1), height=0, size=1)+ geom_errorbarh(aes(xmin=lower, xmax=upper), height=0, size=1.5)+ geom_point(size=3, shape=21, fill='white')+ geom_text(aes(label=sprintf("(%4.1f%%)",Perc),vjust=-1))+ theme_classic()+ theme(axis.title.y=element_blank(), axis.text.y=element_text(size=rel(1.2),hjust=1)) library(gridExtra) grid.arrange(p1,p2,ncol=2)
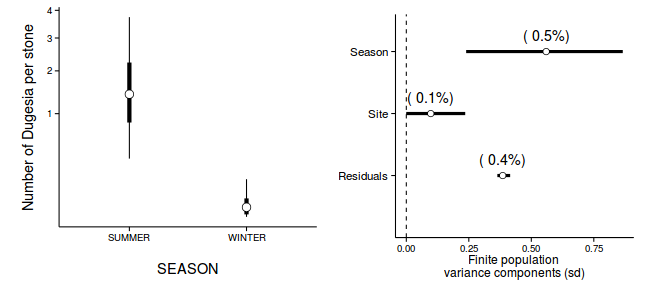
Exploratory data analysis has indicated that the response variable could be normalized via a forth-root transformation.
References
[1] A. Gelman. "Prior distributions for variance parameters in hierarchical models". In: _Bayesian Analysis_ (2006), pp. 515-533.
