Tutorial 7.1 - Introduction to linear models
04 Jun 2017
Statistical models
A statistical model is an expression that attempts to explain patterns in the observed values of a response variable by relating the response variable to a set of predictor variables and parameters. Consider the following familiar mathematical model: $$y=mx+c$$ or equivalently, $$y=a+bx$$
This simple mathematical model relates a response variable ($y$) to a single predictor variable ($x$)
as a straight line according to the values of two constant parameters:
|
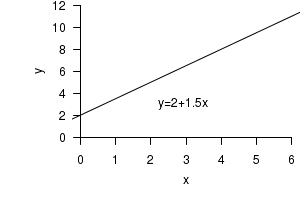 |
The above model represents a perfect fit, that is, 100% of the change (variation) in $y$ is explained by a change in $x$. However, rarely would this be the case when modeling biological variables. In complex biological systems, variables are typically the result of many influential and interacting factors and therefore simple models usually fail to fully explain a response variable. The statistical model is distinguished from a mathematical model by the presence of an error component that represents the portion of the response variable that the model fails to explain. In a statistical model, the error component is usually assumed to be drawn from a specific distribution (typically a normal or Gaussian distribution).
Hence, statistical models are of the form: $${response~variable} = model + error$$ where the $model$ component comprises of one or more categorical and/or continuous predictor variable(s) and their parameter(s) that together represent the effect of the predictors variable(s) on the mean the response variable. The $error$ component represents the "noise" in the model. That is, it represents the differences between the observed responses and the responses predicted by the model component.
In statistical speak, the above is usually expressed as: $$response = {deterministic~component} + {stochastic~component}$$ or $$response = {systematic~component} + {stochastic~component}$$ reflecting that the exact value of a given observation of $y$ depends on both the measured influences (deterministic or systematic component) and other unmeasured, random influences (stochastic component).
A parameter and its associated predictor variable(s) are referred to as a model term. A statistical model is fitted to observed data so as to estimate the model parameters and test hypotheses about these parameters (coefficients).
Linear models
Linear models are those statistical models in which a series of predictors and their associated parameters are arranged as a linear combination. That is, within the model, no predictor appears as either a multiplier, divisor or exponent to any other predictor. Importantly, the term "linear" in this context does not pertain to the nature of the relationship between the response variable and the predictor variable(s), and thus linear models are not restricted to "linear" (straight-line) relationships. Collectively, a linear combination of predictors and associated parameters are also known as the linear predictor.
An example of a very simple linear model is the model used to investigate the linear relationship between a continuous response variable ($Y$ and a single continuous predictor variable, $X$): $$ \begin{alignat*}{2} y_i=&\qquad\qquad\beta_0\qquad\qquad+ \qquad\qquad\beta_1\quad\qquad\times \qquad\qquad x_i \qquad\qquad + \qquad\qquad\epsilon_i\\ {response~variable}=&\underbrace{\underbrace{\qquad\begin{matrix}population\\intercept\end{matrix}\qquad}_\text{intercept term} + \underbrace{\qquad\begin{matrix}population\\slope\end{matrix}\qquad \times \qquad\begin{matrix}predictor\\variable\end{matrix}\qquad}_\text{slope term}}_\text{systematic component = linear predictor}\qquad + \qquad \underbrace{\qquad error\qquad }_\text{Stochastic component} \end{alignat*} $$
The above notation is typical of that used to represent the elements of a linear model.
- $y$ denotes the response variable and $x$ represents the predictor variable.
- The subscript ($i$) is used to represent a set of observations (usually from 1 to $n$ where $n$ is the total sample size) and thus $y_i$ and $x_i$ represent respectively the $i$th observation of the $Y$ and $X$ variables.
- $\varepsilon_i$ represents the deviation of the $i$th observed $Y$ from the value of $Y$ expected by the model component.
- The parameters $\beta_0$ and $\beta_1$ represent population intercept and population slope (effect of $X$ on $Y$ per unit of $x$) respectively. Population (effect) parameters are usually represented by Greek symbols.
To appreciate this more fully, consider the following fabricated data.
|
\begin{alignat*}{4}
0\quad&=\quad&\beta_0\times 1\quad&+\quad&\beta_1\times 1\quad&+\quad&\varepsilon_1\\
1\quad&=\quad&\beta_0\times 1\quad&+\quad&\beta_1\times 2\quad&+\quad&\varepsilon_2\\
2\quad&=\quad&\beta_0\times 1\quad&+\quad&\beta_1\times 3\quad&+\quad&\varepsilon_3\\
4\quad&=\quad&\beta_0\times 1\quad&+\quad&\beta_1\times 4\quad&+\quad&\varepsilon_4\\
7\quad&=\quad&\beta_0\times 1\quad&+\quad&\beta_1\times 5\quad&+\quad&\varepsilon_5\\
10\quad&=\quad&\beta_0\times 1\quad&+\quad&\beta_1\times 6\quad&+\quad&\varepsilon_6\\
\end{alignat*}
|
The above can be represented in matrix notation: $$\underbrace{\begin{pmatrix} 0\\1\\2\\4\\7\\10 \end{pmatrix}}_\text{Response values} = \underbrace{\begin{pmatrix} 1&1\\1&2\\1&3\\1&4\\1&5\\1&6 \end{pmatrix}}_\text{Model matrix} \times \underbrace{\begin{pmatrix} \beta_0\\\beta_1 \end{pmatrix}}_\text{Parameter vector} + \underbrace{\begin{pmatrix} \varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\varepsilon_4&\\\varepsilon_5\\\varepsilon_6 \end{pmatrix}}_\text{Residual vector} $$ The model matrix (also known as the design matrix) contains the "weights" for each parameter for each of the sampling units. The above matrix notation also isolates and thus highlights the "unknown" regression parameters (\$beta_0$ and $\beta_1$) from the observed data from which they are estimated.
When there are multiple continuous predictor variables, in addition to the intercept parameter ($\beta_0$), the linear model includes a separate slope parameter for each of the predictor variables: $$y_i=\beta_0+\beta_1x1_i+\beta_2x2_i+...+\varepsilon_i$$
The model structure for linear models containing a single categorical predictor variable (known as a factor) with two or more treatment levels (groups) is similar in form to the multiple linear regression model (listed immediately above) with the overall mean ($\mu$) replacing the y-intercept ($\beta_0$). The factor levels (groups) are represented in the model by binary (contain only of 0s and 1s, see Table below) indicator (or `dummy') variables and their associated estimable parameters ($\beta_1,~\beta_2,~...$).
For a data set comprising of $p$ groups and $n$ replicates within each group, the linear model is: $$y_{ij} = \mu + \beta_1(dummy_1)_{ij} + \beta_2(dummy_2)_{ij} + .... + \varepsilon_{ij}$$ where $i$ represents the treatment levels (from 1 to $p$) and $j$ represents the set of replicates (from 1 to $n$) within the $i^{th}$ group. Hence, $y_{ij}$ represents the $j^{th}$ observation of the response variable within the $i^{th}$ group and $(dummy_1)_{ij}$ represents the dummy code for the $j^{th}$ replicate within the $i^{th}$ group of the first dummy variable (first treatment level).
| Raw data | Dummy coded data | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
The dummy variable for a particular treatment level contains all 0s except in the rows that correspond to observations that received that treatment level. The table above illustrates the dummy coding for a single factor with three levels (`G1', `G2', `G3') each with three replicates. Note that a linear model of the form: $$y_{ij}=\mu+\beta_1(dummy_1)_{ij} + \beta_2(dummy_2)_{ij} +\beta_3(dummy_3)_{ij} + \varepsilon_{ij}$$ is over-parameterized (as we are attempting to estimate four parameters from three populations, see Estimation).
More typically however, statistical models that include one or more factors (categorical variables) are expressed as effects models in which the individual treatment levels (and their parameters) are represented by a single term (e.g. $\alpha_i$) that denotes the effect of each of the levels of the factor on the overall mean. Specifically, an effect is the difference between the treatment group and some reference (such as the overall mean or another treatment group). For a data set comprised of $p$ groups and $n$ replicates within each group, the linear effects model is: $$y_{ij} = \mu + \alpha_{i} + \varepsilon_{ij}$$ where $i$ represents the set of treatments (from 1 to $p$) and $j$ represents the set of replicates (from 1 to $n$) within the $i^{th}$ group. Hence, $y_{ij}$ represents the $j^{th}$ observation of the response variable within the $i^{th}$ group of the factor.
- $\mu$ is the overall population mean of the response variable ($Y$) and is equivalent to the intercept.
- $\alpha_i$ represents the effect of the $i^{th}$ group calculated as the difference between each of the group means and the overall mean ($\alpha_i=\mu_i - \mu$).
Linear models in R
Statistical models in R are represented by a formula corresponding to the linear model (for continuous variables) or effects model (categorical variables):
response∼model
where the tilde (∼) defines a model formula and model represents a set of terms to include in the model.
Terms are included in a model via their variable names and terms preceded by the - (negative sign) operator are explicitly excluded.
The intercept term (denoted by a 1) is implicit in the model and need not be specified.
Hence the following model formulae all model the effect of the variable $X$ on the $Y$ variable with the inclusion of the intercept:
Y~X Y~1+X
Y~-1+X Y~X-1
Linear models are fitted by providing the model formula as an argument to the lm() function. To fit the simple linear regression model relating a fictitious response variable ($Y$) to fictitious continuous predictor variable ($X$):
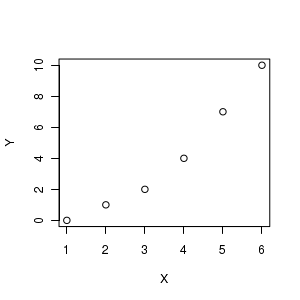
#construct some data Y<-c(0,1,2,4,7,10) X<-1:6 #Explore the relationship graphically plot(Y~X) # fit the linear model Fictitious.lm <- lm(Y~X) |
 |
summary(Fictitious.lm)
Call:
lm(formula = Y ~ X)
Residuals:
1 2 3 4 5 6
1.000e+00 -6.661e-16 -1.000e+00 -1.000e+00 -5.551e-17 1.000e+00
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.0000 0.9309 -3.223 0.03220 *
X 2.0000 0.2390 8.367 0.00112 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 4 degrees of freedom
Multiple R-squared: 0.9459, Adjusted R-squared: 0.9324
F-statistic: 70 on 1 and 4 DF, p-value: 0.001116
- The summary output begins by specifying the nature of the call used to fit the model.
- Next is a summary of the residuals (differences between observed responses and expected responses for each value of the predictor variable).
- The estimated parameters are listed in the coefficients table.
- Each row of the table lists the value of an estimated parameter from the linear model along with the outcome of a hypothesis test for this parameter.
- The row labeled (Intercept) concerns the intercept (overall constant) and subsequent rows are labeled according to the model term that is associated with the estimated parameter. In this case, the row labeled X concerns the population slope ($\beta_1$).
- Finally a brief summary of the partitioning of total variation (ANOVA, see Hypothesis testing) in the response variable is provided.
Estimating linear model parameters
During model fitting, parameters can be estimated using any of the estimation methods outlined in Tutorial 4.3, although ordinary least squares (OLS) and maximum likelihood (ML or REML) are the most common.
The OLS approach estimates the value of one or more parameters such that they minimize the sum of squared deviations between the observed values and the values expected by the model and will be illustrated in detail in the following sections.
Models that utilize OLS parameter estimates are referred to as `general' linear models as they accommodate both continuous and categorical predictor variables. Broadly speaking, such models that incorporate purely continuous predictor variables are referred to as `regression' models whereas models that purely incorporate categorical predictors are called `ANOVA' models. Analysis of covariance (ANCOVA) models incorporate both categorical and continuous predictor variables
ML estimators estimate one or more population parameters such that the (log) likelihood of obtaining the observed values from such populations is maximized. ML estimators are useful when there is evidence of a relationship between mean and variance or for models involving correlated data structures.
Maximum likelihood parameter estimation is also utilized by `generalized' linear models, so called as they are not restricted to normally distributed response and residuals. Generalized linear models accommodate any exponential probability distribution (including normal, binomial, Poisson, gamma and negative binomial) - it is the exponential family of distributions for which the linear model is said to be 'generalized'.
The parameters estimated during simple linear and multiple linear regression analyses are relatively straightforward to interpret (they simply represent the rates of change in the response variable attributable to each individual predictor variable) and can be used to construct an algebraic representation of the relationship between a response variable and one or more predictor variables. However, this is generally not the case for linear models containing factorial variables.
Linear models with factorial variables
Recall from above that linear models comprising of a single factor are expressed as an effects model: $$y_{ij} = \mu + \alpha_i + \varepsilon_{ij}$$ where $\alpha_i$ estimates the effect of each treatment group on the overall mean of groups ($\alpha_i=\mu_i-\mu$).
However, the effects model for a factor with $p$ groups, will have $p+1$ parameters (the overall mean $\mu$ plus the $p$ $\alpha$ parameters), and thus the linear effects model is considered to be `over-parameterized'. Given that $\alpha_i=\mu_i - \mu$, it is only possible to estimate $p-1$ orthogonal (independent) parameters. For example, once $\mu$ and $p-1$ of the effects parameters have been estimated, the final effects parameter is no longer `free to vary' and therefore cannot be independently estimated. Likewise, if the full linear model contains as many dummy variables as there are treatment groups, then it too is over-parameterized.
In order to obtain parameter estimates, the model must be reduced to a total of $p$ parameters. Over-parameterization can be resolved by one of two alternative parameterizations
- means parameterization - removing one of the parameters from the effects model (either the overall mean ($\mu$) or one of the treatment effects ($\alpha_i$) parameters - a procedure rarely used in a frequentist framework in biology). When it is the overall mean that is removed, then each of the regression parameters represent the mean of a group. $$y_i = \alpha_p+\varepsilon_i, \hspace{2cm}\text{where}~p= \text{number of levels of the factor}$$ $$\begin{pmatrix} 2\\3\\4\\6\\7\\8\\10\\11\\12 \end{pmatrix} = \begin{pmatrix} 1&0&0\\1&0&0\\1&0&0\\0&1&0\\0&1&0\\0&1&0\\0&0&1\\0&0&1\\0&0&1 \end{pmatrix} \times \begin{pmatrix} \alpha_1\\\alpha_2\\\alpha_3 \end{pmatrix} + \begin{pmatrix} \varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\varepsilon_4&\\\varepsilon_5\\\varepsilon_6\\\varepsilon_7&\\\varepsilon_8\\\varepsilon_9 \end{pmatrix} $$
- effects parameterization - generating a new set ($p-1$) of effects parameters ($\alpha^*_{q}$, where $q$ represents the set of orthogonal parameters from 2 to $p$) each of which represent a linear combination of groups rather than a single group effect. That is, each $\alpha^*$ can include varying contributions from any number of the groups and are not restricted to a single contrast of ($=\mu_i-\mu$). For example, one of the parameters might represent the difference in means between two groups or the difference in means between one group and the average of two other groups. $$y_i = \mu+\alpha_q+\varepsilon_i, \hspace{2cm}\text{where}~q= 2:p$$ In the effects parameterization, $\mu$ typically represents the mean of one of the groups (a reference group) and each of the $\alpha$ effects represent the difference between subsequent group means and the reference group. $$\begin{pmatrix} 2\\3\\4\\6\\7\\8\\10\\11\\12 \end{pmatrix} = \begin{pmatrix} 1&0&0\\1&0&0\\1&0&0\\1&1&0\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\1&0&1 \end{pmatrix} \times \begin{pmatrix} \alpha_1\\\alpha_2\\\alpha_3\\\alpha_4 \end{pmatrix} + \begin{pmatrix} \varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\varepsilon_4&\\\varepsilon_5\\\varepsilon_6\\\varepsilon_7&\\\varepsilon_8\\\varepsilon_9 \end{pmatrix} $$
The reduced number of effects parameters are defined through the use of a matrix of `contrast coefficients'. Note, the new set of effects parameters should incorporate the overall relational effects of each of the groups equally such that each group maintains an equal contribution to the overall model fit. The contrast coefficients are responsible for determining how the model is re-parameterized into an orthogonal model matrix.
A number of `pre-fabricated', contrast matrices exist (to yield commonly used model matrices), each of which estimate a different set of specific comparisons between treatment combinations.
To compare the common forms of model parameterization, lets create the above data within R.
#response Y <- c(2,3,4,6,7,8,10,11,12) #Factor A A <- gl(3,3,9,lab=c("G1","G2","G3")) #calculate the group means tapply(Y, A, mean)
G1 G2 G3 3 7 11
Means parameterization
Means parameterization literally estimates the group means. Whilst this would initially seem the most obvious approach, as it estimates the mean and standard error of each treatment group, it does not yield meaningful hypothesis tests.
| Parameter | Estimates | Null hypothesis |
|---|---|---|
| $\alpha^*_1$ | mean of group 1 ($\mu_1$) | H$_0$: $\mu=\mu_1=0$ |
| $\alpha^*_2$ | mean of group 2 ($\mu_2$) | H$_0$: $\mu=\mu_2=0$ |
| $\alpha^*_3$ | mean of group 3 ($\mu_3$) | H$_0$: $\mu=\mu_3=0$ |
| ... |
model.matrix(~-1+A)
AG1 AG2 AG3 1 1 0 0 2 1 0 0 3 1 0 0 4 0 1 0 5 0 1 0 6 0 1 0 7 0 0 1 8 0 0 1 9 0 0 1 attr(,"assign") [1] 1 1 1 attr(,"contrasts") attr(,"contrasts")$A [1] "contr.treatment"
summary(lm(Y~-1+A))
Call:
lm(formula = Y ~ -1 + A)
Residuals:
Min 1Q Median 3Q Max
-1 -1 0 1 1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
AG1 3.0000 0.5774 5.196 0.00202 **
AG2 7.0000 0.5774 12.124 1.91e-05 ***
AG3 11.0000 0.5774 19.053 1.35e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared: 0.989, Adjusted R-squared: 0.9834
F-statistic: 179 on 3 and 6 DF, p-value: 2.939e-06
Treatment contrasts
Treatment contrasts are contrasts in which each of the treatment groups means are compared to the mean of a `control' or reference group. This approach to over-parameterization is computationally identical to fitting $p-1$ dummy variables via multiple linear regression. However, due to the interpretation of the parameters (groups compared to a control) and the fact that treatment effects are not orthogonal to the intercept, the interpretation of treatment contrasts (and thus dummy regression) is really only meaningful for situations where there is clearly a single group (control) to which the other groups can be compared. For treatment contrasts, the intercept is replaced by $\alpha^*_{1}$ and thus the remaining $\alpha^*_{q}$ parameters are numbered starting at 2.
| Parameter | Estimates | Null hypothesis |
|---|---|---|
| $Intercept$ | mean of `control' group ($\mu_1$) | H$_0$: $\mu=\mu_1=0$ |
| $\alpha^*_2$ | mean of group 2 minus mean of `control' group ($\mu_2-\mu_1$) | H$_0$: $\alpha^*_2=\mu_2-\mu_1=0$ |
| $\alpha^*_3$ | mean of group 3 minus mean of `control' group ($\mu_3-\mu_1$) | H$_0$: $\alpha^*_3=\mu_3-\mu_1=0$ |
| ... |
contrasts(A) <-contr.treatment model.matrix(~A)
(Intercept) A2 A3 1 1 0 0 2 1 0 0 3 1 0 0 4 1 1 0 5 1 1 0 6 1 1 0 7 1 0 1 8 1 0 1 9 1 0 1 attr(,"assign") [1] 0 1 1 attr(,"contrasts") attr(,"contrasts")$A 2 3 G1 0 0 G2 1 0 G3 0 1
summary(lm(Y~A))
Call:
lm(formula = Y ~ A)
Residuals:
Min 1Q Median 3Q Max
-1 -1 0 1 1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0000 0.5774 5.196 0.00202 **
A2 4.0000 0.8165 4.899 0.00271 **
A3 8.0000 0.8165 9.798 6.51e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared: 0.9412, Adjusted R-squared: 0.9216
F-statistic: 48 on 2 and 6 DF, p-value: 0.0002035
Sum to zero contrasts
This technique constrains the sum of the unconstrained treatment effects ($\alpha$) to zero. In this model parameterization, the intercept estimates the average treatment effect and the remaining ($\alpha^*$) estimate the differences between each of the treatment means and the average treatment mean. Unlike treatment contrasts, these contrasts are genuinely orthogonal.
| Parameter | Estimates | Null hypothesis |
|---|---|---|
| $Intercept$ | mean of group means ($\mu_{q}/p$) | H$_0$: $\mu=\mu_{q}/p=0$ |
| $\alpha^*_2$ | mean of group 1 minus mean of group means ($\mu_1-(\mu_{q}/p)$) | H$_0$: $\alpha_1=\mu_1-(\mu_{q}/p)=0$ |
| $\alpha^*_3$ | mean of group 2 minus mean of group means ($\mu_2-(\mu_{q}/p)$) | H$_0$: $\alpha_2=\mu_2-(\mu_{q}/p)=0$ |
| ... |
contrasts(A) <-contr.sum model.matrix(~A)
(Intercept) A1 A2 1 1 1 0 2 1 1 0 3 1 1 0 4 1 0 1 5 1 0 1 6 1 0 1 7 1 -1 -1 8 1 -1 -1 9 1 -1 -1 attr(,"assign") [1] 0 1 1 attr(,"contrasts") attr(,"contrasts")$A [,1] [,2] G1 1 0 G2 0 1 G3 -1 -1
summary(lm(Y~A))
Call:
lm(formula = Y ~ A)
Residuals:
Min 1Q Median 3Q Max
-1 -1 0 1 1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.000e+00 3.333e-01 21.000 7.6e-07 ***
A1 -4.000e+00 4.714e-01 -8.485 0.000147 ***
A2 -2.093e-16 4.714e-01 0.000 1.000000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared: 0.9412, Adjusted R-squared: 0.9216
F-statistic: 48 on 2 and 6 DF, p-value: 0.0002035
Helmert contrasts
In Helmert contrasts, the intercept estimates the average treatment effect and the remaining ($\alpha^*_{q}$) estimate the differences between each of the treatment means and the mean of the group before it. In reality, parameter estimates from Helmert contrasts have little biological interpretability.
| Parameter | Estimates | Null hypothesis |
|---|---|---|
| $Intercept$ | mean of group means ($\mu_{q}/p$) | H$_0$: $\mu=\mu_{q}/p=0$ |
| $\alpha^*_2$ | mean of group 2 minus mean of (group means and mean of group1) ($\mu_2-(\mu_{q}/p + \mu_1)/2$) | H$_0$: $\alpha^*_1=\mu_2-(\mu_{q}/p+\mu_1)/2=0$ |
| $\alpha^*_3$ | mean of group 3 minus mean of (group means, mean of group1 and mean of group2) ($\mu_3-(\mu_{q}/p + \mu_1 + \mu_2)/3$) | H$_0$: $\alpha^*_2=\mu_3-(\mu_{q}/p+\mu_1+\mu_2)/3=0$ |
| ... |
contrasts(A) <-contr.helmert model.matrix(~A)
(Intercept) A1 A2 1 1 -1 -1 2 1 -1 -1 3 1 -1 -1 4 1 1 -1 5 1 1 -1 6 1 1 -1 7 1 0 2 8 1 0 2 9 1 0 2 attr(,"assign") [1] 0 1 1 attr(,"contrasts") attr(,"contrasts")$A [,1] [,2] G1 -1 -1 G2 1 -1 G3 0 2
summary(lm(Y~A))
Call:
lm(formula = Y ~ A)
Residuals:
Min 1Q Median 3Q Max
-1 -1 0 1 1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.0000 0.3333 21.000 7.6e-07 ***
A1 2.0000 0.4082 4.899 0.002714 **
A2 2.0000 0.2357 8.485 0.000147 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared: 0.9412, Adjusted R-squared: 0.9216
F-statistic: 48 on 2 and 6 DF, p-value: 0.0002035
Polynomial contrasts
Polynomial contrasts generate orthogonal polynomial trends (such as linear, quadratic and cubic). This is equivalent to fitting a multiple linear regression (or polynomial regression) with orthogonal parameters. $p-1$ order polynomials are defined. Polynomial contrasts are obviously only sensible for factors whose levels can be conceptualized as representing an ordered, continuum. Unless otherwise specified, the intervals between levels are assumed to be equally spaced. The first, second and third order polynomials respectively represent straight line (linear), curves with a single major change in direction (quadratic) and curves with two major changes in direction (cubic).
| Parameter | Estimates | Null hypothesis |
|---|---|---|
| $Intercept$ | y-intercept | H$_0$: $\beta^*_0=0$ |
| $\beta^*_1$ | partial slope for linear term | H$_0$: $\beta^*_1=0$ |
| $\beta^*_2$ | partial slope for quadratic term | H$_0$: $\beta^*_2=0$ |
| ... |
contrasts(A) <-contr.poly model.matrix(~A)
(Intercept) A.L A.Q
1 1 -7.071068e-01 0.4082483
2 1 -7.071068e-01 0.4082483
3 1 -7.071068e-01 0.4082483
4 1 -7.850462e-17 -0.8164966
5 1 -7.850462e-17 -0.8164966
6 1 -7.850462e-17 -0.8164966
7 1 7.071068e-01 0.4082483
8 1 7.071068e-01 0.4082483
9 1 7.071068e-01 0.4082483
attr(,"assign")
[1] 0 1 1
attr(,"contrasts")
attr(,"contrasts")$A
.L .Q
G1 -7.071068e-01 0.4082483
G2 -7.850462e-17 -0.8164966
G3 7.071068e-01 0.4082483
summary(lm(Y~A))
Call:
lm(formula = Y ~ A)
Residuals:
Min 1Q Median 3Q Max
-1 -1 0 1 1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.0000 0.3333 21.000 7.60e-07 ***
A.L 5.6569 0.5774 9.798 6.51e-05 ***
A.Q 0.0000 0.5774 0.000 1
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared: 0.9412, Adjusted R-squared: 0.9216
F-statistic: 48 on 2 and 6 DF, p-value: 0.0002035
User defined contrasts
In addition to the `prefabricated' sets of comparisons illustrated above, it is possible to define other contrast combinations that are specifically suited to a particular experimental design and set of research questions. Contrasts are defined by constructing a contrast matrix according to the following rules:
- groups to be included and excluded in a specific contrasts (comparison) are represented by non-zero and zero coefficients respectively
- groups to be apposed (contrasted) to one another should have apposing signs
- the number of contrasts must not exceed $p-1$, where $p$ is the number of groups. Actually, it must equal $p-1$ exactly. However, it is usually sufficient to define less than $p-1$ contrasts and let R generate the remaining contrasts.
- within a given contrast, the sum of positive coefficients (and negative coefficients) should sum to 1 to ensure that the resulting estimates can be sensibly interpreted.
- all the contrasts must be orthogonal (independent of one another)
# define potential contrast matrix for comparing group G1 with the average of groups G2 and G3 library(gmodels) contrasts(A) <- make.contrasts(rbind(c(1, -0.5, -0.5))) contrasts(A)
C1 C2 G1 0.6666667 5.551115e-17 G2 -0.3333333 -7.071068e-01 G3 -0.3333333 7.071068e-01
model.matrix(~A)
(Intercept) AC1 AC2
1 1 0.6666667 5.551115e-17
2 1 0.6666667 5.551115e-17
3 1 0.6666667 5.551115e-17
4 1 -0.3333333 -7.071068e-01
5 1 -0.3333333 -7.071068e-01
6 1 -0.3333333 -7.071068e-01
7 1 -0.3333333 7.071068e-01
8 1 -0.3333333 7.071068e-01
9 1 -0.3333333 7.071068e-01
attr(,"assign")
[1] 0 1 1
attr(,"contrasts")
attr(,"contrasts")$A
C1 C2
G1 0.6666667 5.551115e-17
G2 -0.3333333 -7.071068e-01
G3 -0.3333333 7.071068e-01
summary(lm(Y~A))
Call:
lm(formula = Y ~ A)
Residuals:
Min 1Q Median 3Q Max
-1 -1 0 1 1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.0000 0.3333 21.000 7.6e-07 ***
AC1 -6.0000 0.7071 -8.485 0.000147 ***
AC2 2.8284 0.5774 4.899 0.002714 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1 on 6 degrees of freedom
Multiple R-squared: 0.9412, Adjusted R-squared: 0.9216
F-statistic: 48 on 2 and 6 DF, p-value: 0.0002035
Alternatively, it is possible to examine a set of planned contrasts after fitting a model. This can be done with the help of the glht() function in the multcomp package.
contrasts(A) <- contr.treatment data.lm <- lm(Y~A) library(multcomp) summary(glht(data.lm, linfct=cbind(0, rbind(c(1,-0.5,-0.5)) %*% contr.treatment(3))))
Simultaneous Tests for General Linear Hypotheses
Fit: lm(formula = Y ~ A)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
1 == 0 -6.0000 0.7071 -8.485 0.000147 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)
More about what's under the hood
By default, R employs treatment contrasts for unordered factors (factors that have not specifically defined as `ordered' - the order of groups in an ordered factor is usually important - for example when examining polynomial trends across groups ) and orthogonal polynomial contrasts for ordered factors, although this behavior can be altered to an alternative (such as contr.sum for unordered factors) using the options(contrasts=c("contr.sum", "contr.poly")) function. Note that the default behaviour of S-PLUS is to employ sum to zero contrasts for unordered factors.
Note that while the estimates and interpretations of individual model parameters differ between the alternative parametersization, in all but the $\mu=0$ (means parameterization or 'set-to-zero' contrasts) case, the overall effects model is identical ($y_{qj}=\mu+\alpha^*_{q}+\varepsilon_{qj}$). Hence, the overall null hypothesis tested from the effects model (H$_0$: $\alpha^*_1=\alpha^*_2=...=0$) is the same irrespective of the contrasts chosen.
When the model contains more than one factor, a separate term is assigned for each factor and possibly the interactions between factors (e.g. $\alpha_i + \beta_j + \alpha\beta_{ij}$). Alternatively, statistical models containing factors can be expressed as cell means models (means parameterization) in which the overall mean and treatment effects ($\mu + \alpha_{i}$) are replaced by the treatment (cell) means ($\mu_i$). In the cell means model, there are as many cell means as there are unique treatment levels. These differences are thus summarized: \begin{align*} Linear~model~y_{ij} &= \mu + \beta_1(dummy_1)_{ij} + \beta_2(dummy_2)_{ij} + .... + \varepsilon_{ij}\\ Linear~effects~model~y_{ij} &= \mu + \alpha_{i} + \varepsilon_{ij}\\ Orthogonal~linear~effects~model~y_{i^*j} &= \mu + \alpha^*_{i^*} + \varepsilon_{i^*j}\\ Cell~means~model~y_{ij} &= \mu_i + \varepsilon_{ij}\\ \end{align*}
For simple model fitting the choice of model type makes no difference, however for complex factorial models in which entire treatment levels (cells) are missing, full effects models cannot be fitted and therefore cell means models must be used.
Linear model hypothesis testing
Frequentistic inference and hypothesis testing is usually concerned with evaluating whether a population parameter is (or set of parameters are) equal to zero, as this signifies no `relationship' or `effect'. Evidence against this null outcome thereby provides evidence for the opposite situation - an effect.
Null hypotheses about individual parameters
In a linear model, there is a null hypothesis associated with each of the individual model parameters (typically that the parameter is equal to zero), although not all the testable null hypotheses are necessarily biologically meaningful. Consider again the simple linear regression model: $$y_i=\beta_0+\beta_1x_i+\varepsilon_i$$ This linear model includes two parameters ($\beta_0$ and $\beta_1$), and thus there are two individual testable null hypotheses:
- that the population y-intercept is equal to zero (H$_0$: $\beta_0=0$) and
- the slope is equal to zero (H$_0$: $\beta_1=0$).
Null hypotheses about individual model parameters are usually tested using a \textit{t}-test (see Tutorial 6.2a), or equivalently via a single factor ANOVA (see Tutorial 7.4a) with a single degree of freedom. The latter approach is often employed when user-defined contrasts are involved as it enables the results to be expressed in the context of the overall linear model.
Null hypotheses about the fit of the overall model
Recall that in hypothesis testing, a null hypothesis ($H_0$) is formulated to represent all possibilities except the hypothesized prediction and that disproving the null hypothesis provides evidence that some alternative hypothesis ($H_A$) is true. Consequently, there are typically at least two models fitted:
- the reduced model, in which the parameter of interest (and its associated predictor variable) is absent (or equivalently set to zero) represents the model predicted by null hypothesis.
- the full model represents the alternative hypothesis and includes the term of interest.
The degree to which a model 'fits' the observed data is determined by the amount of variation that the model fails to explain, and is measured as the sum of the squared differences (termed $SS$ or sums-of-squares) between the observed values of the response variable and the values predicted by the model. A model that fits the observed data perfectly will have a \textit{SS} of 0.
The reduced model measures the amount of variation left unexplained by the statistical model when the contribution of the parameter and predictor variable (term) of interest is removed ($SS_{Total}$). The full model measures the amount of variation left unexplained by the statistical model when the contribution of the term is included ($SS_{Residual}$).
The difference between the reduced and full models ($SS_{Model}$) is the amount of explained variation attributed to the term of interest. When the null hypothesis is true, the term of interest should not explain any of the variability in the observed data and thus the full model will not fit the observed data any better than the reduced model. That is, the proposed model would not be expected to explain any more of the total variation than it leaves unexplained. If however, the full model fits the data 'significantly' better (unexplained variability is substantially less in the full model compared to the reduced model) than the reduced model, there is evidence to reject the null hypothesis in favour of the alternative hypothesis.
Hypothesis testing formally evaluates this proposition by comparing the ratio of explained and unexplained variation to a probability distribution representing all possible ratios theoretically obtainable when the null hypothesis is true. The total variability in the observed data ($SS_{Residual}$ - reduced model) is partitioned into at least two sources:
- the variation that is explained by the model ($SS_{Model}$)
$SS_{Model} = SS_{Total}~(reduced~model) - SS_{Residual}~(full~model)$ - the variation that is unexplained by the model ($SS_{Residual}$)
$SS_{Residual}~(full~model)$
The number of degrees of freedom (d.f.) associated with estimates of each source of variation reflect the number of observations involved in the estimate minus the number of other parameters that must have been estimated previously. Just like $SS$, $df$ are additive and therefore: $$df_{Model} = df_{Total}~(reduced~model) - df_{Residual}~(full~model)$$
Each of the sources of variation are based on a different number of contributing observations. Therefore more comparable, standardized versions are generated by dividing by the appropriate number of (degrees of freedom). These averaged measures of variation (known as mean squares or $MS$) are thus conservative mean measures of variation and importantly, they have known probability distributions (unlike the SS estimates).
The partitioned sources of variation are tabulated in the form of an analysis of variance (ANOVA) table (see Table below), which also includes the ratio (F-ratio) of $MS_{Model}$ to $MS_{Residual}$. When the null hypothesis is true $MS_{Model}$ and $MS_{Residual}$ are expected to be the same, and thus their ratio (F-ratio) should be approximately 1. An F-ratio based on observed data is thus compared to an appropriate F-distribution (theoretical distribution of all possible F-ratios for the set of degrees of freedom) when the null hypothesis is true. If the probability of obtaining such an F-ratio (or one more extreme) is less than a critical value, the null hypothesis is rejected.
In the following analysis of variance (ANOVA) table for a simple linear model, $n$ is the number of observations, $f_p$ is the number of parameters in the full model and $r_p$ is the number of parameters in the reduced model.
| Source of variation | SS | df | MS | F-ratio |
|---|---|---|---|---|
| Model | $SS_{Model}$ | $f_p-1$ | $\frac{SS_{Model}}{df_{Model}}$ | $\frac{MS_{Model}}{MS_{Residual}}$ |
| Residual | $SS_{Residual}$ | $n-f_p$ | $\frac{SS_{Residual}}{df_{Residual}}$ | |
| Total | $SS_{Total}$ | $n-r_p$ | $\frac{SS_{Total}}{df_{Total}}$ |
When there are multiple predictor variables, in addition to assessing the fit of the overall model, we usually want to determine the effect of individual factors. This is done by comparing the fit of models with and without the specific term(s) associated with that variable.
Comments about the importance of understanding the structure and parameterization of linear models
An understanding of how to formulate the correct statistical model from a design and set of null hypotheses is crucial to ensure that the correct R syntax (and thus analysis) is employed. This is particularly important for more complex designs which incorporate multiple error strata (such as partly nested ANOVA). The following table briefly illustrates the ways in which statistical models are represented in R. Moreover, in each of the remaining tutorials, the statistical models as well as the appropriate R model formulae for each major form of modeling will be highlighted and demonstrated, thereby providing greater details about use of R in statistical modeling.
| Linear model | R model formula | Description |
|---|---|---|
| $y_i=\beta_0 + \beta_1x_i$ | y∼1+x y∼x | Simple linear regression model of y on x with intercept term included |
| $y_i=\beta_1x_i$ | y∼0+x y∼-1+x y∼x-1 | Simple linear regression model of y on x with intercept term excluded |
| $y_i=\beta_0$ | y∼1 y∼1-x | Simple linear regression model of y against the intercept term - basically just calculates the mean of y |
| $y_i=\beta_0 + \beta_1x_{i1} + \beta_2x_{i2}$ | y∼x1+x2 | Multiple linear regression model of y on x1 and x2 with the intercept term included implicitly |
| $y_i=\beta_0 + \beta_1x_{i1} + \beta_2x_{i1}^2$ | y∼x+I(x^2) y∼poly(x,2) | Second order polynomial regression of y on x This second form uses orthogonal polynomials. |
| $y_{ij}=\mu+\alpha_i$ | y∼A | Analysis of variance of y against a single factor A |
| $y_{ijk}=\mu+\alpha_i + \beta_j + \alpha\beta_{ij}$ | y∼A+B+A:B y∼A*B | Multiplicative fully factorial analysis of variance of y against A and B |
| $y_{ijk}=\mu+\alpha_i + \beta_j$ | y∼A+B y∼A*B-A:B | Additive, fully factorial analysis of variance of y against A and B without the interaction term |
| $y_{ijk}=\mu+\alpha_i + \beta_{j(i)}$ | y∼B %in% A y∼A/B | Nested analysis of variance of y against A and B nested within A |
| $y_{ij}=\mu+\alpha_i+\beta(x_{ij}-\bar{x})$ | y∼A*x y∼A/x | Analysis of covariance of y on x at each level of A |
| $y_{ijkl}=\mu+\alpha_i+\beta_{j(i)}+\gamma_k + \alpha\gamma_{ik} + \beta\gamma_{j(i)k}$ | y∼A+Error(B)+C+A:C+B:C | Partly nested ANOVA of y against a single between block factor (A), a single within block factor (C) and a single random blocking factor (B) |
Defining Bayesian models reflects the underlying statistical models and error distributions even more closely and thus it is absolutely imperative that you can understand and formulate the appropriate statistical model prior to attempting to impliment a programatic instance of the model definition. For the remaining tutorials involving Bayesian analyses, the statstical models will be always be highlighted prior to defining the JAGS model so as to further emphasise the link between the theoretical and practical statistical models.
