Tutorial 9.6b - Factorial ANOVA (Bayesian)
14 Jan 2014
Overview
Factorial designs are an extension of single factor ANOVA designs in which additional factors are added such that each level of one factor is applied to all levels of the other factor(s) and these combinations are replicated.
For example, we might design an experiment in which the effects of temperature (high vs low) and fertilizer (added vs not added) on the growth rate of seedlings are investigated by growing seedlings under the different temperature and fertilizer combinations.
The following diagram depicts a very simple factorial design in which there are two factors (Shape and Color) each with two levels (Shape: square and circle; Color: blue and white) and each combination has 3 replicates.
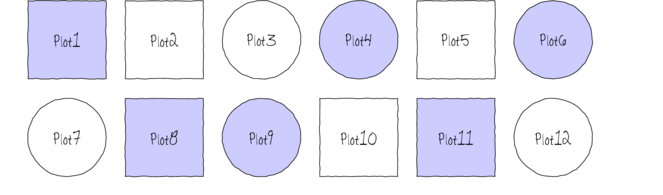
In addition to investigating the impacts of the main factors, factorial designs allow us to investigate whether the effects of one factor are consistent across levels of another factor. For example, is the effect of temperature on growth rate the same for both fertilized and unfertilized seedlings and similarly, does the impact of fertilizer treatment depend on the temperature under which the seedlings are grown?
Arguably, these interactions give more sophisticated insights into the dynamics of the system we are investigating. Hence, we could add additional main effects, such as soil pH, amount of water etc along with all the two way (temp:fert, temp:pH, temp:water, etc), three-way (temp:fert:pH, temp:pH:water), four-way etc interactions in order to explore how these various factors interact with one another to effect the response.
However, the more interactions, the more complex the model becomes to specify, compute and interpret - not to mention the rate at which the number of required observations increases.
To appreciate the interpretation of interactions, consider the following figure that depicts fictitious two factor (temperature and fertilizer) designs.
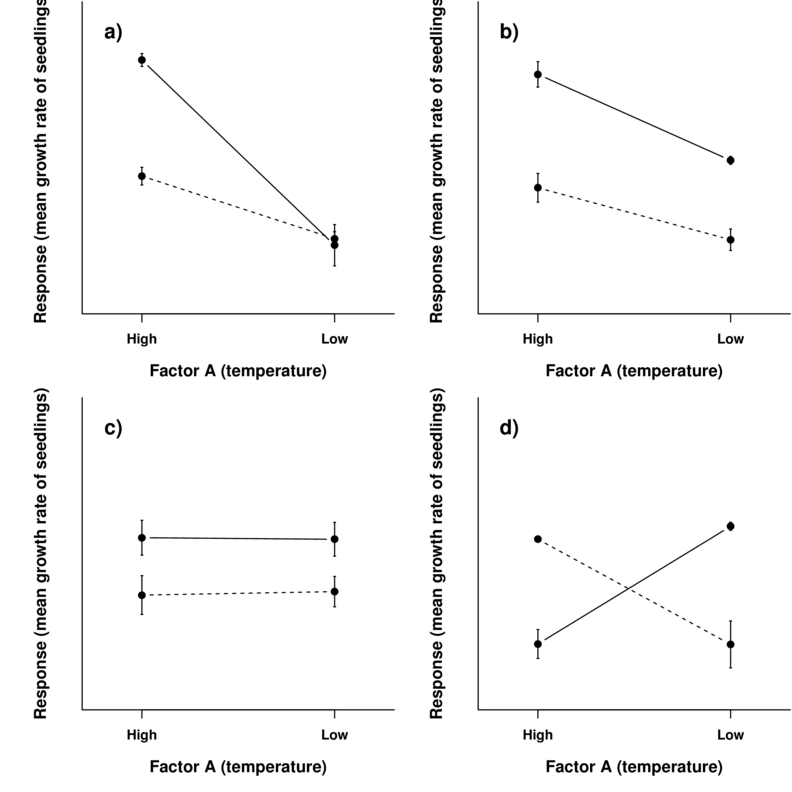
It is clear from the top-right figure that whether or not there is an observed effect of adding fertilizer or not depends on whether we are focused on seedlings growth under high or low temperatures. Fertilizer is only important for seedlings grown under high temperatures. In this case, it is not possible to simply state that there is an effect of fertilizer as it depends on the level of temperature. Similarly, the magnitude of the effect of temperature depends on whether fertilizer has been added or not.
Such interactions are represented by plots in which lines either intersect or converge. The top-right and bottom-left figures both depict parallel lines which are indicative of no interaction. That is, the effects of temperature are similar for both fertilizer added and controls and vice verse. Whilst the former displays an effect of both fertilizer and temperature, the latter only fertilizer is important.
Finally, the bottom-right figure represents a strong interaction that would mask the main effects of temperature and fertilizer (since the nature of the effect of temperature is very different for the different fertilizer treatments and visa verse).
In a frequentist framework, factorial designs can consist:
- entirely of crossed fixed factors (Model I ANOVA - most common) in which conclusions are restricted to the specific combinations of levels selected for the experiment,
- entirely of crossed random factors (Model II ANOVA) or
- a mixture of crossed fixed and random factors (Model III ANOVA).
The tutorial on frequentist factorial ANOVA described procedures used to further investigate models in the presence of significant interactions as well as the complications that arise with linear models fitted to unbalanced designs. Again, these issues largely evaporate in a Bayesian framework. Consequently, we will not really dwell on these complications in this tutorial. At most, we will model some unbalanced data, yet it should be noted that we will not need to make any special adjustments in order to do so.
Linear model
The generic linear model is presented here purely for revisory purposes. If, it is unfamiliar to you or you are unsure about what parameters are to be estimated and tested, you are strongly advised to review the the tutorial on frequentist factorial ANOVA
The linear models for two and three factor design are: $$y_{ijk}=\mu+\alpha_i + \beta_{j} + (\alpha\beta)_{ij} + \varepsilon_{ijk}$$ $$y_{ijkl}=\mu+\alpha_i + \beta_{j} + \gamma_{k} + (\alpha\beta)_{ij} + (\alpha\gamma)_{ik} + (\beta\gamma)_{jk} + (\alpha\beta\gamma)_{ijk} + \varepsilon_{ijkl}$$ where $\mu$ is the overall mean, $\alpha$ is the effect of Factor A, $\beta$ is the effect of Factor B, $\gamma$ is the effect of Factor C and $\varepsilon$ is the random unexplained or residual component.
Scenario and Data
Imagine we has designed an experiment in which we had measured the response ($y$) under a combination of two different potential influences (Factor A: levels $a1$ and $a2$; and Factor B: levels $b1$, $b2$ and $b3$), each combination replicated 10 times ($n=10$). As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the sample size per treatment=10
- factor A with 2 levels
- factor B with 3 levels
- the 6 effects parameters are 40, 15, 5, 0, -15,10 ($\mu_{a1b1}=40$, $\mu_{a2b1}=40+15=55$, $\mu_{a1b2}=40+5=45$, $\mu_{a1b3}=40+0=40$, $\mu_{a2b2}=40+15+5-15=45$ and $\mu_{a2b3}=40+15+0+10=65$)
- the data are drawn from normal distributions with a mean of 0 and standard deviation of 3 ($\sigma^2=9$)
> set.seed(1) > nA <- 2 #number of levels of A > nB <- 3 #number of levels of B > nsample <- 10 #number of reps in each > A <- gl(nA, 1, nA, lab = paste("a", 1:nA, sep = "")) > B <- gl(nB, 1, nB, lab = paste("b", 1:nB, sep = "")) > data <- expand.grid(A = A, B = B, n = 1:nsample) > X <- model.matrix(~A * B, data = data) > eff <- c(40, 15, 5, 0, -15, 10) > sigma <- 3 #residual standard deviation > n <- nrow(data) > eps <- rnorm(n, 0, sigma) #residuals > data$y <- as.numeric(X %*% eff + eps) > head(data) #print out the first six rows of the data set
A B n y 1 a1 b1 1 38.12 2 a2 b1 1 55.55 3 a1 b2 1 42.49 4 a2 b2 1 49.79 5 a1 b3 1 40.99 6 a2 b3 1 62.54
> with(data, interaction.plot(A, B, y))
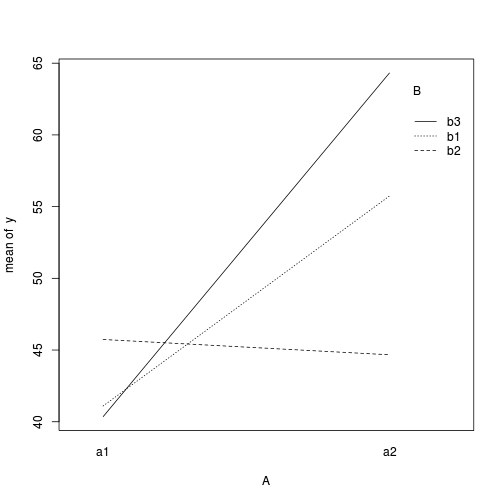
> > ## ALTERNATIVELY, we could supply the population means and get the effect parameters from these. To > ## correspond to the model matrix, enter the population means in the order of: a1b1, a2b1, a1b1, > ## a2b2,a1b3,a2b3 > pop.means <- as.matrix(c(40, 55, 45, 45, 40, 65), byrow = F) > ## Generate a minimum model matrix for the effects > XX <- model.matrix(~A * B, expand.grid(A = factor(1:2), B = factor(1:3))) > ## Use the solve() function to solve what are effectively simultaneous equations > (eff <- as.vector(solve(XX, pop.means)))
[1] 40 15 5 0 -15 10
> data$y <- as.numeric(X %*% eff + eps)
With these sort of data, we are primarily interested in investigating whether there is a relationship between the continuous response variable and the treatment type. Does treatment type effect the response.
Assumptions
- All of the observations are independent - this must be addressed at the design and collection stages. Importantly, to be considered independent replicates, the replicates must be made at the same scale at which the treatment is applied. For example, if the experiment involves subjecting organisms housed in tanks to different water temperatures, then the unit of replication is the individual tanks not the individual organisms in the tanks. The individuals in a tank are strictly not independent with respect to the treatment.
- The response variable (and thus the residuals) should be normally distributed for each sampled populations (combination of factors). Boxplots of each treatment combination are useful for diagnosing major issues with normality.
- The response variable should be equally varied (variance should not be related to mean as these are supposed to be estimated separately) for each combination of treatments. Again, boxplots are useful.
Exploratory data analysis
Normality and Homogeneity of variance
> boxplot(y ~ A * B, data)
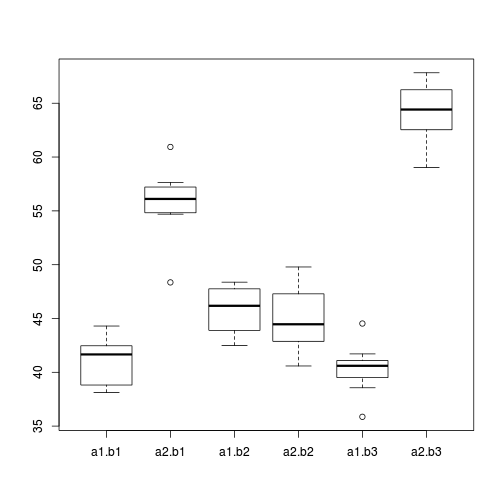
Conclusions:
- there is no evidence that the response variable is consistently non-normal across all populations - each boxplot is approximately symmetrical
- there is no evidence that variance (as estimated by the height of the boxplots) differs between the five populations. . More importantly, there is no evidence of a relationship between mean and variance - the height of boxplots does not increase with increasing position along the y-axis. Hence it there is no evidence of non-homogeneity
- transform the scale of the response variables (to address normality etc). Note transformations should be applied to the entire response variable (not just those populations that are skewed).
Model fitting or statistical analysis
It is possible to model in all sorts of specific comparisons into the JAGS or STAN model statement (as we did for single factor ANOVA). Likewise, it is possible to define specific main effects type tests within the model statement. However, we will just define the minimum required model and perform all other posterior derivatives from the MCMC samples using R. This way, the techniques can be applied no mater which of the Bayesian modelling routines (JAGS, STAN, MCMCpack etc) were used.
JAGS
Effects model
$$y_{ij}\sim \mathcal{N}(\beta_i\times \mathbf{X}_i, \sigma^2)\\ \mathbf{X}_i = \mu+\alpha_i + \beta_{j} + (\alpha\beta)_{ij}\\ \mu\sim \mathcal{N}(0, 1.0E-6)\\ \beta_i\sim \mathcal{N}(0, 1.0E-6)\\ \sigma^2\sim \mathcal{U}(0,100) $$Bayesian factorial models can be parameterized as either as effects models or as cell means models. Furthermore, the models can be defined either in terms of a fully specified linear predictor (mirroring the right-hand side of the linear model), or as a model matrix. Adopting the model matrix notation dramatically simplifies the model specification (particularly if there are a few levels of each factor and/or more than two factors. Not only does this allow a more compact and generic model statement, as a result, it also makes model specification less error prone.
> modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mean[i],tau) mean[i] <- inprod(beta[],X[i,]) } #Priors and derivatives for (i in 1:p) { beta[i] ~ dnorm(0, 1.0E-6) #prior } sigma ~ dgamma(0.001, 0.001) tau <- 1 / (sigma * sigma) } " > writeLines(modelString,con="../downloads/BUGSscripts/tut9.6bS6.1.txt")
Actually, you might have noticed that this is the same model specification that was used for the single factor ANOVA via the model matrix. That is the point. The one model specification accommodates a huge range of linear models.
In creating a data list to pass to this JAGS model, we need to define a model matrix that reflects our intended linear model. This can be achieved simply via the model.matrix() function.
> X <- model.matrix(~A*B, data) > data.list <- with(data, + list(y=y, + X=X, + n=nrow(data), + p=ncol(X) + ) + ) > > params <- c("beta","sigma") > adaptSteps = 1000 > burnInSteps = 2000 > nChains = 3 > numSavedSteps = 50000 > thinSteps = 10 > nIter = ceiling((numSavedSteps * thinSteps)/nChains)
> library(R2jags)
jags.effects.simple.time <- system.time( data.r2jags <- jags(data=data.list, inits=NULL, parameters.to.save=params, model.file="../downloads/BUGSscripts/tut9.6bS6.1.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps ) )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 502 Initializing model
print(data.r2jags)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.6bS6.1.txt", fit using jags,
3 chains, each with 166667 iterations (first 2000 discarded), n.thin = 10
n.sims = 49401 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 41.098 0.837 39.450 40.538 41.090 41.654 42.758 1.001 36000
beta[2] 14.649 1.184 12.330 13.859 14.652 15.435 16.989 1.001 49000
beta[3] 4.639 1.184 2.298 3.849 4.640 5.431 6.969 1.001 49000
beta[4] -0.753 1.188 -3.094 -1.545 -0.753 0.043 1.589 1.001 30000
beta[5] -15.714 1.672 -19.024 -16.807 -15.718 -14.595 -12.448 1.001 49000
beta[6] 9.335 1.673 6.045 8.225 9.338 10.450 12.614 1.001 49000
sigma 2.636 0.260 2.185 2.453 2.617 2.796 3.207 1.001 49000
deviance 286.016 3.984 280.339 283.105 285.318 288.177 295.700 1.001 49000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 7.9 and DIC = 294.0
DIC is an estimate of expected predictive error (lower deviance is better).
data.mcmc.list <- as.mcmc(data.r2jags) Data.mcmc.list <- data.mcmc.list
Rstan
Model matrix
> rstanString=" data { int<lower=0> n; int<lower=0> p; vector[n] y; matrix [n,p] X; } parameters { vector[p] beta; real<lower=0> sigma; } model { vector[n] mu; #Priors beta ~ normal(0.01, 100000); sigma~ uniform(0,100); #Likelihood mu <- X*beta; y ~ normal(mu, sigma); } " > X <- model.matrix(~A*B,data) > data.list <- with(data, list(y = y, X = X, n = nrow(data), p = ncol(X))) > > nChains = 3 > burnInSteps = 3000 > thinSteps = 10 > numSavedSteps = 15000 #across all chains > nIter = ceiling(burnInSteps+(numSavedSteps * thinSteps)/nChains) > > library(rstan) > rstan.simple.time <- system.time( + data.rstan <- stan(data=data.list, + model_code=rstanString, + chains=nChains, + iter=nIter, + warmup=burnInSteps, + thin=thinSteps, + save_dso=TRUE + ) + )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW.
COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW.
SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1).
Iteration: 1 / 53000 [ 0%] (Warmup)
Iteration: 5300 / 53000 [ 10%] (Sampling)
Iteration: 10600 / 53000 [ 20%] (Sampling)
Iteration: 15900 / 53000 [ 30%] (Sampling)
Iteration: 21200 / 53000 [ 40%] (Sampling)
Iteration: 26500 / 53000 [ 50%] (Sampling)
Iteration: 31800 / 53000 [ 60%] (Sampling)
Iteration: 37100 / 53000 [ 70%] (Sampling)
Iteration: 42400 / 53000 [ 80%] (Sampling)
Iteration: 47700 / 53000 [ 90%] (Sampling)
Iteration: 53000 / 53000 [100%] (Sampling)
Elapsed Time: 0.28 seconds (Warm-up)
5.04 seconds (Sampling)
5.32 seconds (Total)
SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2).
Iteration: 1 / 53000 [ 0%] (Warmup)
Iteration: 5300 / 53000 [ 10%] (Sampling)
Iteration: 10600 / 53000 [ 20%] (Sampling)
Iteration: 15900 / 53000 [ 30%] (Sampling)
Iteration: 21200 / 53000 [ 40%] (Sampling)
Iteration: 26500 / 53000 [ 50%] (Sampling)
Iteration: 31800 / 53000 [ 60%] (Sampling)
Iteration: 37100 / 53000 [ 70%] (Sampling)
Iteration: 42400 / 53000 [ 80%] (Sampling)
Iteration: 47700 / 53000 [ 90%] (Sampling)
Iteration: 53000 / 53000 [100%] (Sampling)
Elapsed Time: 0.3 seconds (Warm-up)
5.42 seconds (Sampling)
5.72 seconds (Total)
SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3).
Iteration: 1 / 53000 [ 0%] (Warmup)
Iteration: 5300 / 53000 [ 10%] (Sampling)
Iteration: 10600 / 53000 [ 20%] (Sampling)
Iteration: 15900 / 53000 [ 30%] (Sampling)
Iteration: 21200 / 53000 [ 40%] (Sampling)
Iteration: 26500 / 53000 [ 50%] (Sampling)
Iteration: 31800 / 53000 [ 60%] (Sampling)
Iteration: 37100 / 53000 [ 70%] (Sampling)
Iteration: 42400 / 53000 [ 80%] (Sampling)
Iteration: 47700 / 53000 [ 90%] (Sampling)
Iteration: 53000 / 53000 [100%] (Sampling)
Elapsed Time: 0.27 seconds (Warm-up)
5.22 seconds (Sampling)
5.49 seconds (Total)
> print(data.rstan)
Inference for Stan model: rstanString.
3 chains, each with iter=53000; warmup=3000; thin=10;
post-warmup draws per chain=5000, total post-warmup draws=15000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta[1] 41.1 0 0.8 39.4 40.5 41.1 41.7 42.8 14709 1
beta[2] 14.7 0 1.2 12.3 13.8 14.6 15.5 17.0 14783 1
beta[3] 4.6 0 1.2 2.3 3.8 4.6 5.4 7.1 14579 1
beta[4] -0.7 0 1.2 -3.1 -1.5 -0.8 0.0 1.6 14910 1
beta[5] -15.7 0 1.7 -19.1 -16.8 -15.7 -14.6 -12.5 14678 1
beta[6] 9.3 0 1.7 6.1 8.2 9.3 10.5 12.6 14504 1
sigma 2.7 0 0.3 2.2 2.5 2.6 2.8 3.2 13829 1
lp__ -86.9 0 2.0 -91.7 -88.0 -86.6 -85.5 -84.1 15000 1
Samples were drawn using NUTS(diag_e) at Tue Feb 25 11:25:41 2014.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
> data.rstan.df <-as.data.frame(extract(data.rstan)) > head(data.rstan.df)
beta.1 beta.2 beta.3 beta.4 beta.5 beta.6 sigma lp__ 1 39.75 16.40 5.971 1.4991 -17.75 6.653 2.424 -85.73 2 39.74 14.05 6.798 1.6368 -16.85 8.913 2.649 -89.32 3 41.14 15.08 3.830 -0.9698 -16.53 9.511 2.477 -85.15 4 40.48 14.11 5.297 0.5224 -14.56 10.878 2.355 -88.23 5 40.12 15.32 5.918 0.3923 -17.59 10.278 2.557 -87.22 6 40.69 12.81 5.234 -1.2517 -14.62 13.137 2.549 -89.05
> > data.mcmc<-rstan:::as.mcmc.list.stanfit(data.rstan) > > > plyr:::adply(as.matrix(data.rstan.df),2,MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 beta.1 41.0955 37.51459 40.535 41.0955 41.6528 44.401 39.407 42.761 40.270 41.9263 2 beta.2 14.6357 10.10496 13.848 14.6357 15.4512 19.707 12.395 17.072 13.409 15.7779 3 beta.3 4.6413 0.04425 3.843 4.6413 5.4344 9.675 2.308 7.038 3.461 5.8125 4 beta.4 -0.7649 -6.85967 -1.538 -0.7649 0.0419 4.021 -3.168 1.519 -1.986 0.3503 5 beta.5 -15.7054 -22.86702 -16.819 -15.7054 -14.5661 -9.244 -19.014 -12.430 -17.337 -13.9972 6 beta.6 9.3374 2.84353 8.208 9.3374 10.4894 16.531 6.049 12.620 7.746 11.0858 7 sigma 2.6423 1.87165 2.477 2.6423 2.8290 4.157 2.177 3.191 2.372 2.8800 8 lp__ -86.6107 -99.28779 -88.015 -86.6107 -85.4866 -83.393 -90.856 -83.833 -87.947 -84.4797
> > comparisonTab <- cbind(comparisonTab,'Stan'=comTab(data.mcmc,cols="beta|sigma",lag=10,rstan.simple.time))
MCMCregress (MCMCpack)
> library(MCMCpack) > MCMCpack.additive.time <- system.time({ + data.MCMCregress.1 <- MCMCregress(y~A*B, data=data, burnin=3000, thin=10, mcmc=50000, seed=1234) + data.MCMCregress.2 <- MCMCregress(y~A*B, data=data, burnin=3000, thin=10, mcmc=50000, seed=5678) + data.MCMCregress.3 <- MCMCregress(y~A*B, data=data, burnin=3000, thin=10, mcmc=50000, seed=910111) + }) > > data.mcmc.list <- as.mcmc.list(list(data.MCMCregress.1,data.MCMCregress.2,data.MCMCregress.3)) > summary(data.mcmc.list)
Iterations = 3001:52991
Thinning interval = 10
Number of chains = 3
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
(Intercept) 41.106 0.835 0.00682 0.00669
Aa2 14.652 1.185 0.00967 0.00986
Bb2 4.634 1.187 0.00969 0.00962
Bb3 -0.762 1.190 0.00972 0.00964
Aa2:Bb2 -15.731 1.679 0.01371 0.01376
Aa2:Bb3 9.337 1.676 0.01369 0.01389
sigma2 7.013 1.409 0.01151 0.01130
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
(Intercept) 39.46 40.55 41.104 41.6671 42.76
Aa2 12.33 13.86 14.654 15.4412 16.99
Bb2 2.28 3.86 4.632 5.4232 6.96
Bb3 -3.09 -1.56 -0.773 0.0303 1.58
Aa2:Bb2 -19.05 -16.84 -15.731 -14.6393 -12.38
Aa2:Bb3 6.02 8.24 9.337 10.4622 12.60
sigma2 4.79 6.01 6.825 7.8067 10.28
> > nIter=150000 > thinSteps=10 > comparisonTab <- cbind(comparisonTab,'MCMCregress'=comTab(data.mcmc.list,cols="Intercept|A|B|sigma",lag=10,MCMCpack.additive.time)) >
MCMCglmm
> library(MCMCglmm) > MCMCglmm.time <- system.time({ + data.MCMCglmm.1 <- MCMCglmm(y~A*B, data=data, burnin=3000, thin=10, nitt=50000, verbose=FALSE) + data.MCMCglmm.2 <- MCMCglmm(y~A*B, data=data, burnin=3000, thin=10, nitt=50000, verbose=FALSE) + data.MCMCglmm.3 <- MCMCglmm(y~A*B, data=data, burnin=3000, thin=10, nitt=50000, verbose=FALSE) + }) > > data.mcmc.list<-mcmc.list( + as.mcmc(cbind(data.MCMCglmm.1$Sol,data.MCMCglmm.1$VCV)), + as.mcmc(cbind(data.MCMCglmm.2$Sol,data.MCMCglmm.2$VCV)), + as.mcmc(cbind(data.MCMCglmm.3$Sol,data.MCMCglmm.3$VCV)) + ) > > summary(data.mcmc.list)
Iterations = 1:4700
Thinning interval = 1
Number of chains = 3
Sample size per chain = 4700
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
(Intercept) 41.08 0.838 0.00706 0.00715
Aa2 14.66 1.190 0.01002 0.01038
Bb2 4.65 1.171 0.00986 0.00986
Bb3 -0.73 1.189 0.01001 0.00984
Aa2:Bb2 -15.73 1.664 0.01402 0.01417
Aa2:Bb3 9.31 1.674 0.01410 0.01410
units 7.01 1.410 0.01187 0.01187
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
(Intercept) 39.43 40.52 41.086 41.6365 42.72
Aa2 12.35 13.87 14.663 15.4562 17.03
Bb2 2.35 3.88 4.653 5.4261 6.96
Bb3 -3.07 -1.51 -0.739 0.0645 1.62
Aa2:Bb2 -19.00 -16.84 -15.733 -14.6049 -12.43
Aa2:Bb3 5.97 8.21 9.324 10.4196 12.57
units 4.77 6.01 6.834 7.8265 10.22
> > nIter=150000 > thinSteps=10 > comparisonTab <- cbind(comparisonTab,'MCMCglmm'=comTab(data.mcmc.list,cols="Intercept|A|B|unit",lag=10,MCMCglmm.time)) >
rcppbugs
> library(rcppbugs) > > b <- mcmc.normal(rnorm(6),mu=0,tau=0.0001) > tau.y <- mcmc.gamma(runif(1),alpha=0.1,beta=0.1) > X <- model.matrix(~A*B, data) > y.hat <- linear(X,b) > #or > y.hat <- deterministic(function(X,b) { X %*% b }, X, b) > > y.lik <- mcmc.normal(data$y,mu=y.hat,tau=tau.y,observed=TRUE) > m <- create.model(b, tau.y, y.hat, y.lik) > > ## then to run the model: > cat("running model...\n")
running model...
> rcppbugs.time <- system.time( + ans <- run.model(m, iterations=500000, burn=30000, adapt=1e3L, thin=500) + ) > ## and view the 'trace' of b > #print(ans[["b"]]) > > summary(as.mcmc(ans$b))
Iterations = 1:1000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 1000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
[1,] 41.138 0.83 0.0262 0.0295
[2,] 14.671 1.20 0.0379 0.0440
[3,] 4.586 1.13 0.0358 0.0428
[4,] -0.812 1.20 0.0380 0.0416
[5,] -15.765 1.64 0.0519 0.0643
[6,] 9.341 1.68 0.0531 0.0610
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
var1 39.54 40.61 41.148 41.7188 42.75
var2 12.35 13.84 14.663 15.4575 17.13
var3 2.43 3.82 4.541 5.3699 6.82
var4 -3.30 -1.62 -0.826 0.0182 1.64
var5 -19.12 -16.81 -15.768 -14.6479 -12.63
var6 5.86 8.19 9.418 10.4815 12.44
> data.mcmc <- as.mcmc(cbind(ans$b, 1/ans$tau.y)) > colnames(data.mcmc) <- c("beta1","beta2","beta3","beta4","beta5","beta6","sigma") > > nIter=500000 > thinSteps=500 > comparisonTab <- cbind(comparisonTab,'rcppbugs'=comTab(data.mcmc,cols="beta|sigma",lag=1,rcppbugs.time)) >
Python
> X <- model.matrix(~A * B, data = data) > dataP <- cbind(data$y, X) > write.csv(dataP, "../downloads/data/factorialAnova.csv")
import pandas as pd
import numpy as np
from pymc import *
pd.set_option('html', False)
data = pd.read_csv('../downloads/data/factorialAnova.csv')
#print data.head()
Y = data.y
X = data.iloc[:,2:7]
beta = Normal('beta_%s', mu=0.0, tau=100000**-1, value=np.zeros(5))
sigma = Uniform('sigma', lower=0, upper=1000)
tau = Lambda('tau', lambda sd=sigma: sd**-2)
# Model
mu = Lambda('mu', lambda b=beta: np.dot(X,b))
#mu = LinearCombination('mu',[X],[beta],doc='mu=Xb')
# Likelihood
Yi = Normal('Yi',mu=mu,tau=tau,observed=True,value=Y)
alpha = beta[1]+beta[0]
mdl= Model([Yi,tau,sigma,beta])
M = MCMC(mdl)
M.sample(50000,40000,thin=100,progress_bar=False)
print M.stats()
print M.summary()
Matplot.plot(M)
Quick glance Bayesian regression model specification
| JAGS | Stan | MCMCregress | MCMCglmm | rcppbugs | |
|---|---|---|---|---|---|
| Iterations | 166667 | 53000 | 150000 | 150000 | 5e+05 |
| Thinning | 10 | 10 | 10 | 10 | 500 |
| Samples | 49401 | 15000 | 15000 | 14100 | 1000 |
| Maximum ACF | 0.0079 | 0.0169 | 0.0183 | 0.0191 | 0.16 |
| (Intercept) | 41.10 [39.46 , 42.77] | 41.10 [39.41 , 42.76] | 41.10 [39.49 , 42.77] | 41.09 [39.43 , 42.72] | 41.15 [39.59 , 42.78] |
| beta2 | 14.65 [12.37 , 17.02] | 14.64 [12.39 , 17.07] | 14.65 [12.34 , 16.99] | 14.66 [12.26 , 16.94] | 14.66 [12.48 , 17.17] |
| beta3 | 4.63 [2.35 , 7.00] | 4.64 [2.31 , 7.04] | 4.63 [2.29 , 6.97] | 4.65 [2.43 , 7.01] | 4.54 [2.27 , 6.66] |
| beta4 | -0.75 [-3.14 , 1.52] | -0.76 [-3.17 , 1.52] | -0.77 [-3.02 , 1.64] | -0.74 [-3.06 , 1.62] | -0.83 [-3.00 , 1.86] |
| beta5 | -15.71 [-18.97 , -12.41] | -15.71 [-19.01 , -12.43] | -15.73 [-19.10 , -12.46] | -15.73 [-19.05 , -12.51] | -15.77 [-19.12 , -12.61] |
| beta6 | 9.34 [5.94 , 12.58] | 9.34 [6.05 , 12.62] | 9.34 [6.16 , 12.72] | 9.32 [6.03 , 12.60] | 9.42 [6.04 , 12.59] |
| sigma | 2.62 [2.15 , 3.16] | 2.64 [2.18 , 3.19] | 6.82 [4.51 , 9.78] | 6.83 [4.45 , 9.75] | 6.77 [4.72 , 10.12] |
| Time (user self) | 23.09 | 17.05 | 0.79 | 3.00 | 2.80 |
| Time (system self) | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 |
| Time (elapsed) | 23.12 | 45.46 | 0.80 | 3.04 | 2.81 |
| Time (user child) | 0.00 | 27.43 | 0.00 | 0.00 | 0.00 |
| Time (system child) | 0.00 | 0.65 | 0.00 | 0.00 | 0.00 |
| Model | JAGS | rstan |
|---|---|---|
| Matrix effects parameterization |
model {
#Likelihood
for (i in 1:n) {
y[i]~dnorm(mean[i],tau)
mean[i] <- inprod(beta[],X[i,])
}
#Priors and derivatives
for (i in 1:p) {
beta[i] ~ dnorm(0, 1.0E-6) #prior
}
sigma ~ dgamma(0.001, 0.001)
tau <- 1 / (sigma * sigma)
}
|
data {
int<lower=0> n;
int<lower=0> p;
vector[n] y;
matrix [n,p] X;
}
parameters {
vector[p] beta;
real<lower=0> sigma;
}
model {
vector[n] mu;
#Priors
beta ~ normal(0.01, 100000);
sigma~ uniform(0,100);
#Likelihood
mu <- X*beta;
y ~ normal(mu, sigma);
}
|
Finite population standard deviations
Prior to creating code to do all sorts of matrix manipulations, we will first define a new function to calculate finite-population standard deviation.
The sd() function calculates population standard deviations from samples according to the regular formula: $$\sigma = \frac{\sum{(x_i - \bar{x})^2}}{n-1}$$ where $n$ is the sample size. Division by $n-1$ is intended to reduce the bias in the estimated population standard deviation given that the mean is also calculated from the same sample.
In order to be able to sensibly compare standard deviations between 'fixed' and 'random' factors, all factors need to be considered as 'fixed' for the purpose of standard deviation calculations. That is, we need to assume that we have sampled from all possible levels available.
> sdP <- function(x) { + m <- mean(x) + sqrt((sum((x - m)^2))/length(x)) + }
- Method 1 - create specific model matrices to generate specific cell means
for each of the main effects and interactions from which we can
calculate the finite-population standard deviation.
> data.fpsd <- NULL > # Get the contrasts used for each Factor > contr <- attr(model.matrix(~A * B, data), "contrasts") > ## Get the effects parameter samples > library(coda) > coefs <- as.matrix(Data.mcmc.list)[, 1:6] > > # A > dt <- data > dt$B <- "b1" > cc <- model.frame(~A * B, dt, xlev = list(A = levels(data$A), B = levels(data$B))) > X1 <- model.matrix(~A * B, cc, contrasts = contr) > a <- coefs[, 1:6] %*% t(X1) > data.fpsd <- rbind(data.fpsd, A = MCMCsum(apply(a, 1, sdP))) > # MCMCsum(apply(t(apply(a,1,function(x) x-t(data$y))), 1, sdP)) > > dt <- data > dt$A <- "a1" > cc <- model.frame(~A * B, dt, xlev = list(A = levels(data$A), B = levels(data$B))) > X1 <- model.matrix(~A * B, cc, contrasts = contr) > a <- coefs[, 1:6] %*% t(X1) > data.fpsd <- rbind(data.fpsd, B = MCMCsum(apply(a, 1, sdP))) > # MCMCsum(apply(t(apply(a,1,function(x) x-t(data$y))), 1, sdP)) > > > dt <- data #expand.grid(A=levels(data$A), B=levels(data$B)) > cc <- model.frame(~A * B, dt, xlev = list(A = levels(data$A), B = levels(data$B))) > X1 <- model.matrix(~A * B, cc, contrasts = contr) > a <- coefs[, 1:6] %*% t(X1) > data.fpsd <- rbind(data.fpsd, `A:B` = MCMCsum(apply(a, 1, sdP))) > > # Residuals > data.Xmat <- model.matrix(~A * B, data) > a <- coefs[, 1:6] %*% t(data.Xmat) > data.fpsd <- rbind(data.fpsd, Resid = MCMCsum(apply(t(apply(a, 1, function(x) x - t(data$y))), 1, sdP))) > > data.fpsd
Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 A 7.326 4.3800 6.929 7.326 7.718 9.987 6.161 8.490 6.707 7.876 B 2.432 0.5893 2.113 2.432 2.749 4.788 1.487 3.362 1.974 2.919 A:B 8.653 7.0894 8.425 8.653 8.882 10.126 7.997 9.344 8.312 8.983 Resid 2.565 2.4662 2.526 2.565 2.618 3.409 2.473 2.729 2.488 2.609
- Method 2 - incorporate the finite population standard deviation
calculations as derived quantities (posteriors) into the Bayesian model.
> modelString = "\nmodel {\n #Likelihood\n for (i in 1:n) {\n y[i]~dnorm(mean[i],tau)\n mean[i] <- inprod(beta[],X[i,])\n y.err[i] <- y[i] - mean[i]\n }\n #Priors and derivatives\n for (i in 1:p) {\n beta[i] ~ dnorm(0, 1.0E-6) #prior\n }\n sigma ~ dgamma(0.001, 0.001)\n tau <- 1 / (sigma * sigma)\n\n sd.A <- abs(beta[2])*sd(X[,2])\n sd.B <- sd(beta[3:4])\n sd.AB <- sd(beta[5:6])\n sd.resid <- sd(y.err)\n }\n" > writeLines(modelString, con = "../downloads/BUGSscripts/junk.txt") > X <- model.matrix(~A * B, data) > data.list <- with(data, list(y = y, X = X, n = nrow(data), p = ncol(X))) > > params <- c("beta", "sigma", "sd.A", "sd.B", "sd.AB", "sd.resid") > adaptSteps = 1000 > burnInSteps = 2000 > nChains = 3 > numSavedSteps = 50000 > thinSteps = 10 > nIter = ceiling((numSavedSteps * thinSteps)/nChains) > library(R2jags) > rnorm(1)
[1] 1.594
> jags.effects.simple.time <- system.time(data.r2jagsA <- jags(data = data.list, inits = NULL, parameters.to.save = params, model.file = "../downloads/BUGSscripts/junk.txt", n.chains = 3, n.iter = nIter, + n.burnin = burnInSteps, n.thin = thinSteps))
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 572 Initializing model
> print(data.r2jagsA)
Inference for Bugs model at "../downloads/BUGSscripts/junk.txt", fit using jags, 3 chains, each with 166667 iterations (first 2000 discarded), n.thin = 10 n.sims = 49401 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff beta[1] 41.098 0.835 39.444 40.544 41.100 41.654 42.752 1.001 49000 beta[2] 14.649 1.185 12.316 13.856 14.644 15.438 16.997 1.001 49000 beta[3] 4.641 1.180 2.317 3.862 4.642 5.424 6.957 1.001 49000 beta[4] -0.747 1.185 -3.082 -1.541 -0.747 0.040 1.593 1.001 49000 beta[5] -15.718 1.672 -19.025 -16.826 -15.712 -14.600 -12.442 1.001 49000 beta[6] 9.335 1.678 6.040 8.215 9.333 10.450 12.636 1.001 49000 sd.A 7.325 0.593 6.158 6.928 7.322 7.719 8.498 1.001 49000 sd.AB 12.527 0.842 10.874 11.961 12.529 13.085 14.177 1.001 49000 sd.B 2.694 0.591 1.531 2.300 2.693 3.088 3.855 1.001 32000 sd.resid 2.580 0.075 2.484 2.526 2.564 2.618 2.769 1.001 49000 sigma 2.635 0.261 2.187 2.451 2.613 2.795 3.208 1.001 49000 deviance 286.007 3.987 280.342 283.077 285.321 288.168 295.572 1.001 49000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 7.9 and DIC = 294.0 DIC is an estimate of expected predictive error (lower deviance is better). - Method 3 - calculating the finite-population standard deviations
from the parameter samples.
> data.fpsd1 <- NULL > > ## Get the effects parameter samples > library(coda) > coefs <- as.matrix(Data.mcmc.list)[, 1:6] > # sd A > data.fpsd1 <- rbind(data.fpsd1, A = MCMCsum(apply(cbind(0, coefs[, 2]), 1, sdP))) > # sd B > data.fpsd1 <- rbind(data.fpsd1, B = MCMCsum(apply(coefs[, 3:4], 1, sdP))) > # sd AB > data.fpsd1 <- rbind(data.fpsd1, `A:B` = MCMCsum(apply(coefs[, 5:6], 1, sdP))) > # sd Resid > data.Xmat <- model.matrix(~A * B, data) > a <- coefs[, 1:6] %*% t(data.Xmat) > data.fpsd1 <- rbind(data.fpsd1, Resid = MCMCsum(apply(t(apply(a, 1, function(x) x - t(data$y))), 1, sdP))) > > data.fpsd1
Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 A 7.326 4.38004 6.929 7.326 7.718 9.987 6.161 8.490 6.707 7.876 B 2.696 0.04553 2.299 2.696 3.093 5.303 1.547 3.869 2.119 3.289 A:B 12.526 9.05699 11.965 12.526 13.083 16.195 10.868 14.169 11.704 13.353 Resid 2.565 2.46622 2.526 2.565 2.618 3.409 2.473 2.729 2.488 2.609
| Via specific matricies | Via MCMC samples |
|---|---|
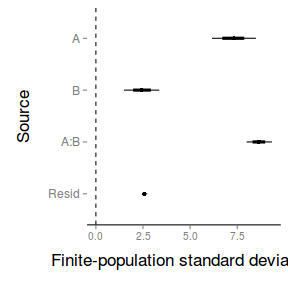 |
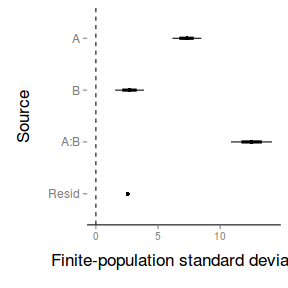 |
Conclusions - there is clear evidence of a strong interactions between Factor A and Factor B. There is very little residual variability. In the presence of a strong interaction, it is not really appropriate to make statements about the main effects (similar to frequentist ANOVA).
Dealing with interactions
- Start by generating posteriors for the cell means (means of each factor combination) using the MCMC effects parameter samples.
> ## Get the effects parameter samples > library(coda) > coefs <- as.matrix(Data.mcmc.list)[, 1:6] > ## Calculate the model matrix > dt <- expand.grid(A = gl(2, 1, 2, lab = c("a1", "a2")), B = gl(3, 1, 3, lab = paste("b", 1:3, sep = ""))) > Xmat <- model.matrix(~A * B, dt) > # OR using actual data frame---------------------------------------------- > Xmat <- model.matrix(~A * B, data) > library(plyr) > Xmat <- as.matrix(ddply(data.frame(Xmat), ~interaction(data$A, data$B), colwise(mean))[, -1]) > ## ------------------------------------------------------------------------ > cellmeans.mcmc <- coefs %*% t(Xmat) > colnames(cellmeans.mcmc) <- unique(interaction(data$A, data$B)) > head(cellmeans.mcmc)
a1.b1 a2.b1 a1.b2 a2.b2 a1.b3 a2.b3 [1,] 42.56 56.64 45.55 42.79 40.65 63.92 [2,] 41.48 54.76 45.32 44.87 39.80 64.60 [3,] 40.54 57.91 45.63 43.47 40.97 62.15 [4,] 41.17 55.94 45.90 43.60 40.21 65.58 [5,] 41.41 56.90 45.40 45.92 40.06 63.52 [6,] 40.21 56.56 45.50 43.65 40.25 63.34
- Work out which means you want to compare for any particular comparison.
> ## a2 vs a1 at b1 (columns 2 vs 1) > comps <- cellmeans.mcmc[, 2] - cellmeans.mcmc[, 1] > MCMCsum(comps)
Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 var1 14.65 8.76 13.86 14.65 15.44 19.97 12.32 16.98 13.41 15.75
> > comps <- cellmeans.mcmc[, c(2, 4)] - cellmeans.mcmc[, c(1, 3)] > library(plyr) > adply(comps, 2, MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 a2.b1 14.652 8.760 13.859 14.652 15.4352 19.975 12.32 16.980 13.415 15.7510 2 a2.b2 -1.064 -6.575 -1.852 -1.064 -0.2744 4.457 -3.35 1.301 -2.193 0.1391
Alternatively, we could generate a new model matrix to enter in the matrix multiplication.
> dt <- expand.grid(A = gl(2, 1, 2, lab = c("a1", "a2")), B = gl(3, 1, 3, lab = paste("b", 1:3, sep = ""))) > Xmat <- model.matrix(~A * B, dt) > contr <- attr(Xmat, "contrasts") > cc <- model.frame(~A * B, expand.grid(A = "a1", B = levels(dt$B)), xlev = list(A = levels(dt$A), B = levels(dt$B))) > X1 <- model.matrix(~A * B, cc, contrasts = contr) > cc <- model.frame(~A * B, expand.grid(A = "a2", B = levels(dt$B)), xlev = list(A = levels(dt$A), B = levels(dt$B))) > X2 <- model.matrix(~A * B, cc, contrasts = contr) > Xmat <- X2 - X1 > > comps <- coefs %*% t(Xmat) > adply(comps, 2, MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 1 14.652 8.760 13.859 14.652 15.4352 19.975 12.32 16.980 13.415 15.7510 2 2 -1.064 -6.575 -1.852 -1.064 -0.2744 4.457 -3.35 1.301 -2.193 0.1391 3 3 23.986 18.693 23.188 23.986 24.7809 28.781 21.71 26.336 22.754 25.0940
We could also setup a contrast matrix to compare every factor combination to every other combination. Of course, many of these comparisons would be of very little value, yet since they come at no statistical cost and virtually no CPU cost, we might as well compute them.
> library(multcomp) > dt <- expand.grid(A = gl(2, 1, 2, lab = c("a1", "a2")), B = gl(3, 1, 3, lab = paste("b", 1:3, sep = ""))) > Xmat <- contrMat(n = rep(1, 6), type = "Tukey") %*% model.matrix(~A * B, dt) > > wch <- ldply(strsplit(rownames(Xmat), " - "), as.numeric) > rownames(Xmat) <- paste(interaction(dt$A, dt$B)[wch[, 1]], "-", interaction(dt$A, dt$B)[wch[, 2]]) > pairwise.comps <- coefs %*% t(Xmat) > adply(pairwise.comps, 2, MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 a2.b1 - a1.b1 14.652 8.7601 13.859 14.652 15.43517 19.97466 12.323 16.980 13.415 15.7510 2 a1.b2 - a1.b1 4.640 -0.4678 3.849 4.640 5.43066 10.41009 2.359 7.015 3.468 5.7973 3 a2.b2 - a1.b1 3.584 -1.4835 2.784 3.584 4.36833 9.21229 1.213 5.890 2.426 4.7643 4 a1.b3 - a1.b1 -0.753 -5.7112 -1.545 -0.753 0.04267 4.60223 -3.119 1.560 -1.985 0.3477 5 a2.b3 - a1.b1 23.236 16.9283 22.443 23.236 24.02545 28.58819 20.960 25.625 22.096 24.4334 6 a1.b2 - a2.b1 -10.008 -15.1043 -10.800 -10.008 -9.21427 -3.02951 -12.345 -7.689 -11.152 -8.8161 7 a2.b2 - a2.b1 -11.069 -16.6425 -11.859 -11.069 -10.29079 -5.84443 -13.428 -8.765 -12.230 -9.9030 8 a1.b3 - a2.b1 -15.403 -20.1645 -16.197 -15.403 -14.60353 -10.06412 -17.740 -13.056 -16.609 -14.2743 9 a2.b3 - a2.b1 8.583 2.5642 7.788 8.583 9.36127 14.47940 6.276 10.928 7.427 9.7446 10 a2.b2 - a1.b2 -1.064 -6.5748 -1.852 -1.064 -0.27435 4.45700 -3.350 1.301 -2.193 0.1391 11 a1.b3 - a1.b2 -5.393 -10.6058 -6.185 -5.393 -4.59728 -0.09107 -7.738 -3.094 -6.577 -4.2387 12 a2.b3 - a1.b2 18.592 13.1093 17.796 18.592 19.37964 23.68861 16.230 20.900 17.439 19.7637 13 a1.b3 - a2.b2 -4.330 -9.4606 -5.117 -4.330 -3.53601 1.28821 -6.676 -2.047 -5.516 -3.1866 14 a2.b3 - a2.b2 19.663 14.0185 18.875 19.663 20.43900 24.98024 17.356 22.009 18.514 20.8492 15 a2.b3 - a1.b3 23.986 18.6933 23.188 23.986 24.78088 28.78113 21.709 26.336 22.754 25.0940
Unbalanced designs
Unlike in frequentist modelling, in Bayesian statistics, design balance does not present any additional challenges (above the potential impacts on variance homogeneity. In order to illustrate this, we will modify the current data set by removing a few replicates from specific cells.
> data1 <- data[c(-3, -6, -12), ] > with(data1, table(A, B))
B A b1 b2 b3 a1 10 9 10 a2 10 10 8
> ## If the following function returns a list (implying that the number of replicates is different for different combinations of factors), then the design is NOT balanced > replications(~A * B, data1)
$A
A
a1 a2
29 28
$B
B
b1 b2 b3
20 19 18
$`A:B`
B
A b1 b2 b3
a1 10 9 10
a2 10 10 8
> modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mean[i],tau) mean[i] <- inprod(beta[],X[i,]) } #Priors and derivatives for (i in 1:p) { beta[i] ~ dnorm(0, 1.0E-6) #prior } sigma ~ dgamma(0.001, 0.001) tau <- 1 / (sigma * sigma) } " > writeLines(modelString,con="../downloads/BUGSscripts/tut9.6bS9.2.txt") > X <- model.matrix(~A*B, data1) > data.list1 <- with(data1, + list(y=y, + X=X, + n=nrow(data1), + p=ncol(X) + ) + ) > > params <- c("beta","sigma") > adaptSteps = 1000 > burnInSteps = 2000 > nChains = 3 > numSavedSteps = 50000 > thinSteps = 10 > nIter = ceiling((numSavedSteps * thinSteps)/nChains) > > library(R2jags) > rnorm(1)
[1] 0.9133
> > jags.effects.simple.time <- system.time( + data.r2jags1 <- jags(data=data.list1, + inits=NULL, + parameters.to.save=params, + model.file="../downloads/BUGSscripts/tut9.6bS9.2.txt", + n.chains=3, + n.iter=nIter, + n.burnin=burnInSteps, + n.thin=thinSteps + ) + )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 478 Initializing model
> print(data.r2jags1)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.6bS9.2.txt", fit using jags,
3 chains, each with 166667 iterations (first 2000 discarded), n.thin = 10
n.sims = 49401 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 41.090 0.842 39.428 40.531 41.088 41.651 42.742 1.001 49000
beta[2] 14.656 1.192 12.302 13.861 14.653 15.451 16.994 1.001 49000
beta[3] 5.002 1.224 2.586 4.181 5.007 5.825 7.403 1.001 46000
beta[4] -0.745 1.189 -3.093 -1.538 -0.746 0.048 1.592 1.001 49000
beta[5] -16.074 1.713 -19.443 -17.212 -16.077 -14.936 -12.714 1.001 49000
beta[6] 9.325 1.734 5.903 8.177 9.320 10.484 12.754 1.001 49000
sigma 2.648 0.268 2.189 2.458 2.626 2.813 3.233 1.001 31000
deviance 272.110 3.989 266.444 269.176 271.433 274.274 281.681 1.001 19000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 8.0 and DIC = 280.1
DIC is an estimate of expected predictive error (lower deviance is better).
> data.mcmc.list1 <- as.mcmc(data.r2jags1) > > ## Get the effects parameter samples > library(coda) > coefs <- as.matrix(data.mcmc.list1)[, 1:6] > ## Calculate the model matrix > dt <- expand.grid(A = gl(2, 1, 2, lab = c("a1", "a2")), B = gl(3, 1, 3, lab = paste("b", 1:3, sep = ""))) > Xmat <- model.matrix(~A * B, dt) > # OR using actual data frame---------------------------------------------- > Xmat <- model.matrix(~A * B, data1) > library(plyr) > Xmat <- as.matrix(ddply(data.frame(Xmat), ~interaction(data1$A, data1$B), colwise(mean))[, -1]) > ## ------------------------------------------------------------------------ > cellmeans.mcmc1 <- coefs %*% t(Xmat) > colnames(cellmeans.mcmc1) <- unique(interaction(data1$A, data1$B)) > adply(cellmeans.mcmc1, 2, MCMCsum)
X1 Median X0. X25. X50. X75. X100. lower upper lower.1 upper.1 1 a1.b1 41.09 37.38 40.53 41.09 41.65 44.65 39.43 42.75 40.27 41.93 2 a2.b1 55.74 51.82 55.18 55.74 56.31 59.86 54.08 57.38 54.91 56.56 3 a2.b2 46.09 41.90 45.50 46.09 46.68 50.13 44.28 47.80 45.23 46.98 4 a1.b3 44.68 40.72 44.11 44.68 45.23 48.31 43.01 46.34 43.77 45.44 5 a1.b2 40.35 36.98 39.79 40.35 40.90 44.12 38.70 42.00 39.53 41.18 6 a2.b3 64.33 60.00 63.70 64.33 64.96 68.71 62.51 66.21 63.42 65.28
Conclusions - these values are practically the same as previous estimates based on a full balanced design!
