Tutorial 7.2b - Simple linear regression (Bayesian)
12 Jan 2018
- Chapter 7 of
Kery (2010) - Chapters 3 and 4 of
McCarthy (2007) - Chapters 11 and 12 of
Gelman and Hill (2007) - Chapters 1, 2 and 6 of
Logan (2010) - Chapters 1, 2, 3 and 4 of
Quinn and Keough (2002) - http://onlinelibrary.wiley.com/doi/10.1111/2041-210X.12681/full
Many biologists and ecologists get a little twitchy and nervous around mathematical and statistical formulae and nomenclature. Whilst it is possible to perform basic statistics without too much regard for the actual equation (model) being employed, as the complexity of the analysis increases, the need to understand the underlying model becomes increasingly important. Moreover, model specification in BUGS (the language used to program Bayesian modelling) aligns very closely to the underlying formulae. Hence a good understanding of the underlying model is vital to be able to create a sensible Bayesian model. Consequently, I will always present the linear model formulae along with the analysis. If you start to feel some form of disorder starting to develop, you might like to run through the Tutorials and Workshops twice (the first time ignoring the formulae).
Overview
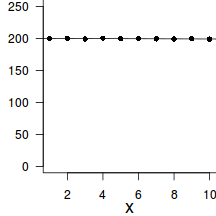
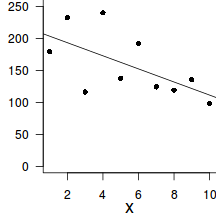
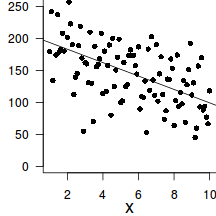
To introduce the philosophical and mathematical differences between classical (frequentist) and Bayesian statistics, Wade (2000) presented a provocative yet compelling trend analysis of two hypothetical populations. The temporal trend of one of the populations shows very little variability from a very subtle linear decline. By contrast, the second population appears to decline more dramatically, yet has substantially more variability.
Wade (2000) neatly illustrates the contrasting conclusions (particularly with respect to interpreting probability) that would be drawn by the frequentist and Bayesian approaches and in so doing highlights how and why the Bayesian approach provides outcomes that are more aligned with management requirements.
This tutorial will start by replicating the demonstration of Wade (2000). Thereafter, we will replicate the fabricated analysis of Tutorial 7.2a
 |
 |
 |
|
n: |
n: |
n: |
From a traditional frequentist perspective, we would conclude that there is a 'significant' relationship in Population A and C ($p<0.05$), yet not in Population B ($p>0.05$). Note, Population B and C were both generated from the same random distribution, it is just that Population C has a substantially higher number of observations.
The above illustrates a couple of things
- statistical significance does not necessarily translate into biological importance.
The percentage of decline for Population A is
0.46where as the percentage of decline for Population B is45.26. That is Population B is declining at nearly 10 times the rate of Population A. That sounds rather important, yet on the basis of the hypothesis test, we would dismiss the decline in Population B. - that a p-value is just the probability of detecting an effect or relationship - what is the probability that the sample size is large enough to pick up a difference.
Let us now look at it from a Bayesian perspective. I will just provide the posterior distributions (densities scaled to 0-1 so that they can be plotted together) for the slope for each population.
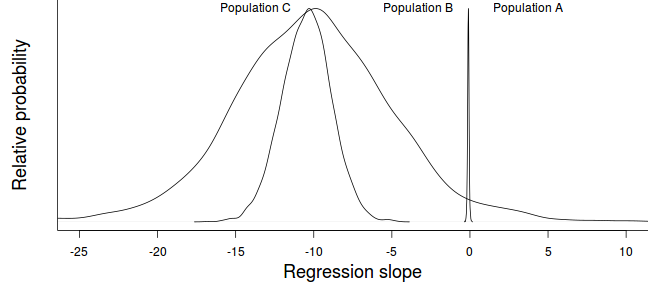
Focusing on Populations A and B, we would conclude:
- the mean (plus or minus CI) slopes for Population A and B are
-0.1(-0.21,0) and-10.08(-20.32,0.57) respectively. - the Bayesian approach allows us to query the posterior distribution is many other ways in order to ask sensible biological questions.
For example, we might consider that a rate of change of 5% or greater represents an important biological impact.
For Population A and B, the probability that the rate is 5% or greater is
0and0.85respectively.
Simple linear regression is a linear modelling process that models a continuous response against a single continuous predictor. The linear model is expressed as: $$y_i = \beta_0+ \beta_1 x_i+\epsilon_i \hspace{1cm}\epsilon\sim{}N(0,\sigma^2)$$ where:
- $y_i$ is the response value for each of the $i$ observations
- $\beta_0$ is the y-intercept (value of $y$ when $x=0$)
- $\beta_1$ is the slope (rate of chance in $y$ per unit chance in $x$)
- $x_i$ is the predictor value for each of the $i$ observations
- $\epsilon_i$ is the residual value of each of the $i$ observations. A residual is the difference between the observed value and the value expected by the model.
- $\epsilon\sim{}N(0,\sigma^2)$ indicates that the residuals are normally distributed with a constant amount of variance
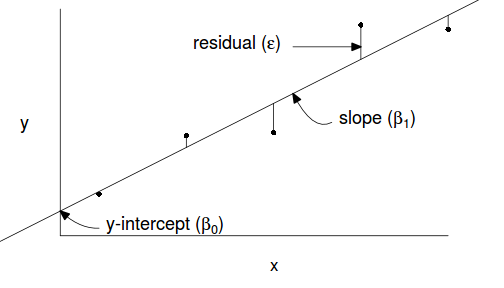
The parameters of the trendline ($\beta_0, \beta_1$) are determined by Ordinary Least Squares in which the sum of the squared residuals is minimized. A non-zero population slope is indicative of a relationship.
Scenario and Data
Lets say we had set up an experiment in which we applied a continuous treatment ($x$) ranging in magnitude from 0 to 16 to a total of 16 sampling units ($n=16$) and then measured a response ($y$) from each unit. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the sample size = 16
- the continuous $x$ variable ranging from 0 to 16
- when the value of $x$ is 0, $y$ is expected to be 40 ($\beta_0=40$)
- a 1 unit increase in $x$ is associated with a 1.5 unit decline in $y$ ($\beta_1=-1.5$)
- the data are drawn from normal distributions with a mean of 0 and standard deviation of 5 ($\sigma^2=25$)
set.seed(1) n <- 16 a <- 40 #intercept b <- -1.5 #slope sigma2 <- 25 #residual variance (sd=5) x <- 1:n #values of the year covariate eps <- rnorm(n, mean = 0, sd = sqrt(sigma2)) #residuals y <- a + b * x + eps #response variable # OR y <- (model.matrix(~x) %*% c(a, b)) + eps data <- data.frame(y, x) #dataset head(data) #print out the first six rows of the data set
y x 1 35.36773 1 2 37.91822 2 3 31.32186 3 4 41.97640 4 5 34.14754 5 6 26.89766 6
With these sort of data, we are primarily interested in investigating whether there is a relationship between the continuous response variable and the linear predictor (single continuous predictor).
Centering data
When a linear model contains a covariate (continuous predictor variable) in addition to another predictor (continuous or categorical), it is nearly always advisable that the continuous predictor variables be centered prior to the analysis. Centering is a process by which the mean of a variable is subtracted from each of the values such that the scale of the variable is shifted so as to be centered around 0. Hence the mean of the new centered variable will be 0, yet it will retain the same variance.
Raw data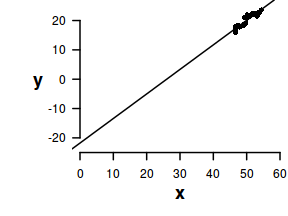
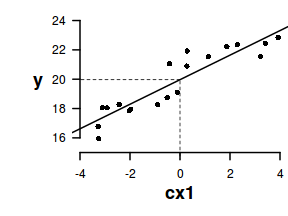
There are multiple reasons for this:
- Firstly, it provides some biological meaning to the y-intercept. Recall that the y-intercept is the value of Y when X is equal to zero. If X is centered, then the y-intercept represents the value of Y at the mid-point of the X range. The y-intercept of an un-centered X typically represents a un-real value of Y (as an X of 0 is often beyond the reasonable range of values).
- Secondly, in multiplicative models (in which predictors and their interactions are included), main effects and interaction terms built from centered predictors will not be correlated to one another (see below)
- Thirdly, for more complex models, centering the covariates can increase the likelihood that the modelling engine converges (arrives at a numerically stable and reliable outcome).
In R, centering is easily achieved with the scale function.
data <- within(data, { cx1 <- as.numeric(scale(x1, scale = FALSE)) cx2 <- as.numeric(scale(x2, scale = FALSE)) }) head(data)
Exploratory data analysis and initial assumption checking
Normality
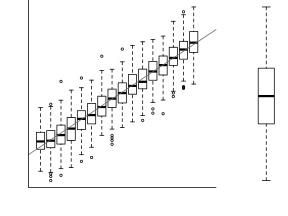
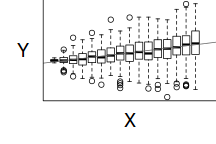
Estimation and inference testing in linear regression assumes that the response is normally distributed in each of the populations. In this case, the populations are all possible measurements that could be collected at each level of $x$ - hence there are 16 populations. Typically however, we only collect a single observation from each population (as is also the case here). How then can be evaluate whether each of these populations are likely to have been normal?
 |
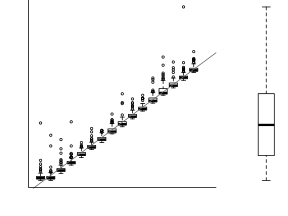 |
For a given response, the population distributions should follow much the same distribution shapes. Therefore provided the single samples from each population are unbiased representations of those populations, a boxplot of all observations should reflect the population distributions.
The two figures above show the relationships between the individual population distributions and the overall distribution. The left hand figure shows a distribution drawn from single representatives of each of the 16 populations. Since the 16 individual populations were normally distributed, the distribution of the 16 observations is also normal.
By contrast, the right hand figure shows 16 log-normally distributed populations and the resulting distribution of 16 single observations drawn from these populations. The overall boxplot mirrors each of the individual population distributions.
Homogeneity of variance
Simple linear regression also assumes that each of the populations are equally varied. Actually, it is prospect of a relationship between the mean and variance of y-values across x-values that is of the greatest concern. Strictly the assumption is that the distribution of y values at each x value are equally varied and that there is no relationship between mean and variance.
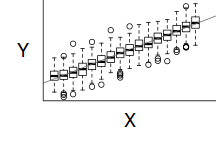
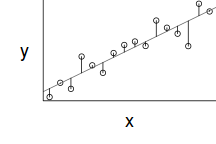
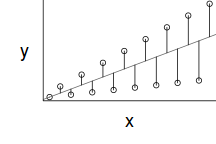
However, as we only have a single y-value for each x-value, it is difficult to directly determine whether the assumption of homogeneity of variance is likely to have been violated (mean of one value is meaningless and variability can't be assessed from a single value). The figure below depicts the ideal (and almost never realistic) situation in which (left hand figure) the populations are all equally varied. The middle figure simulates drawing a single observation from each of the populations. When the populations are equally varied, the spread of observed values around the trend line is fairly even - that is, there is no trend in the spread of values along the line.
If we then plot the residuals (difference between observed values and those predicted by the trendline) against the predict values, there is a definite lack of pattern. This lack of pattern is indicative of a lack of issues with homogeneity of variance.
 |
 |
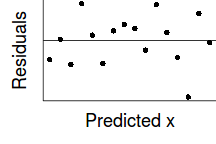 |
If we now contrast the above to a situation where the population variance is related to the mean (unequal variance), we see that the observations drawn from these populations are not evenly distributed along the trendline (they get more spread out as the mean predicted value increase). This pattern is emphasized in the residual plot which displays a characteristic "wedge"-shape pattern.
 |
 |
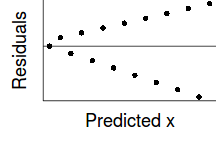 |
Hence looking at the spread of values around a trendline on a scatterplot of $y$ against $x$ is a useful way of identifying gross violations of homogeneity of variance. Residual plots provide an even better diagnostic. The presence of a wedge shape is indicative that the population mean and variance are related.
Linearity
Linear regression fits a straight (linear) line through the data. Therefore, prior to fitting such a model, it is necessary to establish whether this really is the most sensible way of describing the relationship. That is, does the relationship appear to be linearly related or could some other non-linear function describe the relationship better. Scatterplots and residual plots are useful diagnostics
Explore assumptions
- All of the observations are independent - this must be addressed at the design and collection stages
- The response variable (and thus the residuals) should be normally distributed
- The response variable should be equally varied (variance should not be related to mean as these are supposed to be estimated separately)
- the relationship between the linear predictor (right hand side of the regression formula) and the link function should be linear. A scatterplot with smoother can be useful for identifying possible non-linearity.
So lets explore normality, homogeneity of variances and linearity by constructing a scatterplot of the relationship between the response ($y$) and the predictor ($x$). We will also include a range of smoothers (linear and lowess) and marginal boxplots on the scatterplot to assist in exploring linearity and normality respectively.
# scatterplot library(car) scatterplot(y ~ x, data)
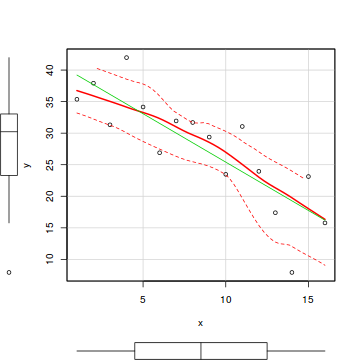
Conclusions:
- there is no evidence that the response variable is non-normal
- the spread of values around the trendline seems fairly even (hence it there is no evidence of non-homogeneity
- the data seems well represented by the linear trendline. Furthermore, the lowess smoother does not appear to have a consistent shift trajectory.
- consider a non-linear linear predictor (such as a polynomial, spline or other non-linear function)
- transform the scale of the response variables (to address normality etc)
Model fitting or statistical analysis
As with Tutorial 6.2b we will explore Bayesian modelling of simple linear regression using a variety of tools (such as MCMCpack, JAGS, RSTAN, RSTANARM and BRMS). Whilst JAGS and RSTAN are extremely flexible and thus allow models to be formulated that contain not only the simple model, but also additional derivatives, the other approaches are more restrictive. Consequently, I will mostly restrict models to just the minimum necessary and all derivatives will instead be calculated in R itself from the returned posteriors. Hence for each model, I will generate a mcmc list (data.mcmc.list) containing the mcmc sample matrix for each chain. This mcmc list will be considered a standard starting point for all other manipulations.
The purpose of fitting a model in this case is to explore the relationship between y and x. Since both y and x are continuous, a simple regression line is a good start.
The observed response ($y_i$) are assumed to be drawn from a normal distribution with a given mean ($\mu$) and standard deviation ($\sigma$). The expected values ($\mu$) are themselves determined by the linear predictor ($\beta_0 + \beta x_i$). In this case, $\beta_0$ represents the y-intercept (value of $y$ when $x$ is equal to zero) and $\beta$ represents the rate of change in $y$ for every unit change in $x$ (the effect).
Note that in this form, the y-intercept is of little interest. Indeed for many applications, a value of $x$ would be outside the domain of the collected data, outside the logical bounds of the actual variable or else outside the domain of interest. If however, we center the predictor variable (by subtracting the mean of $x$ from each $x$, then the y-intercept represents the value of $y$ at the average value of $x$. This certainly has more meaning. Note that centering the predictor does not effect the estimate of slope.
MCMC sampling requires priors on all parameters. We will employ weakly informative priors. Specifying 'uninformative' priors is always a bit of a balancing act. If the priors are too vague (wide) the MCMC sampler can wander off into nonscence areas of likelihood rather than concentrate around areas of highest likelihood (desired when wanting the outcomes to be largely driven by the data). On the other hand, if the priors are too strong, they may have an influence on the parameters. In such a simple model, this balance is very forgiving - it is for more complex models that prior choice becomes more important.
For this simple model, we will go with zero-centered Gaussian (normal) priors with relatively large standard deviations (1000) for both the intercept and the treatment effect and a wide half-cauchy (scale=25) for the standard deviation. $$ \begin{align} y_i &\sim{} N(\mu, \sigma)\\ \mu &= \beta_0 + \beta x_i\\[1em] \beta_0 &\sim{} N(0,1000)\\ \beta &\sim{} N(0,1000)\\ \sigma &\sim{} cauchy(0,25)\\ \end{align} $$
library(MCMCpack) data.mcmcpack <- MCMCregress(y ~ x, data = data)
Structure of the JAGS model
Define the model
We now translate the likelihood model into BUGS/JAGS code and store the code in an external file.
$y_i\sim{}N(\mu_i, \tau)\\
\mu_i = \beta_0+\beta_1 x_i\\
\beta_0\sim{}N(0,1.0{E-6}) \hspace{1cm}\mathsf{non-informative~prior}\\
\beta_1\sim{}N(0,1.0{E-6}) \hspace{1cm}\mathsf{non-informative~prior}\\
\tau = 1/\sigma^2\\
\sigma\sim{}U(0,100)\\
$
- the percentage decline ($100*\frac{((max(x)-min(x))*\beta)+min(y)}{min{y}}$) and the probability that $y$ decline by more than 25%.
- the finite-population variance components
modelString = " model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- beta0+beta1*x[i] y.err[i] <- y[i] - mu[i] } #Priors beta0 ~ dnorm(0.01,1.0E-6) beta1 ~ dnorm(0,1.0E-6) tau <- 1 / (sigma * sigma) sigma~dunif(0,100) } " ## write the model to <a href=''></a> text file (I ## suggest you alter the path to somewhere more ## relevant to your system!) writeLines(modelString, con = "../downloads/BUGSscripts/tut7.2bS4.1.txt")
modelString = " model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- beta0+beta1*x[i] y.err[i] <- y[i] - mu[i] } #Priors beta0 ~ dnorm(0.01,1.0E-6) beta1 ~ dnorm(0,1.0E-6) tau <- 1 / (sigma * sigma) sigma~dunif(0,100) #Other Derived parameters p.decline <- 1-step(beta1) ymin<-beta0+beta1*min(x) xrange <- max(x) - min(x) decline <- 100*((xrange*beta1)+ymin)/ymin p.decline25 <- step(decline-25) #finite-population variance components sd.x <- abs(beta1)*sd(x[]) sd.resid <- sd(y.err) } " ## write the model to <a href=''></a> text file (I ## suggest you alter the path to somewhere more ## relevant to your system!) writeLines(modelString, con = "../downloads/BUGSscripts/tut7.2bS4.1a.txt")
Define the data list
Arrange the data as a list (as required by BUGS). As input, JAGS will need to be supplied with:
- the response variable (y)
- the predictor variable (x)
- the total number of observed items (n)
data.list <- with(data, list(y = y, x = x, n = nrow(data))) data.list
$y [1] 35.367731 37.918217 31.321857 41.976404 [5] 34.147539 26.897658 31.937145 31.691624 [9] 29.378907 23.473058 31.058906 23.949216 [13] 17.393797 7.926501 23.124655 15.775332 $x [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 16 $n [1] 16
Define the initial values
Define the initial values ($\beta_0$, $\beta_1$ and $\sigma^2$ for the chain. Reasonable starting points can be gleaned from the data themselves. Note, this step is not absolutely necessary for simple models as the R2jags interface will automatically create sensible initial values for the parameters based on simple data summaries.
inits <- rep(list(list(beta0 = mean(data$y), beta1 = diff(tapply(data$y, data$x, mean)), sigma = sd(data$y))), 3)
Define the MCMC chain parameters
Next we should define the behavioural parameters of the MCMC sampling chains. Include the following:
- the nodes (estimated parameters) to monitor (return samples for)
- the number of MCMC chains (3)
- the number of burnin steps (1000)
- the thinning factor (10)
- the number of MCMC iterations - determined by the number of samples to save, the rate of thinning and the number of chains
params <- c("beta0", "beta1", "sigma") nChains = 3 burnInSteps = 3000 thinSteps = 10 numSavedSteps = 15000 #across all chains nIter = ceiling(burnInSteps + (numSavedSteps * thinSteps)/nChains) nIter
[1] 53000
Fit the model
Now run the JAGS code via the R2jags interface. Note that the first time jags is run after the R2jags package is loaded, it is often necessary to run any kind of randomization function just to initiate the .Random.seed variable.
## load the R2jags package library(R2jags)
data.r2jags <- jags(data = data.list, inits = NULL, parameters.to.save = params, model.file = "../downloads/BUGSscripts/tut7.2bS4.1.txt", n.chains = nChains, n.iter = nIter, n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph Resolving undeclared variables Allocating nodes Graph information: Observed stochastic nodes: 16 Unobserved stochastic nodes: 3 Total graph size: 119 Initializing model
print(data.r2jags)
Inference for Bugs model at "../downloads/BUGSscripts/tut7.2bS4.1.txt", fit using jags,
3 chains, each with 53000 iterations (first 3000 discarded), n.thin = 10
n.sims = 15000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta0 40.776 3.012 34.771 38.854 40.754 42.700 46.732 1.001 6500
beta1 -1.536 0.309 -2.155 -1.739 -1.534 -1.339 -0.917 1.001 8800
sigma 5.612 1.198 3.825 4.765 5.433 6.244 8.454 1.001 15000
deviance 98.913 2.916 95.586 96.795 98.131 100.243 106.547 1.001 15000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 4.3 and DIC = 103.2
DIC is an estimate of expected predictive error (lower deviance is better).
data.mcmc.list <- as.mcmc(data.r2jags)
Whilst Gibbs sampling provides an elegantly simple MCMC sampling routine, very complex hierarchical models can take enormous numbers of iterations (often prohibitory large) to converge on a stable posterior distribution.
To address this, Andrew Gelman (and other collaborators) have implemented a variation on Hamiltonian Monte Carlo (HMC: a sampler that selects subsequent samples in a way that reduces the correlation between samples, thereby speeding up convergence) called the No-U-Turn (NUTS) sampler. All of these developments are brought together into a tool called Stan ("Sampling Through Adaptive Neighborhoods").
By design (to appeal to the vast BUGS users), Stan models are defined in a manner reminiscent of BUGS. Stan first converts these models into C++ code which is then compiled to allow very rapid computation.
Consistent with the use of C++, the model must be accompanied by variable declarations for all inputs and parameters.
One important difference between Stan and JAGS is that whereas BUGS (and thus JAGS) use precision rather than variance, Stan uses variance.
Stan itself is a stand-alone command line application. However, conveniently, the authors of Stan have also developed an R interface to Stan called Rstan which can be used much like R2jags.
Structure of a stan model
Note the following important characteristics of stan code:
- A stan model file comprises a number of blocks (not all of which are compulsory).
- The stan language is an intermediary between (R/BUGS and c++), stan requires all types (integers, vectors, matrices etc) to be declared prior to use and it uses c++ commenting (// and /* */)
- Code order is important, objects must be declared before they are used. When a type is declared in one block, it is available in subsequent blocks.
data {
// declare the input data / parameters
}
transformed data {
// optional - for transforming/scaling input data
}
parameters {
// define model parameters
}
transformed parameters {
// optional - for deriving additional non-model parameters
// note however, as they are part of the sampling chain
// transformed parameters slow sampling down.
}
model {
// specifying priors and likelihood as well as the linear predictor
}
generated quantities {
// optional - derivatives (posteriors) of the samples
}
Define the model
The minimum model in Stan required to fit the above simple regression follows. Note the following modifications from the model defined in JAGS:- the normal distribution is defined by variance rather than precision
- rather than using a uniform prior for sigma, I am using a half-Cauchy
We now translate the likelihood model into STAN code.
$y_i\sim{}N(\mu_i, \sigma)\\
\mu_i = \beta_0+\beta_1 x_i\\
\beta_0\sim{}N(0,1000)\\
\beta_1\sim{}N(0,1000)\\
\sigma\sim{}Cauchy(0,5)\\
$
modelString = " data { int<lower=0> n; vector [n] y; vector [n] x; } parameters { real beta0; real beta; real<lower=0> sigma; } model { vector [n] mu; #Priors beta0 ~ normal(0,10000); beta ~ normal(0,10000); sigma ~ cauchy(0,5); mu = beta0+beta*x; #Likelihood y~normal(mu,sigma); } " ## write the model to a text file (I suggest you alter the path to somewhere more relevant to your ## system!) writeLines(modelString, con = "../downloads/BUGSscripts/tut7.2bS11.1.txt")
modelString1 = " data { int<lower=0> n; real y[n]; real x[n]; } parameters { real beta0; real beta; real<lower=0> sigma; } transformed parameters { real mu[n]; for (i in 1:n) mu[i] = beta0+beta*x[i]; } model { #Likelihood y~normal(mu,sigma); #Priors beta0 ~ normal(0,10000); beta ~ normal(0,10000); sigma~uniform(0,100); } "
The No-U-Turn sampler operates much more efficiently if all predictors are centered. Although it is possible to pre-center all predictors that are passed to STAN, it is then often necessary to later convert back to the original scale for graphing and further analyses. Since centering is a routine procedure, arguably it should be built into the STAN we generate. Furthermore, we should also include the back-scaling as well. The following code is inspired by the code generated by the BRMS package.
data {
int<lower=1> n; // total number of observations
vector[n] Y; // response variable
int<lower=1> nX; // number of effects
matrix[n, nX] X; // model matrix
}
transformed data {
matrix[n, nX - 1] Xc; // centered version of X
vector[nX - 1] means_X; // column means of X before centering
for (i in 2:nX) {
means_X[i - 1] = mean(X[, i]);
Xc[, i - 1] = X[, i] - means_X[i - 1];
}
}
parameters {
vector[nX-1] beta; // population-level effects
real cbeta0; // center-scale intercept
real<lower=0> sigma; // residual SD
}
transformed parameters {
}
model {
vector[n] mu;
mu = Xc * beta + cbeta0;
// prior specifications
beta ~ normal(0, 100);
cbeta0 ~ normal(0, 100);
sigma ~ cauchy(0, 5);
// likelihood contribution
Y ~ normal(mu, sigma);
}
generated quantities {
real beta0; // population-level intercept
beta0 = cbeta0 - dot_product(means_X, beta);
}
In this version, the data are to be supplied as a model matrix (so as to leverage various vectorized and matrix multiplier routines). The transformed data block is used to center the non-intercept columns of the predictor model matrix. The model is fit on centered data thereby generating a slope and intercept. This intercept parameter is also expressed back on the non-centered scale (generated properties block).
Define the data list
Arrange the data as a list (as required by BUGS). As input, Stan (like WinBUGS/JAGS) will need to be supplied with:
- the response variable (y)
- the predictor variable (x)
- the total number of observed items (n)
Xmat <- model.matrix(~x, data = data) data.list <- with(data, list(Y = y, X = Xmat, nX = ncol(Xmat), n = nrow(data))) data.list
$Y [1] 35.367731 37.918217 31.321857 41.976404 34.147539 26.897658 31.937145 31.691624 29.378907 [10] 23.473058 31.058906 23.949216 17.393797 7.926501 23.124655 15.775332 $X (Intercept) x 1 1 1 2 1 2 3 1 3 4 1 4 5 1 5 6 1 6 7 1 7 8 1 8 9 1 9 10 1 10 11 1 11 12 1 12 13 1 13 14 1 14 15 1 15 16 1 16 attr(,"assign") [1] 0 1 $nX [1] 2 $n [1] 16
Define the MCMC chain parameters
Next we should define the behavioural parameters of the No-U-Turn sampling chains. Include the following:
- the nodes (estimated parameters) to monitor (return samples for)
- the number of MCMC chains (3)
- the number of burnin steps (1000)
- the thinning factor (10)
- the number of MCMC iterations - determined by the number of samples to save, the rate of thinning and the number of chains
nChains = 3 burnInSteps = 1000 thinSteps = 3 numSavedSteps = 3000 #across all chains nIter = ceiling(burnInSteps + (numSavedSteps * thinSteps)/nChains) nIter
[1] 4000
Fit the model
Now compile and run the Stan code via the rstan interface. Note that the first time jags is run after the rstan package is loaded, it is often necessary to run any kind of randomization function just to initiate the .Random.seed variable.
During the warmup stage, the No-U-Turn sampler (NUTS) attempts to determine the optimum stepsize - the stepsize that achieves the target acceptance rate (0.8 or 80% by default) without divergence (occurs when the stepsize is too large relative to the curvature of the log posterior - and results in approximations that are likely to diverge and be biased) and without hitting the maximum treedepth (10). At each iteration of the NUTS algorithm, the number of leapfrog steps doubles (as it increases the treedepth) and only terminates when either the NUTS criterion are satisfied or the tree depth reaches the maximum (10 by default).
## load the rstan package library(rstan)
data.rstan <- stan(data = data.list, model_code = modelString, chains = nChains, iter = nIter, warmup = burnInSteps, thin = thinSteps, save_dso = TRUE)
In file included from /usr/local/lib/R/site-library/BH/include/boost/config.hpp:39:0,
from /usr/local/lib/R/site-library/BH/include/boost/math/tools/config.hpp:13,
from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/core/var.hpp:7,
from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/core/gevv_vvv_vari.hpp:5,
from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/core.hpp:12,
from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4,
from /usr/local/lib/R/site-library/StanHeaders/include/stan/math.hpp:4,
from /usr/local/lib/R/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4,
from file6ff34d65b11c.cpp:8:
/usr/local/lib/R/site-library/BH/include/boost/config/compiler/gcc.hpp:186:0: warning: "BOOST_NO_CXX11_RVALUE_REFERENCES" redefined
# define BOOST_NO_CXX11_RVALUE_REFERENCES
^
<command-line>:0:0: note: this is the location of the previous definition
SAMPLING FOR MODEL 'e7d4e08d9f1bbcf9d6d79f126f9e56c7' NOW (CHAIN 1).
Gradient evaluation took 1.4e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.14 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 4000 [ 0%] (Warmup)
Iteration: 400 / 4000 [ 10%] (Warmup)
Iteration: 800 / 4000 [ 20%] (Warmup)
Iteration: 1001 / 4000 [ 25%] (Sampling)
Iteration: 1400 / 4000 [ 35%] (Sampling)
Iteration: 1800 / 4000 [ 45%] (Sampling)
Iteration: 2200 / 4000 [ 55%] (Sampling)
Iteration: 2600 / 4000 [ 65%] (Sampling)
Iteration: 3000 / 4000 [ 75%] (Sampling)
Iteration: 3400 / 4000 [ 85%] (Sampling)
Iteration: 3800 / 4000 [ 95%] (Sampling)
Iteration: 4000 / 4000 [100%] (Sampling)
Elapsed Time: 0.018545 seconds (Warm-up)
0.045305 seconds (Sampling)
0.06385 seconds (Total)
SAMPLING FOR MODEL 'e7d4e08d9f1bbcf9d6d79f126f9e56c7' NOW (CHAIN 2).
Gradient evaluation took 5e-06 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 4000 [ 0%] (Warmup)
Iteration: 400 / 4000 [ 10%] (Warmup)
Iteration: 800 / 4000 [ 20%] (Warmup)
Iteration: 1001 / 4000 [ 25%] (Sampling)
Iteration: 1400 / 4000 [ 35%] (Sampling)
Iteration: 1800 / 4000 [ 45%] (Sampling)
Iteration: 2200 / 4000 [ 55%] (Sampling)
Iteration: 2600 / 4000 [ 65%] (Sampling)
Iteration: 3000 / 4000 [ 75%] (Sampling)
Iteration: 3400 / 4000 [ 85%] (Sampling)
Iteration: 3800 / 4000 [ 95%] (Sampling)
Iteration: 4000 / 4000 [100%] (Sampling)
Elapsed Time: 0.017913 seconds (Warm-up)
0.04733 seconds (Sampling)
0.065243 seconds (Total)
SAMPLING FOR MODEL 'e7d4e08d9f1bbcf9d6d79f126f9e56c7' NOW (CHAIN 3).
Gradient evaluation took 6e-06 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 4000 [ 0%] (Warmup)
Iteration: 400 / 4000 [ 10%] (Warmup)
Iteration: 800 / 4000 [ 20%] (Warmup)
Iteration: 1001 / 4000 [ 25%] (Sampling)
Iteration: 1400 / 4000 [ 35%] (Sampling)
Iteration: 1800 / 4000 [ 45%] (Sampling)
Iteration: 2200 / 4000 [ 55%] (Sampling)
Iteration: 2600 / 4000 [ 65%] (Sampling)
Iteration: 3000 / 4000 [ 75%] (Sampling)
Iteration: 3400 / 4000 [ 85%] (Sampling)
Iteration: 3800 / 4000 [ 95%] (Sampling)
Iteration: 4000 / 4000 [100%] (Sampling)
Elapsed Time: 0.018588 seconds (Warm-up)
0.043631 seconds (Sampling)
0.062219 seconds (Total)
The STAN team has put together pre-compiled modules (functions) to make specifying and applying STAN models much simpler. Each function offers a consistent interface that is Also reminiscent of major frequentist linear modelling routines in R.
Whilst it is not necessary to specify priors when using rstanarm functions (as defaults will be generated), there is no guarantee that the routines for determining these defaults will persist over time. Furthermore, it is always better to define your own priors if for no other reason that it forces you to thing about what you are doing. Consistent with the pure STAN version, we will employ the following priors:
- weakly informative Gaussian prior for the intercept $\beta_0 \sim{} N(0, 1000)$
- weakly informative Gaussian prior for the treatment effect $\beta_1 \sim{} N(0, 1000)$
- half-cauchy prior for the variance $\sigma \sim{} Cauchy(0, 25)$
Note, I am using the refresh=0 option so as to suppress the larger regular output in the interest of keeping output to what is necessary for this tutorial. When running outside of a tutorial context, the regular verbose output is useful as it provides a way to gauge progress.
library(rstanarm) data.rstanarm = stan_glm(y ~ x, data = data, iter = 2000, warmup = 200, chains = 3, thin = 2, refresh = 0, prior_intercept = normal(0, 1000), prior = normal(0, 1000), prior_aux = cauchy(0, 25))
Gradient evaluation took 2.2e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.22 seconds.
Adjust your expectations accordingly!
Elapsed Time: 1.80628 seconds (Warm-up)
0.807009 seconds (Sampling)
2.61329 seconds (Total)
Gradient evaluation took 1e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Adjust your expectations accordingly!
Elapsed Time: 1.98795 seconds (Warm-up)
1.66692 seconds (Sampling)
3.65488 seconds (Total)
Gradient evaluation took 9e-06 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
Adjust your expectations accordingly!
Elapsed Time: 1.52452 seconds (Warm-up)
0.845179 seconds (Sampling)
2.36969 seconds (Total)
print(data.rstanarm)
stan_glm
family: gaussian [identity]
formula: y ~ x
------
Estimates:
Median MAD_SD
(Intercept) 40.8 2.9
x -1.5 0.3
sigma 5.4 1.1
Sample avg. posterior predictive
distribution of y (X = xbar):
Median MAD_SD
mean_PPD 27.7 2.0
------
For info on the priors used see help('prior_summary.stanreg').
library(broom) library(coda) tidyMCMC(data.rstanarm, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 (Intercept) 40.734015 3.0668570 34.412462 46.3425366 2 x -1.531248 0.3148917 -2.123538 -0.8981083 3 sigma 5.619764 1.1740461 3.604894 7.9675118
The brms package serves a similar goal to the rstanarm package - to provide a simple user interface to STAN. However, unlike the rstanarm implementation, brms simply converts the formula, data, priors and family into STAN model code and data before executing stan with those elements.
Whilst it is not necessary to specify priors when using brms functions (as defaults will be generated), there is no guarantee that the routines for determining these defaults will persist over time. Furthermore, it is always better to define your own priors if for no other reason that it forces you to thing about what you are doing. Consistent with the pure STAN version, we will employ the following priors:
- weakly informative Gaussian prior for the intercept $\beta_0 \sim{} N(0, 1000)$
- weakly informative Gaussian prior for the treatment effect $\beta_1 \sim{} N(0, 1000)$
- half-cauchy prior for the variance $\sigma \sim{} Cauchy(0, 25)$
Note, I am using the refresh=0. option so as to suppress the larger regular output in the interest of keeping output to what is necessary for this tutorial. When running outside of a tutorial context, the regular verbose output is useful as it provides a way to gauge progress.
library(brms) data.brms = brm(y ~ x, data = data, iter = 2000, warmup = 200, chains = 3, thin = 2, refresh = 0, prior = c(prior(normal(0, 1000), class = "Intercept"), prior(normal(0, 1000), class = "b"), prior(cauchy(0, 25), class = "sigma")))
Gradient evaluation took 1.2e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
Adjust your expectations accordingly!
Elapsed Time: 0.006342 seconds (Warm-up)
0.02702 seconds (Sampling)
0.033362 seconds (Total)
Gradient evaluation took 2.5e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.25 seconds.
Adjust your expectations accordingly!
Elapsed Time: 0.006317 seconds (Warm-up)
0.026596 seconds (Sampling)
0.032913 seconds (Total)
Gradient evaluation took 5e-06 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
Adjust your expectations accordingly!
Elapsed Time: 0.005054 seconds (Warm-up)
0.028559 seconds (Sampling)
0.033613 seconds (Total)
print(data.brms)
Family: gaussian(identity)
Formula: y ~ x
Data: data (Number of observations: 16)
Samples: 3 chains, each with iter = 2000; warmup = 200; thin = 2;
total post-warmup samples = 2700
ICs: LOO = Not computed; WAIC = Not computed
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept 40.85 3.07 34.90 47.24 2310 1
x -1.55 0.32 -2.18 -0.90 2408 1
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sigma 5.63 1.19 3.9 8.48 2091 1
Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
is a crude measure of effective sample size, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
library(broom) library(coda) tidyMCMC(data.brms$fit, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 b_Intercept 40.853729 3.0714471 34.407211 46.6638946 2 b_x -1.545095 0.3205355 -2.141672 -0.8693169 3 sigma 5.631356 1.1888245 3.779939 8.2153548
MCMC diagnostics
In addition to the regular model diagnostic checks (such as residual plots), for Bayesian analyses, it is necessary to explore the characteristics of the MCMC chains and the sampler in general. Recall that the purpose of MCMC sampling is to replicate the posterior distribution of the model likelihood and priors by drawing a known number of samples from this posterior (thereby formulating a probability distribution). This is only reliable if the MCMC samples accurately reflect the posterior.
Unfortunately, since we only know the posterior in the most trivial of circumstances, it is necessary to rely on indirect measures of how accurately the MCMC samples are likely to reflect the likelihood. I will breifly outline the most important diagnostics, however, please refer to Tutorial 4.3, Secton 3.1: Markov Chain Monte Carlo sampling for a discussion of these diagnostics.
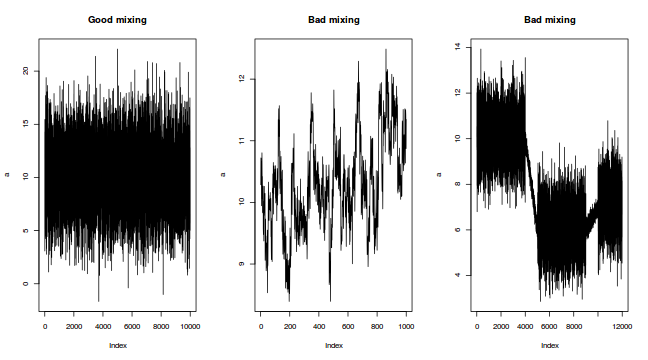
- Traceplots for each parameter illustrate the MCMC sample values after each successive
iteration along the chain. Bad chain mixing (characterized by any sort of pattern) suggests
that the MCMC sampling chains may not have completely traversed all features of the posterior
distribution and that more iterations are required to ensure the distribution has been accurately
represented.
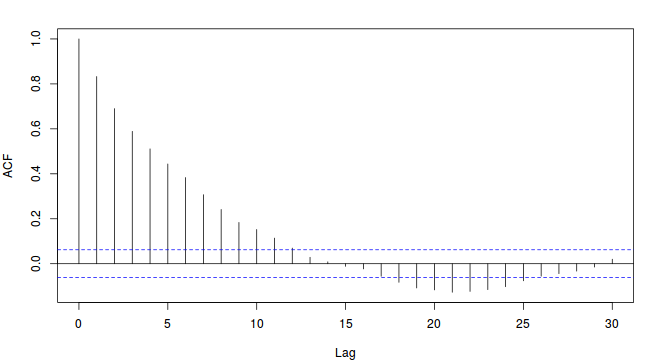
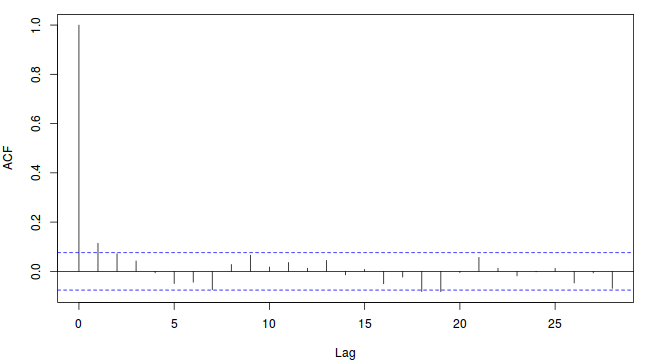
- Autocorrelation plot for each paramter illustrate the degree of correlation between
MCMC samples separated by different lags. For example, a lag of 0 represents the degree of
correlation between each MCMC sample and itself (obviously this will be a correlation of 1).
A lag of 1 represents the degree of correlation between each MCMC sample and the next sample along the Chain
and so on. In order to be able to generate unbiased estimates of parameters, the MCMC samples should be
independent (uncorrelated). In the figures below, this would be violated in the top autocorrelation plot and met in the bottom
autocorrelation plot.
- Rhat statistic for each parameter provides a measure of sampling efficiency/effectiveness. Ideally, all values should be less than 1.05. If there are values of 1.05 or greater it suggests that the sampler was not very efficient or effective. Not only does this mean that the sampler was potentiall slower than it could have been, more importantly, it could indicate that the sampler spent time sampling in a region of the likelihood that is less informative. Such a situation can arise from either a misspecified model or overly vague priors that permit sampling in otherwise nonscence parameter space.
Prior to inspecting any summaries of the parameter estimates, it is prudent to inspect a range of chain convergence diagnostics
- Trace plots
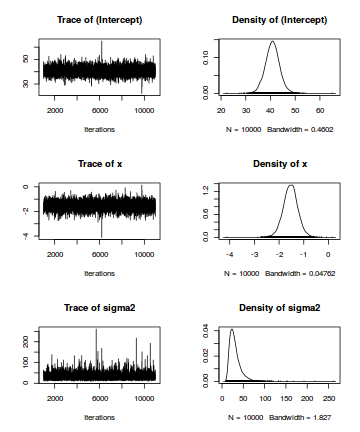
View trace plotsTrace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
library(MCMCpack) plot(data.mcmcpack)
- Raftery diagnostic
View Raftery diagnosticThe Raftery diagnostics estimate that we would require about 3900 samples to reach the specified level of confidence in convergence. As we have 10,000 samples, we can be confidence that convergence has occurred.
library(MCMCpack) raftery.diag(data.mcmcpack)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) (Intercept) 3 4028 3746 1.080 x 2 3851 3746 1.030 sigma2 2 3680 3746 0.982 - Autocorrelation diagnostic
View autocorrelationsA lag of 1 appears to be mainly sufficient to avoid autocorrelation (except for sigma2, which is over 0.1). The diagnostic suggests that a lag of 5 would potentially correct this.
library(MCMCpack) autocorr.diag(data.mcmcpack)
(Intercept) x sigma2 Lag 0 1.000000000 1.000000000 1.000000000 Lag 1 0.011287106 -0.000965701 0.162987189 Lag 5 -0.004110531 0.004773571 0.008242103 Lag 10 -0.015174763 -0.012219328 0.002405411 Lag 50 -0.003762082 -0.007068066 -0.009647390
Again, prior to examining the summaries, we should have explored the convergence diagnostics.
library(coda) data.mcmc = as.mcmc(data.r2jags)
- Trace plots
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
plot(data.mcmc)
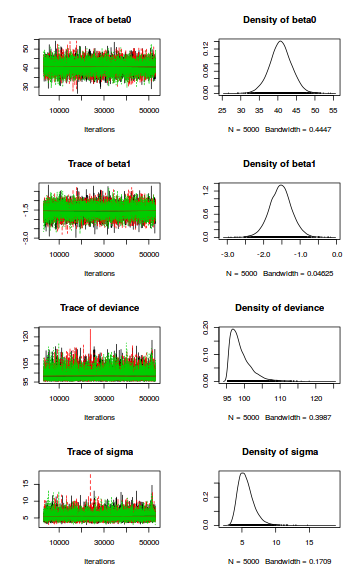
When there are a lot of parameters, this can result in a very large number of traceplots. To focus on just certain parameters (such as $\beta$s)
preds <- c("beta0", "beta1") plot(as.mcmc(data.r2jags)[, preds])
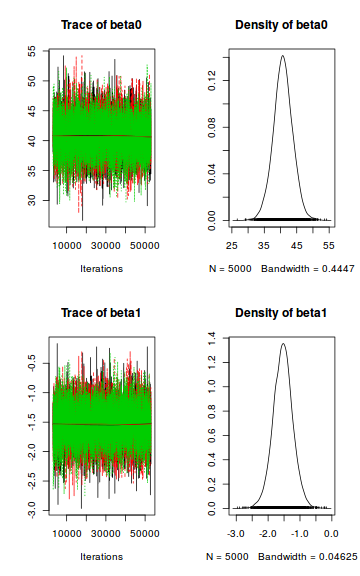
- Raftery diagnostic
The Raftery diagnostics for each chain estimate that we would require no more than 5000 samples to reach the specified level of confidence in convergence. As we have 16,667 samples, we can be confidence that convergence has occurred.
raftery.diag(data.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) beta0 20 38660 3746 10.30 beta1 20 36200 3746 9.66 deviance 20 36800 3746 9.82 sigma 20 36200 3746 9.66 [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) beta0 20 37410 3746 9.99 beta1 20 38660 3746 10.30 deviance 20 36800 3746 9.82 sigma 20 36800 3746 9.82 [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) beta0 20 38030 3746 10.20 beta1 20 38030 3746 10.20 deviance 20 36200 3746 9.66 sigma 20 35610 3746 9.51 - Autocorrelation diagnostic
A lag of 10 appears to be sufficient to avoid autocorrelation (poor mixing).
autocorr.diag(data.mcmc)
beta0 beta1 deviance sigma Lag 0 1.000000000 1.000000000 1.000000000 1.0000000000 Lag 10 0.002343329 -0.006499521 -0.005759350 0.0008347558 Lag 50 -0.009224921 -0.010877289 -0.003269510 0.0022530505 Lag 100 -0.004536817 0.002460483 0.007360297 0.0108817122 Lag 500 -0.002154409 0.003107960 -0.004786948 -0.0052312783
Again, prior to examining the summaries, we should have explored the convergence diagnostics. There are numerous ways of working with STAN model fits (for exploring diagnostics and summarization).
- extract the mcmc samples and convert them into a mcmc.list to leverage the various coda routines
- use the numerous routines that come with the rstan package
- use the routines that come with the bayesplot package
- explore the diagnostics interactively via shinystan
- via coda
- Traceplots
- Autocorrelation
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.library(coda) s = as.array(data.rstan) mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(mcmc)
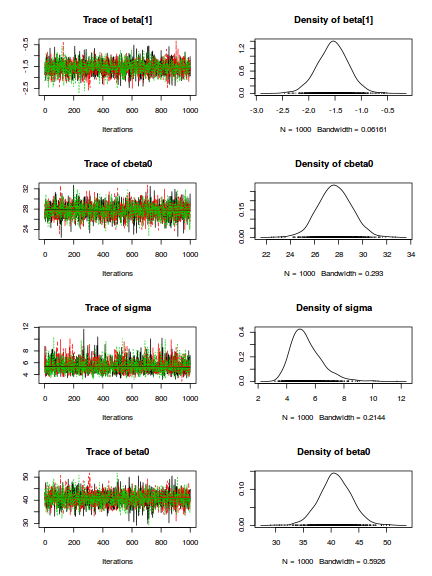 Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.library(coda) s = as.array(data.rstan) mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) autocorr.diag(mcmc)
beta[1] cbeta0 sigma beta0 Lag 0 1.000000000 1.000000000 1.000000000 1.00000000 Lag 1 0.016316577 0.020651289 0.036121993 0.00965383 Lag 5 -0.006799616 -0.039385336 -0.006821465 -0.02197035 Lag 10 0.012913933 0.006045351 -0.018816878 0.01012661 Lag 50 -0.028343488 0.015861053 0.007679815 -0.00919722
- via rstan
- Traceplots
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
stan_trace(data.rstan)
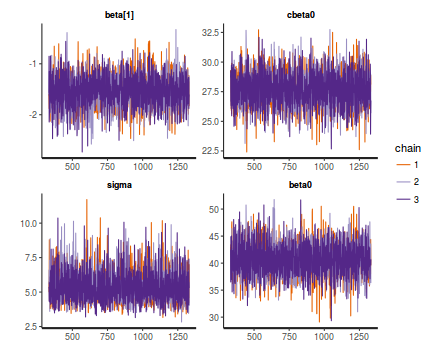
- Raftery diagnostic
The Raftery diagnostics for each chain estimate that we would require no more than 5000 samples to reach the specified level of confidence in convergence. As we have 16,667 samples, we can be confidence that convergence has occurred.
raftery.diag(data.rstan)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
- Autocorrelation diagnostic
A lag of 2 appears broadly sufficient to avoid autocorrelation (poor mixing).
stan_ac(data.rstan)
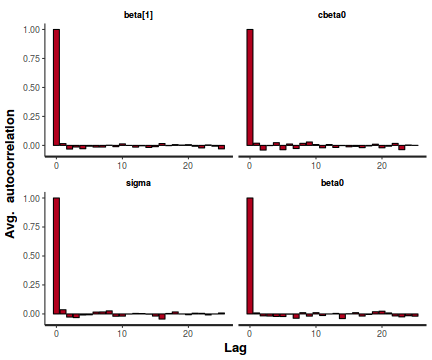
- Rhat values. These values are a measure of sampling efficiency/effectiveness. Ideally, all values should be less than 1.05.
If there are values of 1.05 or greater it suggests that the sampler was not very efficient or effective. Not only does this
mean that the sampler was potentiall slower than it could have been, more importantly, it could indicate that the sampler spent time sampling
in a region of the likelihood that is less informative. Such a situation can arise from either a misspecified model or
overly vague priors that permit sampling in otherwise nonscence parameter space.
In this instance, all rhat values are well below 1.05 (a good thing).
stan_rhat(data.rstan)
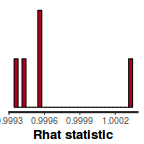
- Another measure of sampling efficiency is Effective Sample Size (ess).
ess indicate the number samples (or proportion of samples that the sampling algorithm deamed effective. The sampler rejects samples
on the basis of certain criterion and when it does so, the previous sample value is used. Hence while the MCMC sampling chain
may contain 1000 samples, if there are only 10 effective samples (1%), the estimated properties are not likely to be reliable.
In this instance, most of the parameters have reasonably high effective samples and thus there is likely to be a good range of values from which to estimate paramter properties.
stan_ess(data.rstan)
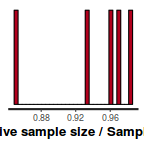
- Traceplots
- via bayesplot
- Trace plots and density plots
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
library(bayesplot) mcmc_trace(as.array(data.rstan), regex_pars = "beta|sigma")
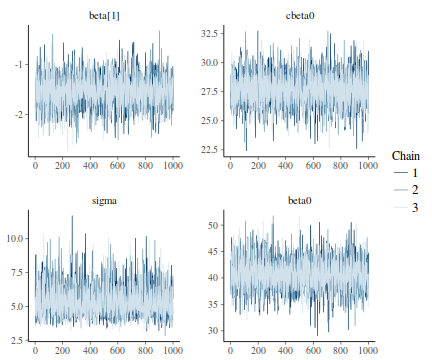
library(bayesplot) mcmc_combo(as.array(data.rstan))
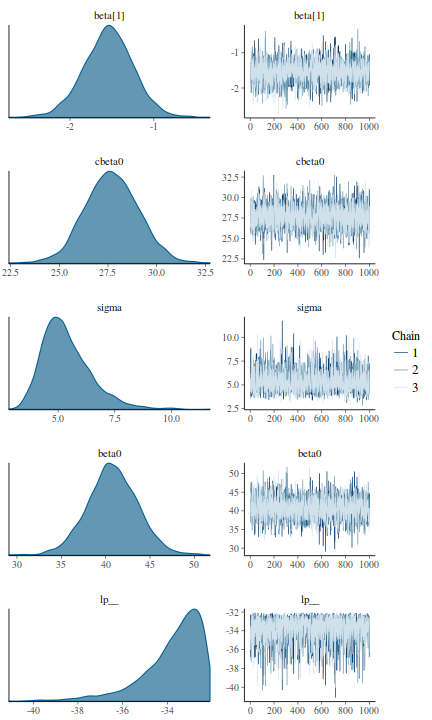
- Density plots
Density plots sugggest mean or median would be appropriate to describe the fixed posteriors and median is appropriate for the sigma posterior.
library(bayesplot) mcmc_dens(as.array(data.rstan))
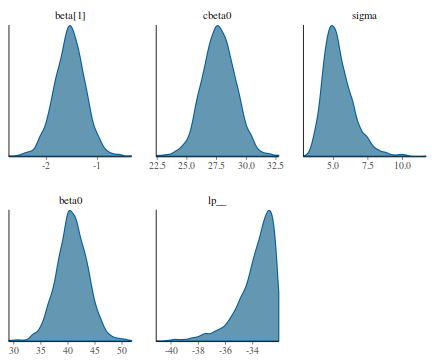
- Trace plots and density plots
- via shinystan
library(shinystan) launch_shinystan(data.rstan))
- It is worth exploring the influence of our priors.
Again, prior to examining the summaries, we should have explored the convergence diagnostics. There are numerous ways of working with STAN model fits (for exploring diagnostics and summarization).
- extract the mcmc samples and convert them into a mcmc.list to leverage the various coda routines
- use the numerous routines that come with the rstan package
- use the routines that come with the bayesplot package
- explore the diagnostics interactively via shinystan
- via coda
- Traceplots
- Autocorrelation
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.library(coda) s = as.array(data.rstanarm) mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(mcmc)
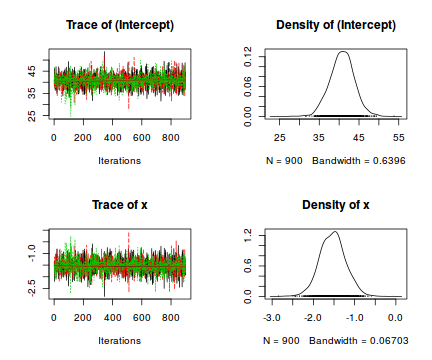 Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.library(coda) s = as.array(data.rstanarm) mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) autocorr.diag(mcmc)
(Intercept) x Lag 0 1.000000000 1.00000000 Lag 1 0.053211483 -0.02917861 Lag 5 0.004975124 0.01941260 Lag 10 -0.033296048 -0.04010251 Lag 50 -0.032866968 -0.01348437
- via rstan
- Traceplots
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
stan_trace(data.rstanarm)
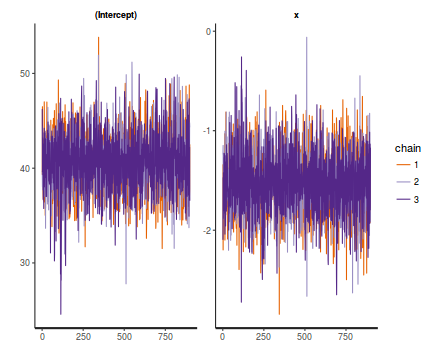
- Raftery diagnostic
The Raftery diagnostics for each chain estimate that we would require no more than 5000 samples to reach the specified level of confidence in convergence. As we have 16,667 samples, we can be confidence that convergence has occurred.
raftery.diag(data.rstanarm)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
- Autocorrelation diagnostic
A lag of 2 appears broadly sufficient to avoid autocorrelation (poor mixing).
stan_ac(data.rstanarm)
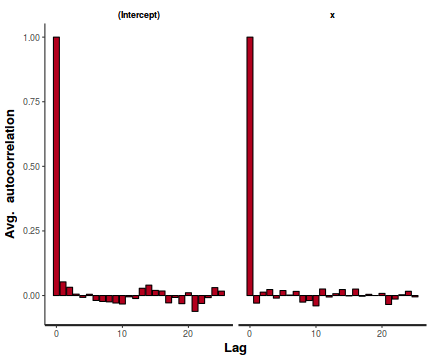
- Rhat values. These values are a measure of sampling efficiency/effectiveness. Ideally, all values should be less than 1.05.
If there are values of 1.05 or greater it suggests that the sampler was not very efficient or effective. Not only does this
mean that the sampler was potentiall slower than it could have been, more importantly, it could indicate that the sampler spent time sampling
in a region of the likelihood that is less informative. Such a situation can arise from either a misspecified model or
overly vague priors that permit sampling in otherwise nonscence parameter space.
In this instance, all rhat values are well below 1.05 (a good thing).
stan_rhat(data.rstanarm)
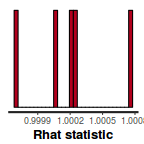
- Another measure of sampling efficiency is Effective Sample Size (ess).
ess indicate the number samples (or proportion of samples that the sampling algorithm deamed effective. The sampler rejects samples
on the basis of certain criterion and when it does so, the previous sample value is used. Hence while the MCMC sampling chain
may contain 1000 samples, if there are only 10 effective samples (1%), the estimated properties are not likely to be reliable.
In this instance, most of the parameters have reasonably high effective samples and thus there is likely to be a good range of values from which to estimate paramter properties.
stan_ess(data.rstanarm)
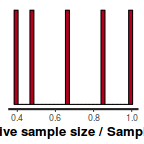
- Traceplots
- via bayesplot
- Trace plots and density plots
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
library(bayesplot) mcmc_trace(as.array(data.rstanarm), regex_pars = "Intercept|x|sigma")
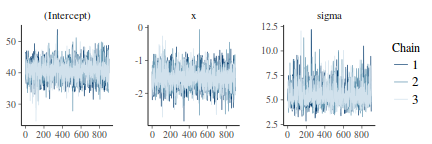
library(bayesplot) mcmc_combo(as.array(data.rstanarm))
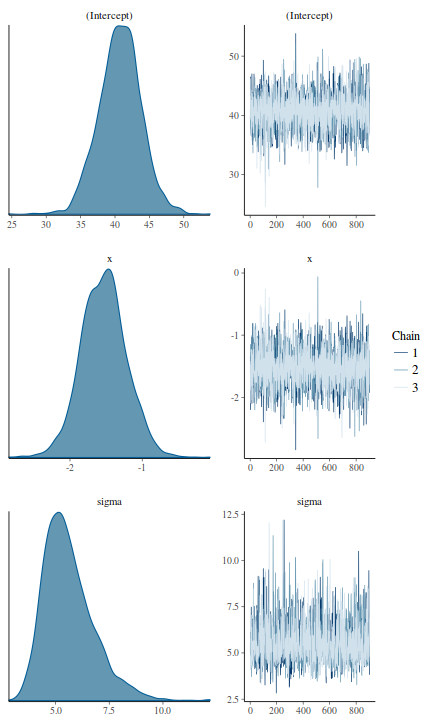
- Density plots
Density plots sugggest mean or median would be appropriate to describe the fixed posteriors and median is appropriate for the sigma posterior.
library(bayesplot) mcmc_dens(as.array(data.rstanarm))
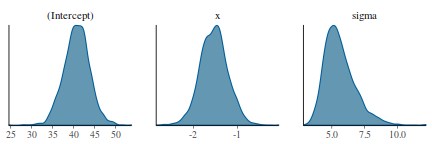
- Trace plots and density plots
- via rstanarm
The rstanarm package provides additional posterior checks.
- Posterior vs Prior - this compares the posterior estimate for each parameter against the associated prior.
If the spread of the priors is small relative to the posterior, then it is likely that the priors are too influential.
On the other hand, overly wide priors can lead to computational issues.
library(rstanarm) posterior_vs_prior(data.rstanarm, color_by = "vs", group_by = TRUE, facet_args = list(scales = "free_y"))
Gradient evaluation took 2.8e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.28 seconds. Adjust your expectations accordingly! Elapsed Time: 1.96278 seconds (Warm-up) 0.039246 seconds (Sampling) 2.00202 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 2.48823 seconds (Warm-up) 0.054196 seconds (Sampling) 2.54242 seconds (Total)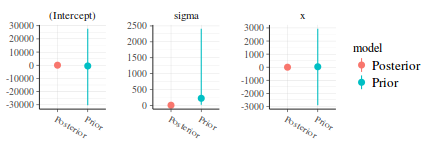
- Posterior vs Prior - this compares the posterior estimate for each parameter against the associated prior.
If the spread of the priors is small relative to the posterior, then it is likely that the priors are too influential.
On the other hand, overly wide priors can lead to computational issues.
- via shinystan
library(shinystan) launch_shinystan(data.rstanarm))
- It is worth exploring the influence of our priors.
Again, prior to examining the summaries, we should have explored the convergence diagnostics. There are numerous ways of working with STAN model fits (for exploring diagnostics and summarization).
- extract the mcmc samples and convert them into a mcmc.list to leverage the various coda routines
- use the numerous routines that come with the rstan package
- use the routines that come with the bayesplot package
- explore the diagnostics interactively via shinystan
- via coda
- Traceplots
- Autocorrelation
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.library(coda) mcmc = as.mcmc(data.brms) plot(mcmc)
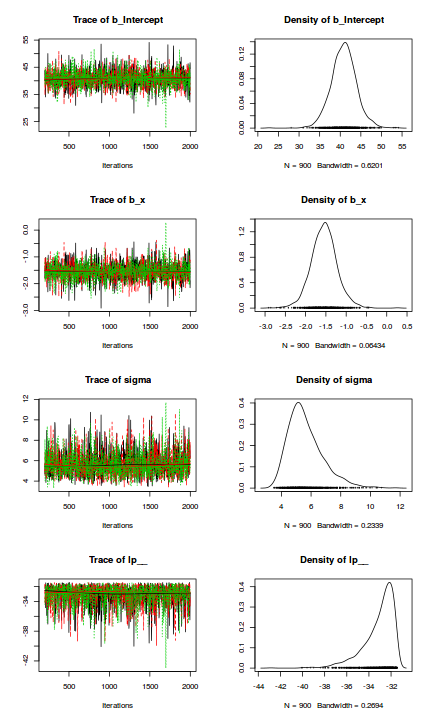 Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.library(coda) mcmc = as.mcmc(data.brms) autocorr.diag(mcmc)
Error in ts(x, start = start(x), end = end(x), deltat = thin(x)): invalid time series parameters specified
- via rstan
- Traceplots
Trace plots show no evidence that the chains have not reasonably traversed the entire multidimensional parameter space.
stan_trace(data.brms$fit)
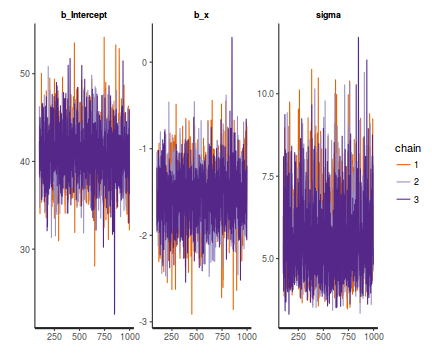
- Raftery diagnostic
The Raftery diagnostics for each chain estimate that we would require no more than 5000 samples to reach the specified level of confidence in convergence. As we have 16,667 samples, we can be confidence that convergence has occurred.
raftery.diag(data.brms)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
- Autocorrelation diagnostic
A lag of 2 appears broadly sufficient to avoid autocorrelation (poor mixing).
stan_ac(data.brms$fit)
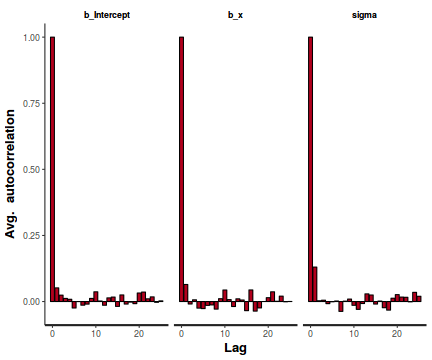
- Rhat values. These values are a measure of sampling efficiency/effectiveness. Ideally, all values should be less than 1.05.
If there are values of 1.05 or greater it suggests that the sampler was not very efficient or effective. Not only does this
mean that the sampler was potentiall slower than it could have been, more importantly, it could indicate that the sampler spent time sampling
in a region of the likelihood that is less informative. Such a situation can arise from either a misspecified model or
overly vague priors that permit sampling in otherwise nonscence parameter space.
In this instance, all rhat values are well below 1.05 (a good thing).
stan_rhat(data.brms$fit)
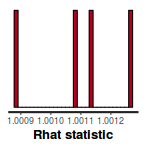
- Another measure of sampling efficiency is Effective Sample Size (ess).
ess indicate the number samples (or proportion of samples that the sampling algorithm deamed effective. The sampler rejects samples
on the basis of certain criterion and when it does so, the previous sample value is used. Hence while the MCMC sampling chain
may contain 1000 samples, if there are only 10 effective samples (1%), the estimated properties are not likely to be reliable.
In this instance, most of the parameters have reasonably high effective samples and thus there is likely to be a good range of values from which to estimate paramter properties.
stan_ess(data.brms$fit)
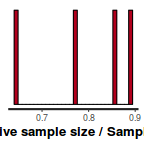
- Traceplots
Model validation
Model validation involves exploring the model diagnostics and fit to ensure that the model is broadly appropriate for the data. As such, exploration of the residuals should be routine.
For more complex models (those that contain multiple effects, it is also advisable to plot the residuals against each of the individual predictors. For sampling designs that involve sample collection over space or time, it is also a good idea to explore whether there are any temporal or spatial patterns in the residuals.
There are numerous situations (e.g. when applying specific variance-covariance structures to a model) where raw residuals do not reflect the interior workings of the model. Typically, this is because they do not take into account the variance-covariance matrix or assume a very simple variance-covariance matrix. Since the purpose of exploring residuals is to evaluate the model, for these cases, it is arguably better to draw conclusions based on standardized (or studentized) residuals.
Unfortunately the definitions of standardized and studentized residuals appears to vary and the two terms get used interchangeably. I will adopt the following definitions:
| Standardized residuals: | the raw residuals divided by the true standard deviation of the residuals (which of course is rarely known). | |
| Studentized residuals: | the raw residuals divided by the standard deviation of the residuals. Note that externally studentized residuals are calculated by dividing the raw residuals by a unique standard deviation for each observation that is calculated from regressions having left each successive observation out. | |
| Pearson residuals: | the raw residuals divided by the standard deviation of the response variable. |
The mark of a good model is being able to predict well. In an ideal world, we would have sufficiently large sample size as to permit us to hold a fraction (such as 25%) back thereby allowing us to train the model on 75% of the data and then see how well the model can predict the withheld 25%. Unfortunately, such a luxury is still rare in ecology.
The next best option is to see how well the model can predict the observed data. Models tend to struggle most with the extremes of trends and have particular issues when the extremes approach logical boundaries (such as zero for count data and standard deviations). We can use the fitted model to generate random predicted observations and then explore some properties of these compared to the actual observed data.
Residuals are not computed directly within MCMCpack. However, we can calculate them manually form the posteriors.
mcmc = as.data.frame(data.mcmcpack) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
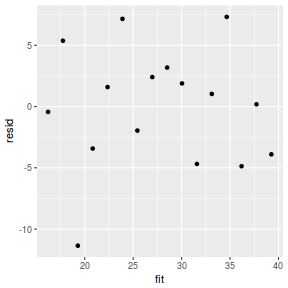
Residuals against predictors
mcmc = as.data.frame(data.mcmcpack) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = data$x))
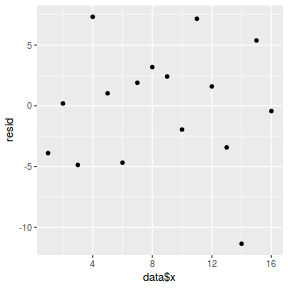
And now for studentized residuals
mcmc = as.data.frame(data.mcmcpack) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
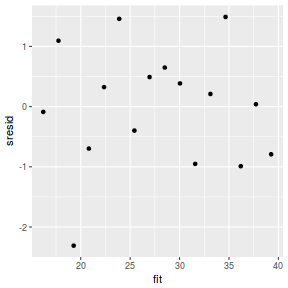
Conclusions: for this simple model, the studentized residuals yield the same pattern as the raw residuals (or the Pearson residuals for that matter).
Lets see how well data simulated from the model reflects the raw data
mcmc = as.matrix(data.mcmcpack) # generate a model matrix Xmat = model.matrix(~x, data) ## get median parameter estimates coefs = mcmc[, 1:2] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(mcmc), function(i) rnorm(nrow(data), fit[i, ], sqrt(mcmc[i, "sigma2"]))) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = data, aes(x = y, fill = "Obs"), alpha = 0.5)
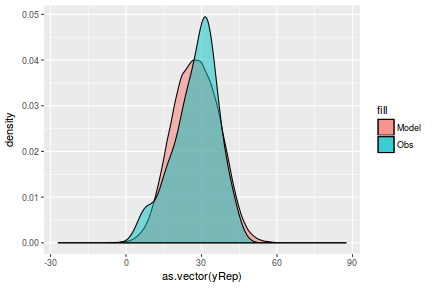
Although residuals can be computed directly within R2jags, we can calculate them manually from the posteriors to be consistent across other approaches.
mcmc = data.r2jags$BUGSoutput$sims.matrix[, c("beta0", "beta1")] # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
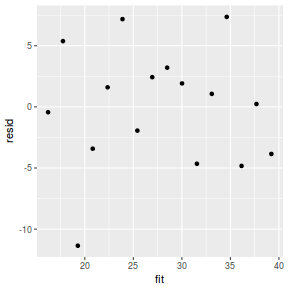
Residuals against predictors
mcmc = data.r2jags$BUGSoutput$sims.matrix[, c("beta0", "beta1")] # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = data$x))
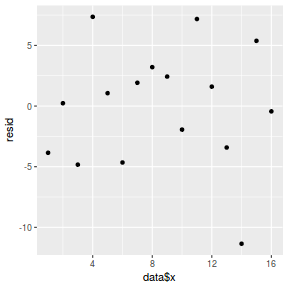
And now for studentized residuals
mcmc = data.r2jags$BUGSoutput$sims.matrix[, c("beta0", "beta1")] # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
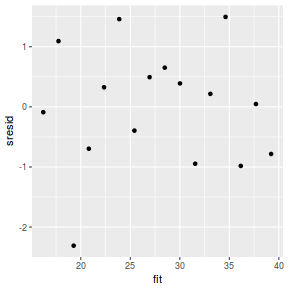
Conclusions: for this simple model, the studentized residuals yield the same pattern as the raw residuals (or the Pearson residuals for that matter).
Lets see how well data simulated from the model reflects the raw data
mcmc = data.r2jags$BUGSoutput$sims.matrix # generate a model matrix Xmat = model.matrix(~x, data) ## get median parameter estimates coefs = mcmc[, c("beta0", "beta1")] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(mcmc), function(i) rnorm(nrow(data), fit[i, ], mcmc[i, "sigma2"]))
Error in mcmc[i, "sigma2"]: subscript out of bounds
ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = data, aes(x = y, fill = "Obs"), alpha = 0.5)
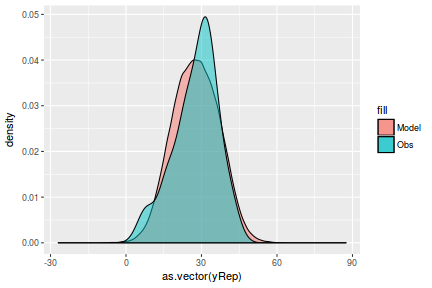
Although residuals can be computed directly within Rstan, we can calculate them manually from the posteriors to be consistent across other approaches.
mcmc = as.matrix(data.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
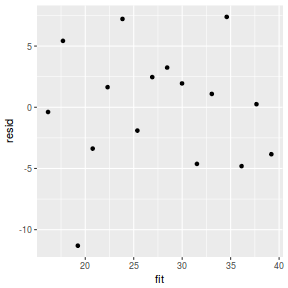
Residuals against predictors
mcmc = as.matrix(data.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = data$x))
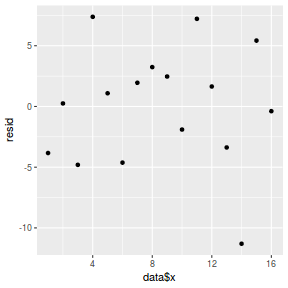
And now for studentized residuals
mcmc = as.matrix(data.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = apply(mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = data$y - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
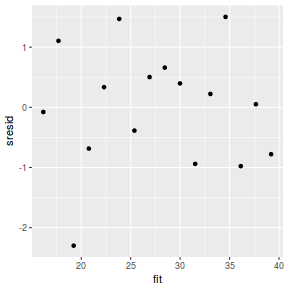
Conclusions: for this simple model, the studentized residuals yield the same pattern as the raw residuals (or the Pearson residuals for that matter).
Lets see how well data simulated from the model reflects the raw data
mcmc = as.matrix(data.rstan) # generate a model matrix Xmat = model.matrix(~x, data) ## get median parameter estimates coefs = mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(mcmc), function(i) rnorm(nrow(data), fit[i, ], mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = data, aes(x = y, fill = "Obs"), alpha = 0.5)
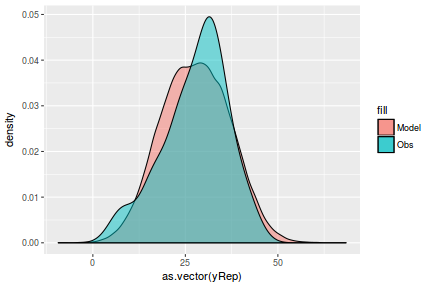
Residuals can be computed directly within RSTANARM.
resid = resid(data.rstanarm) fit = fitted(data.rstanarm) ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
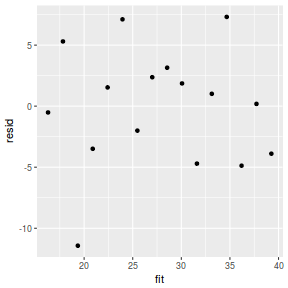
Residuals against predictors
resid = resid(data.rstanarm) fit = fitted(data.rstanarm) ggplot() + geom_point(data = NULL, aes(y = resid, x = data$x))
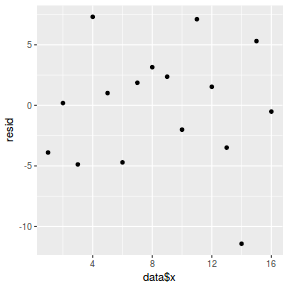
And now for studentized residuals
resid = resid(data.rstanarm) sresid = resid/sd(resid) fit = fitted(data.rstanarm) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
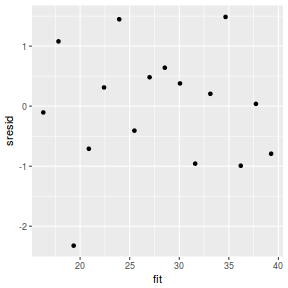
Conclusions: for this simple model, the studentized residuals yield the same pattern as the raw residuals (or the Pearson residuals for that matter).
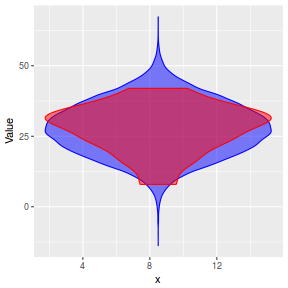
Lets compare draws (predictions) from the posterior (in blue) with the distributions of observed data (red) via violin plots. Violin plots are similar to boxplots except that they display more visual information about the density distribution.
y_pred = posterior_predict(data.rstanarm) newdata = data %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -y, -x) ggplot(newdata, aes(Value, x = x)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = data, aes(y = y, x = x), fill = "red", color = "red", alpha = 0.5)
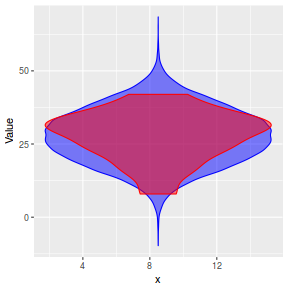
Yet another way to approach validation is to explore trends in posteriors in the context of the observed data.
## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) fit = posterior_predict(data.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = data, aes(y = y)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
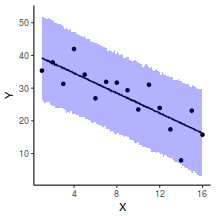
Conclusions the predicted trends do encapsulate the actual data, suggesting that the model is a reasonable representation of the underlying processes. Note, these are prediction intervals rather than confidence intervals as we are seeking intervals within which we can predict individual observations rather than means.
Residuals can be computed directly within BRMS. By default, the residuals and fitted extractor functions in brms return summarized versions (means, SE and credibility intervals). We are only interested in the mean (Estimate) estimates.
resid = resid(data.brms)[, "Estimate"] fit = fitted(data.brms)[, "Estimate"] ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
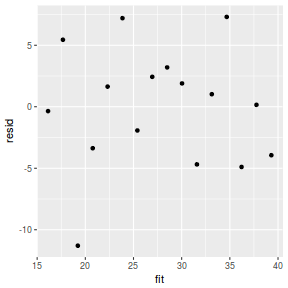
Residuals against predictors
resid = resid(data.brms)[, "Estimate"] fit = fitted(data.brms)[, "Estimate"] ggplot() + geom_point(data = NULL, aes(y = resid, x = data$x))
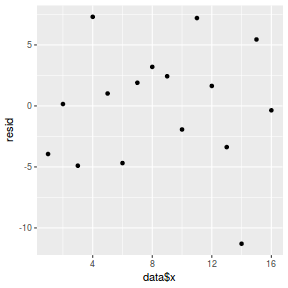
And now for studentized residuals
resid = resid(data.brms)[, "Estimate"] sresid = resid/sd(resid) fit = fitted(data.brms)[, "Estimate"] ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
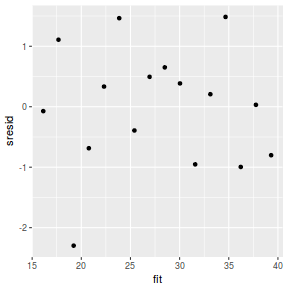
Conclusions: for this simple model, the studentized residuals yield the same pattern as the raw residuals (or the Pearson residuals for that matter).
Lets compare draws (predictions) from the posterior (in blue) with the distributions of observed data (red) via violin plots. Violin plots are similar to boxplots except that they display more visual information about the density distribution.
y_pred = posterior_predict(data.brms) newdata = data %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -y, -x) ggplot(newdata, aes(Value, x = x)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = data, aes(y = y, x = x), fill = "red", color = "red", alpha = 0.5)
Yet another way to approach validation is to explore trends in posteriors in the context of the observed data.
## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) fit = posterior_predict(data.brms, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = data, aes(y = y)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
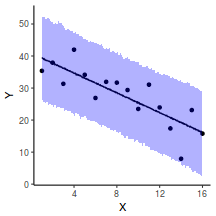
Conclusions the predicted trends do encapsulate the actual data, suggesting that the model is a reasonable representation of the underlying processes. Note, these are prediction intervals rather than confidence intervals as we are seeking intervals within which we can predict individual observations rather than means.
Notwithstanding the slight issue of autocorrelation in the sigma2 samples, there is no evidence that the mcmc chain did not converge on a stable posterior distribution. We are now in a position to examine the summaries of the parameters.
Parameter estimates (posterior summaries)
Although all parameters in a Bayesian analysis are considered random and are considered a distribution, rarely would it be useful to present tables of all the samples from each distribution. On the other hand, plots of the posterior distributions are do have some use. Nevertheless, most workers prefer to present simple statistical summaries of the posteriors. Popular choices include the median (or mean) and 95% credibility intervals.
summary(data.mcmcpack)
Iterations = 1001:11000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 10000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
(Intercept) 40.788 2.9157 0.029157 0.028679
x -1.538 0.3026 0.003026 0.003026
sigma2 30.453 14.0296 0.140296 0.162065
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
(Intercept) 35.087 38.949 40.802 42.620 46.6754
x -2.148 -1.729 -1.537 -1.349 -0.9395
sigma2 14.015 21.183 27.281 35.757 64.8614
# OR library(broom) tidyMCMC(data.mcmcpack, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 (Intercept) 40.787840 2.9156846 34.694040 46.2035365 2 x -1.538321 0.3026426 -2.133656 -0.9323802 3 sigma2 30.452600 14.0295572 10.955592 56.7338303
-1.5383211
change in y. That is, y declines at a rate of -1.5383211 per
unit increase in x.
The 95% confidence interval for the slope does not overlap with 0
implying a significant effect of x on y.
While workers attempt to become comfortable with a new statistical framework, it is only natural that they like to evaluate and comprehend new structures and output alongside more familiar concepts. One way to facilitate this is via Bayesian p-values that are somewhat analogous to the frequentist p-values for investigating the hypothesis that a parameter is equal to zero.
library(coda) mcmcpvalue <- function(samp) { ## elementary version that creates an empirical p-value for the ## hypothesis that the columns of samp have mean zero versus a general ## multivariate distribution with elliptical contours. ## differences from the mean standardized by the observed ## variance-covariance factor ## Note, I put in the bit for single terms if (length(dim(samp)) == 0) { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - mean(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/length(samp) } else { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - colMeans(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/nrow(samp) } } ## since values are less than zero mcmcpvalue(data.mcmcpack[, 2])
[1] 2e-04
With a p-value of essentially 0, we would conclude that there is almost no evidence that the slope was likely to be equal to zero, suggesting there is a relationship.
print(data.r2jags)
Inference for Bugs model at "../downloads/BUGSscripts/tut7.2bS4.1.txt", fit using jags,
3 chains, each with 53000 iterations (first 3000 discarded), n.thin = 10
n.sims = 15000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta0 40.776 3.012 34.771 38.854 40.754 42.700 46.732 1.001 6500
beta1 -1.536 0.309 -2.155 -1.739 -1.534 -1.339 -0.917 1.001 8800
sigma 5.612 1.198 3.825 4.765 5.433 6.244 8.454 1.001 15000
deviance 98.913 2.916 95.586 96.795 98.131 100.243 106.547 1.001 15000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 4.3 and DIC = 103.2
DIC is an estimate of expected predictive error (lower deviance is better).
# OR library(broom) tidyMCMC(as.mcmc(data.r2jags), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 beta0 40.776236 3.0118914 34.644637 46.5544619 2 beta1 -1.535883 0.3094887 -2.117052 -0.8847727 3 deviance 98.913094 2.9160662 95.342003 104.6398121 4 sigma 5.611529 1.1977617 3.510032 7.8862896
-1.535883
change in y. That is, y declines at a rate of -1.535883 per
unit increase in x.
The 95% confidence interval for the slope does not overlap with 0
implying a significant effect of x on y.
While workers attempt to become comfortable with a new statistical framework, it is only natural that they like to evaluate and comprehend new structures and output alongside more familiar concepts. One way to facilitate this is via Bayesian p-values that are somewhat analogous to the frequentist p-values for investigating the hypothesis that a parameter is equal to zero.
library(coda) mcmcpvalue <- function(samp) { ## elementary version that creates an empirical p-value for the ## hypothesis that the columns of samp have mean zero versus a general ## multivariate distribution with elliptical contours. ## differences from the mean standardized by the observed ## variance-covariance factor ## Note, I put in the bit for single terms if (length(dim(samp)) == 0) { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - mean(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/length(samp) } else { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - colMeans(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/nrow(samp) } } ## since values are less than zero mcmcpvalue(data.r2jags$BUGSoutput$sims.matrix[, c("beta1")])
[1] 0
With a p-value of essentially 0, we would conclude that there is almost no evidence that the slope was likely to be equal to zero, suggesting there is a relationship.
summary(data.rstan)
$summary
mean se_mean sd 2.5% 25% 50% 75% 97.5%
beta[1] -1.540077 0.005547721 0.2992531 -2.140083 -1.733530 -1.536049 -1.347254 -0.9578622
cbeta0 27.699678 0.026072380 1.4002154 24.952730 26.779818 27.686496 28.616701 30.4432020
sigma 5.378446 0.020515831 1.0852954 3.734084 4.614093 5.199031 5.958270 7.9476304
beta0 40.790336 0.053432423 2.9034858 35.075289 38.948498 40.737680 42.663585 46.4509997
lp__ -33.769878 0.026822294 1.3557193 -37.440064 -34.368897 -33.422015 -32.778343 -32.1970451
n_eff Rhat
beta[1] 2909.699 0.9994293
cbeta0 2884.220 1.0003349
sigma 2798.451 0.9995632
beta0 2952.770 0.9993640
lp__ 2554.746 0.9995627
$c_summary
, , chains = chain:1
stats
parameter mean sd 2.5% 25% 50% 75% 97.5%
beta[1] -1.531479 0.3068162 -2.109599 -1.735114 -1.539470 -1.334883 -0.9173666
cbeta0 27.746909 1.4159460 24.954516 26.855717 27.747541 28.659675 30.4723348
sigma 5.396365 1.0961031 3.734274 4.594885 5.232184 6.006155 7.8181447
beta0 40.764477 3.0140699 34.540731 38.900198 40.880995 42.739393 46.5386786
lp__ -33.809348 1.4068914 -37.550169 -34.393107 -33.462536 -32.782456 -32.1869446
, , chains = chain:2
stats
parameter mean sd 2.5% 25% 50% 75% 97.5%
beta[1] -1.550123 0.2974626 -2.155754 -1.746184 -1.538468 -1.353810 -1.010301
cbeta0 27.687988 1.3881674 25.134487 26.703722 27.683492 28.600342 30.383584
sigma 5.402310 1.0729273 3.838954 4.640805 5.209596 5.950922 7.982861
beta0 40.864033 2.8689516 35.483307 38.998427 40.801638 42.774958 46.193502
lp__ -33.734080 1.3104041 -37.188086 -34.291847 -33.386710 -32.790364 -32.213962
, , chains = chain:3
stats
parameter mean sd 2.5% 25% 50% 75% 97.5%
beta[1] -1.538631 0.2933243 -2.141996 -1.716454 -1.531518 -1.354423 -0.9678914
cbeta0 27.664137 1.3964915 24.918672 26.754701 27.613705 28.591730 30.4340678
sigma 5.336664 1.0866013 3.619856 4.595549 5.154616 5.908103 8.0011510
beta0 40.742497 2.8255388 35.183039 38.892966 40.634539 42.437613 46.3971867
lp__ -33.766205 1.3484235 -37.384673 -34.447354 -33.396535 -32.763341 -32.2065629
# OR library(broom) tidyMCMC(data.rstan, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 beta[1] -1.540077 0.2992531 -2.136075 -0.9571987 0.9994293 2910 2 cbeta0 27.699678 1.4002154 25.186804 30.6173088 1.0003349 2884 3 sigma 5.378446 1.0852954 3.487439 7.4980289 0.9995632 2798 4 beta0 40.790336 2.9034858 34.878535 46.2187799 0.9993640 2953
-1.5400774
change in y. That is, y declines at a rate of -1.5400774 per
unit increase in x.
The 95% confidence interval for the slope does not overlap with 0
implying a significant effect of x on y.
While workers attempt to become comfortable with a new statistical framework, it is only natural that they like to evaluate and comprehend new structures and output alongside more familiar concepts. One way to facilitate this is via Bayesian p-values that are somewhat analogous to the frequentist p-values for investigating the hypothesis that a parameter is equal to zero.
Also note that since our STAN model incorporated predictor centering, we have estimates of the intercept based on
both centered (cbeta0) and uncentered data (beta0). Since the intercept from uncentered data
is beyond the domain of our sampling data it has very little interpretability. However, the intercept based on centered
data can be interpreted as the estimate of the response at the mean predictor (in this case 27.699678).
library(coda) mcmcpvalue <- function(samp) { ## elementary version that creates an empirical p-value for the ## hypothesis that the columns of samp have mean zero versus a general ## multivariate distribution with elliptical contours. ## differences from the mean standardized by the observed ## variance-covariance factor ## Note, I put in the bit for single terms if (length(dim(samp)) == 0) { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - mean(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/length(samp) } else { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - colMeans(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/nrow(samp) } } ## since values are less than zero mcmcpvalue(as.matrix(data.rstan)[, c("beta[1]")])
[1] 0
With a p-value of essentially 0, we would conclude that there is almost no evidence that the slope was likely to be equal to zero, suggesting there is a relationship.
summary(data.rstanarm)
Model Info:
function: stan_glm
family: gaussian [identity]
formula: y ~ x
algorithm: sampling
priors: see help('prior_summary')
sample: 2700 (posterior sample size)
num obs: 16
Estimates:
mean sd 2.5% 25% 50% 75% 97.5%
(Intercept) 40.7 3.1 34.7 38.8 40.8 42.7 46.9
x -1.5 0.3 -2.2 -1.7 -1.5 -1.3 -0.9
sigma 5.6 1.2 3.8 4.8 5.4 6.2 8.5
mean_PPD 27.7 2.0 23.6 26.4 27.7 29.0 31.7
log-posterior -65.2 1.3 -68.6 -65.8 -64.9 -64.2 -63.7
Diagnostics:
mcse Rhat n_eff
(Intercept) 0.1 1.0 2271
x 0.0 1.0 2700
sigma 0.0 1.0 1264
mean_PPD 0.0 1.0 1808
log-posterior 0.0 1.0 1078
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).
# OR library(broom) tidyMCMC(data.rstanarm$stanfit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 (Intercept) 40.734015 3.0668570 34.412462 46.3425366 1.0000549 2271 2 x -1.531248 0.3148917 -2.123538 -0.8981083 1.0001968 2700 3 sigma 5.619764 1.1740461 3.604894 7.9675118 0.9996872 1264 4 mean_PPD 27.698236 2.0410524 23.858059 31.9079814 1.0002406 1808 5 log-posterior -65.225515 1.3374104 -67.797185 -63.5678144 1.0007470 1078
-1.5312483
change in y. That is, y declines at a rate of -1.5312483 per
unit increase in x.
The 95% confidence interval for the slope does not overlap with 0
implying a significant effect of x on y.
While workers attempt to become comfortable with a new statistical framework, it is only natural that they like to evaluate and comprehend new structures and output alongside more familiar concepts. One way to facilitate this is via Bayesian p-values that are somewhat analogous to the frequentist p-values for investigating the hypothesis that a parameter is equal to zero.
library(coda) mcmcpvalue <- function(samp) { ## elementary version that creates an empirical p-value for the ## hypothesis that the columns of samp have mean zero versus a general ## multivariate distribution with elliptical contours. ## differences from the mean standardized by the observed ## variance-covariance factor ## Note, I put in the bit for single terms if (length(dim(samp)) == 0) { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - mean(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/length(samp) } else { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - colMeans(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/nrow(samp) } } ## since values are less than zero mcmcpvalue(as.matrix(data.rstanarm)[, c("x")])
[1] 0
With a p-value of essentially 0, we would conclude that there is almost no evidence that the slope was likely to be equal to zero, suggesting there is a relationship.
Alternatively we can generate posterior intervals for each parameter.
posterior_interval(data.rstanarm, prob = 0.95)
2.5% 97.5% (Intercept) 34.668050 46.8721257 x -2.151347 -0.9122868 sigma 3.846747 8.4674463
An alternative way of quantifying the impact of a predictor is to compare models with and without
the predictor. In a Bayesian context, this can be achieved by comparing the leave-one-out
cross-validation statistics. Leave-one-out (LOO) cross-validation explores how well a series of models
can predict withheld values (Vehtari, Gelman, and Gabry, 2016b). The LOO Information Criterion (LOOIC) is analogous to the AIC except that
the LOOIC takes priors into consideration, does not assume that the posterior distribution is drawn from
a multivariate normal and integrates over parameter uncertainty so as to yield a distribution of looic
rather than just a point estimate. The LOOIC does however assume that all observations are equally
influential (it does not matter which observations are left out). This assumption can be examined via the
Pareta k estimate (values greater than 0.5 or more conservatively 0.75 are considered overly influential).
(full = loo(data.rstanarm))
Computed from 2700 by 16 log-likelihood matrix
Estimate SE
elpd_loo -51.2 3.2
p_loo 2.9 1.3
looic 102.4 6.3
Pareto k diagnostic values:
Count Pct
(-Inf, 0.5] (good) 15 93.8%
(0.5, 0.7] (ok) 1 6.2%
(0.7, 1] (bad) 0 0.0%
(1, Inf) (very bad) 0 0.0%
All Pareto k estimates are ok (k < 0.7)
See help('pareto-k-diagnostic') for details.
(reduced = loo(update(data.rstanarm, formula = . ~ 1)))
Gradient evaluation took 1.9e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.19 seconds.
Adjust your expectations accordingly!
Elapsed Time: 0.00911 seconds (Warm-up)
0.035428 seconds (Sampling)
0.044538 seconds (Total)
Gradient evaluation took 2e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.2 seconds.
Adjust your expectations accordingly!
Elapsed Time: 0.008509 seconds (Warm-up)
0.034266 seconds (Sampling)
0.042775 seconds (Total)
Gradient evaluation took 1.5e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds.
Adjust your expectations accordingly!
Elapsed Time: 0.011456 seconds (Warm-up)
0.035874 seconds (Sampling)
0.04733 seconds (Total)
Computed from 2700 by 16 log-likelihood matrix
Estimate SE
elpd_loo -59.4 3.1
p_loo 2.1 1.0
looic 118.8 6.2
Pareto k diagnostic values:
Count Pct
(-Inf, 0.5] (good) 15 93.8%
(0.5, 0.7] (ok) 0 0.0%
(0.7, 1] (bad) 1 6.2%
(1, Inf) (very bad) 0 0.0%
See help('pareto-k-diagnostic') for details.
par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
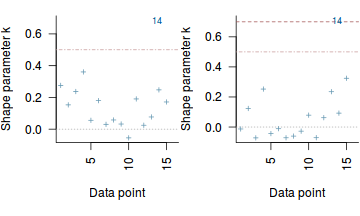
compare_models(full, reduced)
elpd_diff se
-8.2 1.8
summary(data.brms)
Family: gaussian(identity)
Formula: y ~ x
Data: data (Number of observations: 16)
Samples: 3 chains, each with iter = 2000; warmup = 200; thin = 2;
total post-warmup samples = 2700
ICs: LOO = Not computed; WAIC = Not computed
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
Intercept 40.85 3.07 34.90 47.24 2310 1
x -1.55 0.32 -2.18 -0.90 2408 1
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sigma 5.63 1.19 3.9 8.48 2091 1
Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
is a crude measure of effective sample size, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
# OR library(broom) tidyMCMC(data.brms$fit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 b_Intercept 40.853729 3.0714471 34.407211 46.6638946 1.001079 2310 2 b_x -1.545095 0.3205355 -2.141672 -0.8693169 1.001133 2408 3 sigma 5.631356 1.1888245 3.779939 8.2153548 1.001264 2091
-1.5450948
change in y. That is, y declines at a rate of -1.5450948 per
unit increase in x.
The 95% confidence interval for the slope does not overlap with 0
implying a significant effect of x on y.
Whilst workers attempt to become comfortable with a new statistical framework, it is only natural that they like to evaluate and comprehend new structures and output alongside more familiar concepts. One way to facilitate this is via Bayesian p-values that are somewhat analogous to the frequentist p-values for investigating the hypothesis that the two populations are identical (t=0).
library(coda) mcmcpvalue <- function(samp) { ## elementary version that creates an empirical p-value for the ## hypothesis that the columns of samp have mean zero versus a general ## multivariate distribution with elliptical contours. ## differences from the mean standardized by the observed ## variance-covariance factor ## Note, I put in the bit for single terms if (length(dim(samp)) == 0) { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - mean(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/length(samp) } else { std <- backsolve(chol(var(samp)), cbind(0, t(samp)) - colMeans(samp), transpose = TRUE) sqdist <- colSums(std * std) sum(sqdist[-1] > sqdist[1])/nrow(samp) } } ## since values are less than zero mcmcpvalue(as.matrix(data.brms)[, c("b_x")])
[1] 0.0007407407
With a p-value of essentially 0, we would conclude that there is almost no evidence that the slope was likely to be equal to zero, suggesting there is a relationship.
Alternatively we can generate posterior intervals for each parameter.
posterior_interval(as.matrix(data.brms), prob = 0.95)
2.5% 97.5% b_Intercept 34.899273 47.2408583 b_x -2.179970 -0.8959258 sigma 3.895194 8.4787733 lp__ -36.892779 -31.5536581
An alternative way of quantifying the impact of a predictor is to compare models with and without
the predictor. In a Bayesian context, this can be achieved by comparing the leave-one-out
cross-validation statistics. Leave-one-out (LOO) cross-validation explores how well a series of models
can predict withheld values (Vehtari, Gelman, and Gabry, 2016b). The LOO Information Criterion (LOOIC) is analogous to the AIC except that
the LOOIC takes priors into consideration, does not assume that the posterior distribution is drawn from
a multivariate normal and integrates over parameter uncertainty so as to yield a distribution of looic
rather than just a point estimate. The LOOIC does however assume that all observations are equally
influential (it does not matter which observations are left out). This assumption can be examined via the
Pareta k estimate (values greater than 0.5 or more conservatively 0.75 are considered overly influential).
(full = loo(data.brms))
LOOIC SE 102.43 6.22
(reduced = loo(update(data.brms, formula = . ~ 1)))
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1).
Gradient evaluation took 1.7e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 2000 [ 0%] (Warmup)
Iteration: 200 / 2000 [ 10%] (Warmup)
Iteration: 400 / 2000 [ 20%] (Warmup)
Iteration: 600 / 2000 [ 30%] (Warmup)
Iteration: 800 / 2000 [ 40%] (Warmup)
Iteration: 1000 / 2000 [ 50%] (Warmup)
Iteration: 1001 / 2000 [ 50%] (Sampling)
Iteration: 1200 / 2000 [ 60%] (Sampling)
Iteration: 1400 / 2000 [ 70%] (Sampling)
Iteration: 1600 / 2000 [ 80%] (Sampling)
Iteration: 1800 / 2000 [ 90%] (Sampling)
Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.022215 seconds (Warm-up)
0.029115 seconds (Sampling)
0.05133 seconds (Total)
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2).
Gradient evaluation took 1.9e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.19 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 2000 [ 0%] (Warmup)
Iteration: 200 / 2000 [ 10%] (Warmup)
Iteration: 400 / 2000 [ 20%] (Warmup)
Iteration: 600 / 2000 [ 30%] (Warmup)
Iteration: 800 / 2000 [ 40%] (Warmup)
Iteration: 1000 / 2000 [ 50%] (Warmup)
Iteration: 1001 / 2000 [ 50%] (Sampling)
Iteration: 1200 / 2000 [ 60%] (Sampling)
Iteration: 1400 / 2000 [ 70%] (Sampling)
Iteration: 1600 / 2000 [ 80%] (Sampling)
Iteration: 1800 / 2000 [ 90%] (Sampling)
Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.025044 seconds (Warm-up)
0.021075 seconds (Sampling)
0.046119 seconds (Total)
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3).
Gradient evaluation took 6e-06 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 2000 [ 0%] (Warmup)
Iteration: 200 / 2000 [ 10%] (Warmup)
Iteration: 400 / 2000 [ 20%] (Warmup)
Iteration: 600 / 2000 [ 30%] (Warmup)
Iteration: 800 / 2000 [ 40%] (Warmup)
Iteration: 1000 / 2000 [ 50%] (Warmup)
Iteration: 1001 / 2000 [ 50%] (Sampling)
Iteration: 1200 / 2000 [ 60%] (Sampling)
Iteration: 1400 / 2000 [ 70%] (Sampling)
Iteration: 1600 / 2000 [ 80%] (Sampling)
Iteration: 1800 / 2000 [ 90%] (Sampling)
Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.019155 seconds (Warm-up)
0.022313 seconds (Sampling)
0.041468 seconds (Total)
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1).
Gradient evaluation took 1.1e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 2000 [ 0%] (Warmup)
Iteration: 200 / 2000 [ 10%] (Warmup)
Iteration: 400 / 2000 [ 20%] (Warmup)
Iteration: 600 / 2000 [ 30%] (Warmup)
Iteration: 800 / 2000 [ 40%] (Warmup)
Iteration: 1000 / 2000 [ 50%] (Warmup)
Iteration: 1001 / 2000 [ 50%] (Sampling)
Iteration: 1200 / 2000 [ 60%] (Sampling)
Iteration: 1400 / 2000 [ 70%] (Sampling)
Iteration: 1600 / 2000 [ 80%] (Sampling)
Iteration: 1800 / 2000 [ 90%] (Sampling)
Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.012441 seconds (Warm-up)
0.018111 seconds (Sampling)
0.030552 seconds (Total)
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2).
Gradient evaluation took 3e-06 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 2000 [ 0%] (Warmup)
Iteration: 200 / 2000 [ 10%] (Warmup)
Iteration: 400 / 2000 [ 20%] (Warmup)
Iteration: 600 / 2000 [ 30%] (Warmup)
Iteration: 800 / 2000 [ 40%] (Warmup)
Iteration: 1000 / 2000 [ 50%] (Warmup)
Iteration: 1001 / 2000 [ 50%] (Sampling)
Iteration: 1200 / 2000 [ 60%] (Sampling)
Iteration: 1400 / 2000 [ 70%] (Sampling)
Iteration: 1600 / 2000 [ 80%] (Sampling)
Iteration: 1800 / 2000 [ 90%] (Sampling)
Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.012443 seconds (Warm-up)
0.016248 seconds (Sampling)
0.028691 seconds (Total)
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3).
Gradient evaluation took 1.6e-05 seconds
1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds.
Adjust your expectations accordingly!
Iteration: 1 / 2000 [ 0%] (Warmup)
Iteration: 200 / 2000 [ 10%] (Warmup)
Iteration: 400 / 2000 [ 20%] (Warmup)
Iteration: 600 / 2000 [ 30%] (Warmup)
Iteration: 800 / 2000 [ 40%] (Warmup)
Iteration: 1000 / 2000 [ 50%] (Warmup)
Iteration: 1001 / 2000 [ 50%] (Sampling)
Iteration: 1200 / 2000 [ 60%] (Sampling)
Iteration: 1400 / 2000 [ 70%] (Sampling)
Iteration: 1600 / 2000 [ 80%] (Sampling)
Iteration: 1800 / 2000 [ 90%] (Sampling)
Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 0.012169 seconds (Warm-up)
0.015697 seconds (Sampling)
0.027866 seconds (Total)
LOOIC SE 118.26 6.03
par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
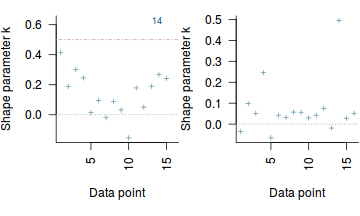
Graphical summaries
A nice graphic is often a great accompaniment to a statistical analysis. Although there are no fixed assumptions associated with graphing (in contrast to statistical analyses), we often want the graphical summaries to reflect the associated statistical analyses. After all, the sample is just one perspective on the population(s). What we are more interested in is being able to estimate and depict likely population parameters/trends.
Thus, whilst we could easily provide a plot displaying the raw data along with simple measures of location and spread, arguably, we should use estimates that reflect the fitted model. In this case, it would be appropriate to plot the credibility interval associated with each group.
mcmc = data.mcmcpack ## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) Xmat = model.matrix(~x, newdata) coefs = mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = x)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
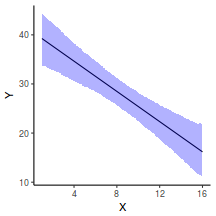
If you wanted to represent sample data on the figure in such a simple example (single predictor) we could simply over- (or under-) lay the raw data.
ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = data, aes(y = y, x = x), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
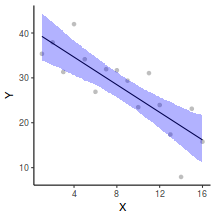
A more general solution would be to add the partial residuals to the figure. Partial residuals are the fitted values plus the residuals. In this simple case, that equates to exactly the same as the raw observations since $resid = obs - fitted$ and the fitted values depend only on the single predictor we are interested in.
## Calculate partial residuals fitted values fdata = rdata = data fMat = rMat = model.matrix(~x, fdata) fit = as.vector(apply(coefs, 2, median) %*% t(fMat)) resid = as.vector(data$y - apply(coefs, 2, median) %*% t(rMat)) rdata = rdata %>% mutate(partial.resid = resid + fit) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = rdata, aes(y = partial.resid), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
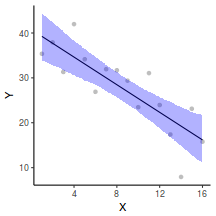
mcmc = data.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("beta0", "beta1")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = x)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
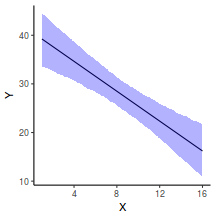
If you wanted to represent sample data on the figure in such a simple example (single predictor) we could simply over- (or under-) lay the raw data.
ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = data, aes(y = y, x = x), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
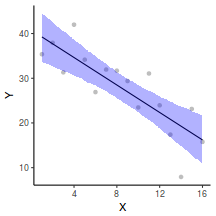
A more general solution would be to add the partial residuals to the figure. Partial residuals are the fitted values plus the residuals. In this simple case, that equates to exactly the same as the raw observations since $resid = obs - fitted $ and the fitted values depend only on the single predictor we are interested in.
## Calculate partial residuals fitted values fdata = rdata = data fMat = rMat = model.matrix(~x, fdata) fit = as.vector(apply(coefs, 2, median) %*% t(fMat)) resid = as.vector(data$y - apply(coefs, 2, median) %*% t(rMat)) rdata = rdata %>% mutate(partial.resid = resid + fit) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = rdata, aes(y = partial.resid), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
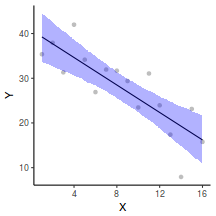
mcmc = as.matrix(data.rstan) ## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = x)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
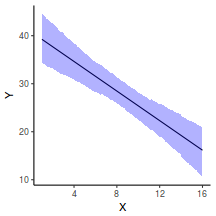
If you wanted to represent sample data on the figure in such a simple example (single predictor) we could simply over- (or under-) lay the raw data.
ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = data, aes(y = y, x = x), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
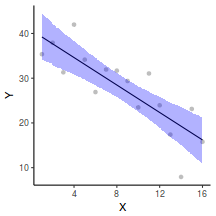
A more general solution would be to add the partial residuals to the figure. Partial residuals are the fitted values plus the residuals. In this simple case, that equates to exactly the same as the raw observations since $resid = obs - fitted $ and the fitted values depend only on the single predictor we are interested in.
## Calculate partial residuals fitted values fdata = rdata = data fMat = rMat = model.matrix(~x, fdata) fit = as.vector(apply(coefs, 2, median) %*% t(fMat)) resid = as.vector(data$y - apply(coefs, 2, median) %*% t(rMat)) rdata = rdata %>% mutate(partial.resid = resid + fit) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = rdata, aes(y = partial.resid), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
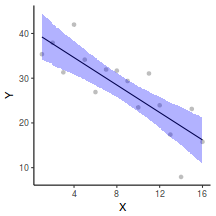
Although we could calculated the fitted values via matrix multiplication of the coefficients and the model matrix (as for MCMCpack, RJAGS and RSTAN), for more complex models, it is more convenient to use the posterior_linpred function that comes with rstantools.
## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) # fit = posterior_predict(data.rstanarm, newdata=newdata) fit = posterior_linpred(data.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = x)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
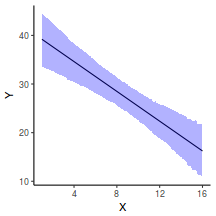
If you wanted to represent sample data on the figure in such a simple example (single predictor) we could simply over- (or under-) lay the raw data.
ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = data, aes(y = y, x = x), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
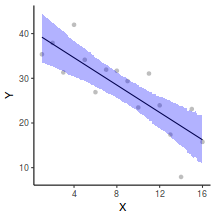
A more general solution would be to add the partial residuals to the figure. Partial residuals are the fitted values plus the residuals. In this simple case, that equates to exactly the same as the raw observations since $resid = obs - fitted $ and the fitted values depend only on the single predictor we are interested in.
## Calculate partial residuals fitted values fdata = rdata = data pp = posterior_predict(data.rstanarm, newdata = fdata) fit = as.vector(apply(pp, 2, median)) pp = posterior_predict(data.rstanarm, newdata = rdata) resid = as.vector(data$y - apply(pp, 2, median)) rdata = rdata %>% mutate(partial.resid = resid + fit) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = rdata, aes(y = partial.resid), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
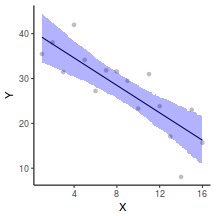
Although we could calculated the fitted values via matrix multiplication of the coefficients and the model matrix (as for MCMCpack, RJAGS and RSTAN), for more complex models, it is more convenient to use the marginal_effects function that comes with brms.
plot(marginal_effects(data.brms), points = TRUE)
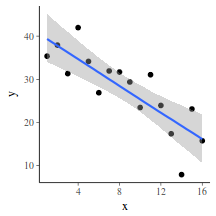
It is also possible to just use the marginal_effects function to generate the partial effects data which can then be plotted manually. Just note the names of the columns produced...
newdata = marginal_effects(data.brms)$x newdata %>% head
x y cond__ estimate__ se__ lower__ upper__ 1 1.000000 NA 1 39.33572 2.555412 33.98311 45.12585 2 1.151515 NA 1 39.10511 2.518356 33.85225 44.80221 3 1.303030 NA 1 38.86400 2.479195 33.69083 44.46928 4 1.454545 NA 1 38.62627 2.446745 33.54161 44.15459 5 1.606061 NA 1 38.39589 2.400776 33.37734 43.84009 6 1.757576 NA 1 38.17167 2.362441 33.21209 43.50193
ggplot(newdata, aes(y = estimate__, x = x)) + geom_line() + geom_ribbon(aes(ymin = lower__, ymax = upper__), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
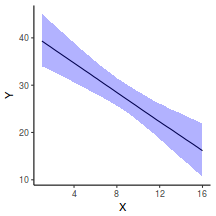
If you wanted to represent sample data on the figure in such a simple example (single predictor) we could simply over- (or under-) lay the raw data.
ggplot(newdata, aes(y = estimate__, x = x)) + geom_point(data = data, aes(y = y, x = x), color = "gray") + geom_line() + geom_ribbon(aes(ymin = lower__, ymax = upper__), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
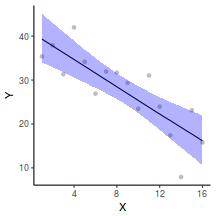
A more general solution would be to add the partial residuals to the figure. Partial residuals are the fitted values plus the residuals. In this simple case, that equates to exactly the same as the raw observations since $resid = obs - fitted $ and the fitted values depend only on the single predictor we are interested in.
mcmc = as.matrix(data.brms) ## Calculate the fitted values newdata = data.frame(x = seq(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE), len = 1000)) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("b_Intercept", "b_x")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ## Calculate partial residuals fitted values fdata = rdata = data fMat = rMat = model.matrix(~x, fdata) fit = as.vector(apply(coefs, 2, median) %*% t(fMat)) resid = as.vector(data$y - apply(coefs, 2, median) %*% t(rMat)) rdata = rdata %>% mutate(partial.resid = resid + fit) ggplot(newdata, aes(y = estimate, x = x)) + geom_point(data = rdata, aes(y = partial.resid), color = "gray") + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Y") + scale_x_continuous("X") + theme_classic()
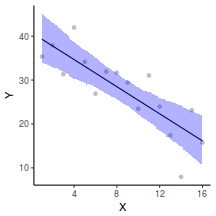
Effect sizes
In addition to deriving the distribution means for the slope parameter, we could make use of the Bayesian framework to derive the distribution of the effect size. In so doing, effect size could be considered as either the rate of change or alternatively, the difference between pairs of values along the predictor gradient. For the latter case, there are multiple ways of calculating an effect size, but the two most common are:
- Raw effect size
- the difference between two groups (as already calculated)
- Cohen's D
- the effect size standardized by division with the pooled standard deviation $$ D = (\mu_A - \mu_B)/\sigma $$
- Percent effect size
- expressing the effect size as a percent of one of the pairs. That is, whether you expressing a percentage increase or a percentage decline depends on which of the pairs of values are considered a reference value. Care must be exercised to ensure no division by zeros occur.
For simple linear models, effect size based on a rate is essentially the same as above except that it is expressed per unit of the predictor. Of course in many instances, one unit change in the predictor represents too subtle a shift in the underlying gradient to likely yield any ecologically meaningful or appreciable change in response.
Lets explore a range of effect sizes:
- Raw effect size between the largest and smallest x
- Cohen's D
- Percentage change between the largest and smallest x
- Fractional change between the largest and smallest x
Probability that a change in x is associated with greater than a 25% decline in y. Clearly, in order to explore this inference, we must first express the change in y as a percentage. This in turn requires us to calculate start and end points from which to calculate the magnitude of the effect (amount of decline in y) as well as the percentage decline. Hence, we start by predicting the distribution of y at the lowest and highest values of x.
mcmc = data.mcmcpack newdata = data.frame(x = c(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE))) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("(Intercept)", "x")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -23.07482 4.53964 -32.00484 -13.9857
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/sqrt(mcmc[, "sigma2"]) (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -4.43846 1.168116 -6.752846 -2.21918
# Percentage change (relative to Group A) ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -58.38874 8.549874 -75.0835 -41.3122
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9986
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.4161556 0.08539488 0.24904 0.5865297
Conclusions:
- On average, Y declines by
-23.074816over the observed range of x. We are 95% confident that the decline is between-32.0048416and-13.9857023. - The Cohen's D associated with a change over the observed range of x is
-4.4384597. - On average, Y declines by
-58.389%over the observed range of x. We are 95% confident that the decline is between-75.084%and-41.312%. - The probability that Y declines by more than 25% over the observed range of x is
0.999. - On average, Y declines by a factor of
0.416%over the observed range of x. We are 95% confident that the decline is between a factor of0.249%and0.587%.
Lets explore a range of effect sizes:
- Raw effect size between the largest and smallest x
- Cohen's D
- Percentage change between the largest and smallest x
- Fractional change between the largest and smallest x
Probability that a change in x is associated with greater than a 25% decline in y. Clearly, in order to explore this inference, we must first express the change in y as a percentage. This in turn requires us to calculate start and end points from which to calculate the magnitude of the effect (amount of decline in y) as well as the percentage decline. Hence, we start by predicting the distribution of y at the lowest and highest values of x.
mcmc = data.r2jags$BUGSoutput$sims.matrix newdata = data.frame(x = c(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE))) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("beta0", "beta1")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -23.03824 4.64233 -31.75579 -13.27159
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -4.276647 1.166878 -6.610581 -2.039906
# Percentage change (relative to Group A) ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -58.28882 8.755287 -75.37096 -40.51335
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9982
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.4171118 0.08755287 0.2462904 0.5948665
Conclusions:
- On average, Y declines by
-23.0382448over the observed range of x. We are 95% confident that the decline is between-31.7557852and-13.2715912. - The Cohen's D associated with a change over the observed range of x is
-4.2766474. - On average, Y declines by
-58.289%over the observed range of x. We are 95% confident that the decline is between-75.371%and-40.513%. - The probability that Y declines by more than 25% over the observed range of x is
0.998. - On average, Y declines by a factor of
0.417%over the observed range of x. We are 95% confident that the decline is between a factor of0.246%and0.595%.
Lets explore a range of effect sizes:
- Raw effect size between the largest and smallest x
- Cohen's D
- Percentage change between the largest and smallest x
- Fractional change between the largest and smallest x
Probability that a change in x is associated with greater than a 25% decline in y. Clearly, in order to explore this inference, we must first express the change in y as a percentage. This in turn requires us to calculate start and end points from which to calculate the magnitude of the effect (amount of decline in y) as well as the percentage decline. Hence, we start by predicting the distribution of y at the lowest and highest values of x.
mcmc = as.matrix(data.rstan) newdata = data.frame(x = c(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE))) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -23.10116 4.488796 -32.04112 -14.35798
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -4.453289 1.150329 -6.766335 -2.289957
# Percentage change (relative to Group A) ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -58.46377 8.445858 -75.83271 -42.96449
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9993333
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.4153623 0.08445858 0.2416729 0.5703551
Conclusions:
- On average, Y declines by
-23.101161over the observed range of x. We are 95% confident that the decline is between-32.0411213and-14.3579804. - The Cohen's D associated with a change over the observed range of x is
-4.4532885. - On average, Y declines by
-58.464%over the observed range of x. We are 95% confident that the decline is between-75.833%and-42.964%. - The probability that Y declines by more than 25% over the observed range of x is
0.999. - On average, Y declines by a factor of
0.415%over the observed range of x. We are 95% confident that the decline is between a factor of0.242%and0.570%.
Lets explore a range of effect sizes:
- Raw effect size between the largest and smallest x
- Cohen's D
- Percentage change between the largest and smallest x
- Fractional change between the largest and smallest x
Probability that a change in x is associated with greater than a 25% decline in y. Clearly, in order to explore this inference, we must first express the change in y as a percentage. This in turn requires us to calculate start and end points from which to calculate the magnitude of the effect (amount of decline in y) as well as the percentage decline. Hence, we start by predicting the distribution of y at the lowest and highest values of x.
mcmc = as.matrix(data.rstanarm) newdata = data.frame(x = c(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE))) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("(Intercept)", "x")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -22.96872 4.723375 -31.85307 -13.47162
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -4.252559 1.16655 -6.533503 -2.049772
# Percentage change (relative to Group A) ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -58.14203 8.945745 -74.70909 -39.84752
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9985185
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.4185797 0.08945745 0.2529091 0.6015248
Conclusions:
- On average, Y declines by
-22.9687244over the observed range of x. We are 95% confident that the decline is between-31.8530656and-13.4716247. - The Cohen's D associated with a change over the observed range of x is
-4.2525591. - On average, Y declines by
-58.142%over the observed range of x. We are 95% confident that the decline is between-74.709%and-39.848%. - The probability that Y declines by more than 25% over the observed range of x is
0.999. - On average, Y declines by a factor of
0.419%over the observed range of x. We are 95% confident that the decline is between a factor of0.253%and0.602%.
Lets explore a range of effect sizes:
- Raw effect size between the largest and smallest x
- Cohen's D
- Percentage change between the largest and smallest x
- Fractional change between the largest and smallest x
Probability that a change in x is associated with greater than a 25% decline in y. Clearly, in order to explore this inference, we must first express the change in y as a percentage. This in turn requires us to calculate start and end points from which to calculate the magnitude of the effect (amount of decline in y) as well as the percentage decline. Hence, we start by predicting the distribution of y at the lowest and highest values of x.
mcmc = as.matrix(data.brms) newdata = data.frame(x = c(min(data$x, na.rm = TRUE), max(data$x, na.rm = TRUE))) Xmat = model.matrix(~x, newdata) coefs = mcmc[, c("b_Intercept", "b_x")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -23.17642 4.808033 -32.12509 -13.03975
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -4.28766 1.176568 -6.596148 -1.951322
# Percentage change (relative to Group A) ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -58.50167 9.213223 -75.36007 -39.18994
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9966667
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.4149833 0.09213223 0.2463993 0.6081006
Conclusions:
- On average, Y declines by
-23.1764222over the observed range of x. We are 95% confident that the decline is between-32.125086and-13.0397529. - The Cohen's D associated with a change over the observed range of x is
-4.2876597. - On average, Y declines by
-58.502%over the observed range of x. We are 95% confident that the decline is between-75.360%and-39.190%. - The probability that Y declines by more than 25% over the observed range of x is
0.997. - On average, Y declines by a factor of
0.415%over the observed range of x. We are 95% confident that the decline is between a factor of0.246%and0.608%.
Posteriors
Finite Population Standard Deviations
Variance components, the amount of added variance attributed to each influence, are traditionally estimated for so called random effects. These are the effects for which the levels employed in the design are randomly selected to represent a broader range of possible levels. For such effects, effect sizes (differences between each level and a reference level) are of little value. Instead, the 'importance' of the variables are measured in units of variance components.
On the other hand, regular variance components for fixed factors (those whose measured levels represent the only levels of interest) are not logical - since variance components estimate variance as if the levels are randomly selected from a larger population. Nevertheless, in order to compare and contrast the scale of variability of both fixed and random factors, it is necessary to measure both on the same scale (sample or population based variance).
Finite-population variance components (Gelman, 2005) assume that the levels of all
factors (fixed and random) in the design are all the possible levels available.
In other words, they are assumed to represent finite populations of levels.
Sample (rather than population) statistics are then used to calculate these
finite-population variances (or standard deviations).
Since standard deviation (and variance) are bound at zero, standard deviation posteriors are typically non-normal. Consequently, medians and HPD intervals are more robust estimates.
library(broom) mcmc = data.mcmcpack sd.x = abs(mcmc[, "x"]) * sd(data$x) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = mcmc[, 1:2] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 7.324011 1.4401645 4.439017 10.158235 2 sd.resid 5.113917 0.3125066 4.916653 5.689996
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 59.81066 5.410107 48.00330 64.16565 2 sd.resid 40.18934 5.410107 35.83435 51.99670
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
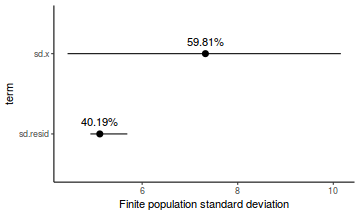
Conclusions:
Approximately 59.8%
of the total finite population standard deviation is due to x.
library(broom) mcmc = data.r2jags$BUGSoutput$sims.matrix sd.x = abs(mcmc[, "beta1"]) * sd(data$x) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = mcmc[, 1:2] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 7.312266 1.4734608 4.212361 10.079185 2 sd.resid 5.123532 0.3064685 4.916653 5.728441
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 59.76241 5.634456 47.19196 64.16565 2 sd.resid 40.23759 5.634456 35.83435 52.80804
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
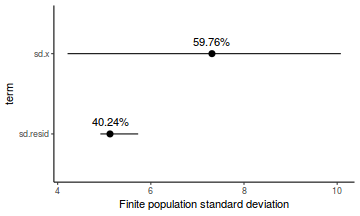
Conclusions:
Approximately 59.8%
of the total finite population standard deviation is due to x.
library(broom) mcmc = as.matrix(data.rstan) sd.x = abs(mcmc[, "beta[1]"]) * sd(data$x) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 7.332235 1.4247297 4.557177 10.169750 2 sd.resid 5.110913 0.2865312 4.916653 5.666491
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 59.79741 5.318334 48.03619 64.16563 2 sd.resid 40.20259 5.318334 35.83437 51.96381
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
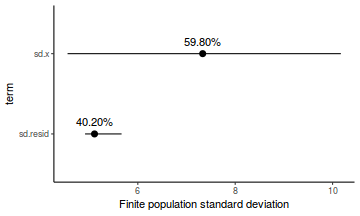
Conclusions:
Approximately 59.8%
of the total finite population standard deviation is due to x.
library(broom) mcmc = as.matrix(data.rstanarm) sd.x = abs(mcmc[, "x"]) * sd(data$x) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = mcmc[, 1:2] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 7.290200 1.4991843 4.275851 10.110062 2 sd.resid 5.130423 0.3148904 4.916653 5.738437
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 59.72643 5.864832 46.65895 64.16561 2 sd.resid 40.27357 5.864832 35.83439 53.34105
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
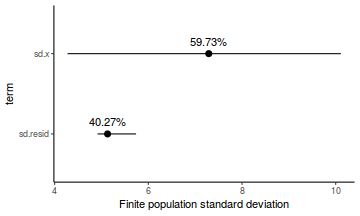
Conclusions:
Approximately 59.7%
of the total finite population standard deviation is due to x.
library(broom) mcmc = as.matrix(data.brms) sd.x = abs(mcmc[, "b_x"]) * sd(data$x) # generate a model matrix newdata = data.frame(x = data$x) Xmat = model.matrix(~x, newdata) ## get median parameter estimates coefs = mcmc[, 1:2] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 7.357990 1.5170233 4.138776 10.196400 2 sd.resid 5.135858 0.3567607 4.916653 5.786968
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 59.88833 5.89935 46.88813 64.16558 2 sd.resid 40.11167 5.89935 35.83442 53.11187
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
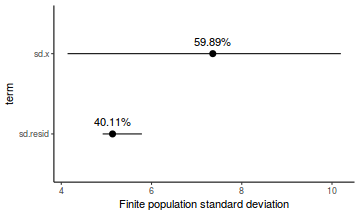
Conclusions:
Approximately 59.9%
of the total finite population standard deviation is due to x.
$R^2$
In a frequentist context, the $R^2$ value is seen as a useful indicator of goodness of fit. Whilst it has long been acknowledged that this measure is not appropriate for comparing models (for such purposes information criterion such as AIC are more appropriate), it is nevertheless useful for estimating the amount (percent) of variance explained by the model.
In a frequentist context, $R^2$ is calculated as the variance in predicted values divided by the variance in the observed (response) values.
Unfortunately, this classical formulation does not translate simply into a Bayesian context since
the equivalently calculated numerator can be larger than the an equivalently calculated denominator - thereby resulting in an $R^2$
greater than 100%. Gelman, Goodrich, Gabry, and Ali (2017) proposed an alternative
formulation in which the denominator comprises the sum of the explained variance and the variance of the residuals.
So in the standard regression model notation of: $$ \begin{align} y_i \sim{}& N(\mu_i, \sigma)\\ \mu_i =& \mathbf{X}\boldsymbol{\beta} \end{align} $$ The $R^2$ could be formulated as: $$ R^2 = \frac{\sigma^2_f}{\sigma^2_f + \sigma^2_e} $$ where $\sigma^2_f = var(\mu)$, ($\mu = \mathbf{X}\boldsymbol{\beta})$) and for Gaussian models $\sigma^2_e = var(y-\mu)$
library(broom) mcmc <- data.mcmcpack Xmat = model.matrix(~x, data) coefs = mcmc[, c("(Intercept)", "x")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.6596643 0.09983966 0.4601296 0.7622622
# for comparison with frequentist summary(lm(y ~ x, data))
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-11.3455 -3.5205 0.6545 2.6319 7.3650
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40.747 2.669 15.268 4.03e-10 ***
x -1.534 0.276 -5.558 7.06e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.089 on 14 degrees of freedom
Multiple R-squared: 0.6881, Adjusted R-squared: 0.6658
F-statistic: 30.89 on 1 and 14 DF, p-value: 7.057e-05
library(broom) mcmc <- data.r2jags$BUGSoutput$sims.matrix Xmat = model.matrix(~x, data) coefs = mcmc[, c("beta0", "beta1")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.6573356 0.1040998 0.4440158 0.7622622
# for comparison with frequentist summary(lm(y ~ x, data))
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-11.3455 -3.5205 0.6545 2.6319 7.3650
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40.747 2.669 15.268 4.03e-10 ***
x -1.534 0.276 -5.558 7.06e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.089 on 14 degrees of freedom
Multiple R-squared: 0.6881, Adjusted R-squared: 0.6658
F-statistic: 30.89 on 1 and 14 DF, p-value: 7.057e-05
library(broom) mcmc <- as.matrix(data.rstan) Xmat = model.matrix(~x, data) coefs = mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.6604948 0.098497 0.4607843 0.7622619
# for comparison with frequentist summary(lm(y ~ x, data))
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-11.3455 -3.5205 0.6545 2.6319 7.3650
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40.747 2.669 15.268 4.03e-10 ***
x -1.534 0.276 -5.558 7.06e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.089 on 14 degrees of freedom
Multiple R-squared: 0.6881, Adjusted R-squared: 0.6658
F-statistic: 30.89 on 1 and 14 DF, p-value: 7.057e-05
library(broom) mcmc <- as.matrix(data.rstanarm) Xmat = model.matrix(~x, data) coefs = mcmc[, c("(Intercept)", "x")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.6548455 0.107712 0.433476 0.7622615
# for comparison with frequentist summary(lm(y ~ x, data))
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-11.3455 -3.5205 0.6545 2.6319 7.3650
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40.747 2.669 15.268 4.03e-10 ***
x -1.534 0.276 -5.558 7.06e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.089 on 14 degrees of freedom
Multiple R-squared: 0.6881, Adjusted R-squared: 0.6658
F-statistic: 30.89 on 1 and 14 DF, p-value: 7.057e-05
library(broom) mcmc <- as.matrix(data.brms) Xmat = model.matrix(~x, data) coefs = mcmc[, c("b_Intercept", "b_x")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, data$y, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.6588937 0.107873 0.4380028 0.7622611
# for comparison with frequentist summary(lm(y ~ x, data))
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-11.3455 -3.5205 0.6545 2.6319 7.3650
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 40.747 2.669 15.268 4.03e-10 ***
x -1.534 0.276 -5.558 7.06e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.089 on 14 degrees of freedom
Multiple R-squared: 0.6881, Adjusted R-squared: 0.6658
F-statistic: 30.89 on 1 and 14 DF, p-value: 7.057e-05
References
Gelman, A. (2005). “Analysis of Variance - Why it is More Important Than Ever”. In: The Annals of Statistics 33.1, pp. 1–53.
Gelman, A., B. Goodrich, J. Gabry, et al. (2017). “R-squared for Bayesian regression models”.
Gelman, A. and J. Hill (2007). Data Analysis Using Regression and Multilevel/hierarchical Models. Cambridge, UK: Cambridge University Press.
Kery, M. (2010). Introduction to WinBUGS for Ecologists: Bayesian approach to regression, ANOVA, mixed models and related analyses. 1st ed. Academic Press. ISBN: 0123786053. URL: http://www.amazon.com/exec/obidos/redirect?tag=citeulike07-20\&path=ASIN/0123786053.
Logan, M. (2010). Biostatistical Design and Analysis Using R, a practical guide. Wiley-Blackwell.
McCarthy, M. A. (2007). Bayesian methods for ecology. Cambridge, Massachusetts: Cambridge University Press. ISBN: 0521615593. URL: http://www.amazon.com/exec/obidos/redirect?tag=citeulike07-20\&path=ASIN/0521615593.
Quinn, G. P. and K. J. Keough (2002). Experimental design and data analysis for biologists. London: Cambridge University Press.
Vehtari, A, A. Gelman and J. Gabry (2016b). “Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC”. In: Statistics and Computing.
Worked Examples
Simple linear regression
Here is an example from Fowler, Cohen and Parvis (1998). An agriculturalist was interested in the effects of fertilizer load on the yield of grass. Grass seed was sown uniformly over an area and different quantities of commercial fertilizer were applied to each of ten 1 m2 randomly located plots. Two months later the grass from each plot was harvested, dried and weighed. The data are in the file fertilizer.csv.
Download Fertilizer data set| Format of fertilizer.csv data files | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||
Open the fertilizer dataset
fert <- read.table("../downloads/data/fertilizer.csv", header = T, sep = ",", strip.white = T) fert
FERTILIZER YIELD 1 25 84 2 50 80 3 75 90 4 100 154 5 125 148 6 150 169 7 175 206 8 200 244 9 225 212 10 250 248
-
The artificial researchers were most likely interested in investigating whether there was a relationship between grass yield and fertilizer concentration.
Write out an appropriate linear model.
-
Perform exploratory data analysis to help guide what sort of analysis will be suitable
and whether the various assumptions are likely to be met.
Show code
ggplot(fert, aes(y = YIELD, x = FERTILIZER)) + geom_point()
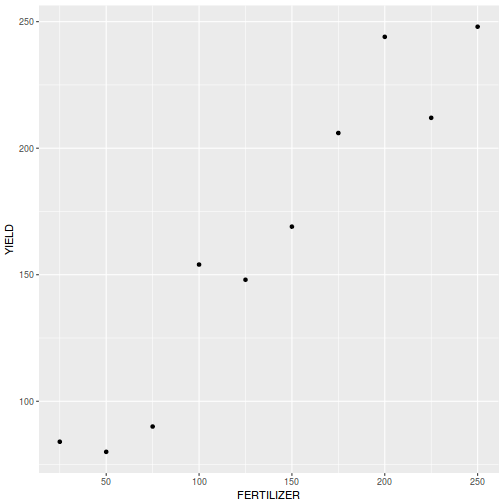
ggplot(fert, aes(y = YIELD, x = 1)) + geom_boxplot()
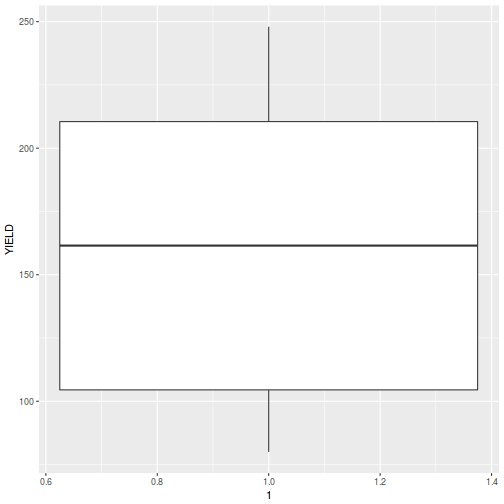
-
Fit the appropriate Bayesian model.
Show MCMCpack code
library(MCMCpack) fert.mcmcpack = MCMCregress(YIELD ~ FERTILIZER, data = fert)
Show JAGS codemodelString=" model { #Likelihood for (i in 1:n) { yield[i]~dnorm(mu[i],tau) mu[i] <- alpha+beta*fertilizer[i] } #Priors alpha ~ dnorm (0.01,1.0E-6) beta ~ dnorm(0,1.0E-6) tau <- 1 / (sigma * sigma) sigma~dgamma(0.001,0.001) } " ## write the model to a text file (I suggest you alter the path to somewhere more relevant ## to your system!) writeLines(modelString,con="../downloads/BUGSscripts/tut7.2bQ1_JAGS.txt") fert.list <- with(fert, list(fertilizer=FERTILIZER, yield=YIELD,n=nrow(fert)) ) #inits <- rep(list(list(alpha=mean(fert$YIELD), beta=0, # sigma=sd(fert$YIELD))),3) params <- c("alpha","beta","sigma") burnInSteps = 2000 nChains = 3 numSavedSteps = 50000 thinSteps = 10 nIter = ceiling((numSavedSteps * thinSteps)/nChains) fert.r2jags <- jags(data=fert.list, inits=NULL, #or inits=list(inits,inits,inits) # since there are three chains parameters.to.save=params, model.file="../downloads/BUGSscripts/tut7.2bQ1_JAGS.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph information: Observed stochastic nodes: 10 Unobserved stochastic nodes: 3 Total graph size: 53 Initializing model
Show RSTAN codemodelString = " data { int<lower=1> n; // total number of observations vector[n] Y; // response variable int<lower=1> nX; // number of effects matrix[n, nX] X; // model matrix } ransformed data { matrix[n, nX - 1] Xc; // centered version of X vector[nX - 1] means_X; // column means of X before centering for (i in 2:nX) { means_X[i - 1] = mean(X[, i]); Xc[, i - 1] = X[, i] - means_X[i - 1]; } } parameters { vector[nX-1] beta; // population-level effects real cbeta0; // center-scale intercept real<lower=0> sigma; // residual SD } ransformed parameters { } model { vector[n] mu; mu = Xc * beta + cbeta0; // prior specifications beta ~ normal(0, 100); cbeta0 ~ normal(0, 100); sigma ~ cauchy(0, 5); // likelihood contribution Y ~ normal(mu, sigma); } generated quantities { real beta0; // population-level intercept beta0 = cbeta0 - dot_product(means_X, beta); } " Xmat <- model.matrix(~FERTILIZER, data = fert) fert.list <- with(fert, list(Y = YIELD, X = Xmat, nX = ncol(Xmat), n = nrow(fert))) library(rstan) fert.rstan <- stan(data = fert.list, model_code = modelString, chains = 3, iter = 5000, warmup = 500, thin = 2)
In file included from /usr/local/lib/R/site-library/BH/include/boost/config.hpp:39:0, from /usr/local/lib/R/site-library/BH/include/boost/math/tools/config.hpp:13, from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/core/var.hpp:7, from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/core/gevv_vvv_vari.hpp:5, from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/core.hpp:12, from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/rev/mat.hpp:4, from /usr/local/lib/R/site-library/StanHeaders/include/stan/math.hpp:4, from /usr/local/lib/R/site-library/StanHeaders/include/src/stan/model/model_header.hpp:4, from file39d3243970d.cpp:8: /usr/local/lib/R/site-library/BH/include/boost/config/compiler/gcc.hpp:186:0: warning: "BOOST_NO_CXX11_RVALUE_REFERENCES" redefined # define BOOST_NO_CXX11_RVALUE_REFERENCES ^ <command-line>:0:0: note: this is the location of the previous definition SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 1). Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.019704 seconds (Warm-up) 0.059723 seconds (Sampling) 0.079427 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 2). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.012823 seconds (Warm-up) 0.062457 seconds (Sampling) 0.07528 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 3). Gradient evaluation took 1.5e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.018759 seconds (Warm-up) 0.07513 seconds (Sampling) 0.093889 seconds (Total)Show RSTANARM codefert.rstanarm = stan_glm(YIELD ~ FERTILIZER, data = fert, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior_intercept = normal(0, 1000), prior = normal(0, 1000), prior_aux = cauchy(0, 25))
Gradient evaluation took 1.7e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds. Adjust your expectations accordingly! Elapsed Time: 2.87974 seconds (Warm-up) 1.8448 seconds (Sampling) 4.72454 seconds (Total) Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Elapsed Time: 1.88517 seconds (Warm-up) 1.45586 seconds (Sampling) 3.34103 seconds (Total) Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Elapsed Time: 2.30701 seconds (Warm-up) 1.26275 seconds (Sampling) 3.56975 seconds (Total)Show BRMS codefert.brm = brm(YIELD ~ FERTILIZER, data = fert, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior = c(prior(normal(0, 1000), class = "Intercept"), prior(normal(0, 1000), class = "b"), prior(cauchy(0, 25), class = "sigma")))
Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Elapsed Time: 0.019368 seconds (Warm-up) 0.085001 seconds (Sampling) 0.104369 seconds (Total) Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Elapsed Time: 0.018599 seconds (Warm-up) 0.062118 seconds (Sampling) 0.080717 seconds (Total) Gradient evaluation took 6e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds. Adjust your expectations accordingly! Elapsed Time: 0.018222 seconds (Warm-up) 0.063125 seconds (Sampling) 0.081347 seconds (Total) - Explore MCMC diagnostics
Show MCMCpack code
library(MCMCpack) plot(fert.mcmcpack)
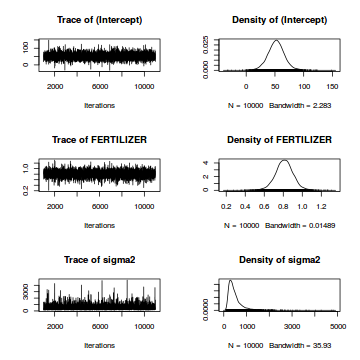
raftery.diag(fert.mcmcpack)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) (Intercept) 3 4267 3746 1.140 FERTILIZER 3 4129 3746 1.100 sigma2 2 3680 3746 0.982autocorr.diag(fert.mcmcpack)
(Intercept) FERTILIZER sigma2 Lag 0 1.000000000 1.0000000000 1.0000000000 Lag 1 -0.004037621 -0.0114692120 0.2554797754 Lag 5 -0.004986237 0.0054805924 0.0092656838 Lag 10 -0.012538601 -0.0161207640 0.0009712328 Lag 50 -0.001201054 -0.0005511779 0.0037849556
Show JAGS codelibrary(R2jags) library(coda) fert.mcmc = as.mcmc(fert.r2jags) plot(fert.mcmc)
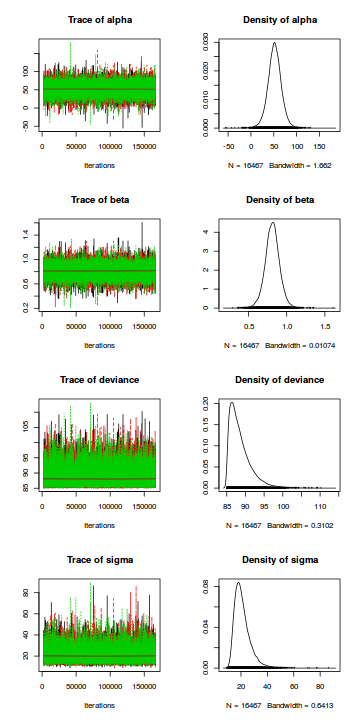
raftery.diag(fert.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 36350 3746 9.70 beta 20 38210 3746 10.20 deviance 20 38020 3746 10.10 sigma 20 37270 3746 9.95 [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 38020 3746 10.10 beta 10 37440 3746 9.99 deviance 20 37640 3746 10.00 sigma 20 37830 3746 10.10 [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 37080 3746 9.90 beta 10 37440 3746 9.99 deviance 20 37830 3746 10.10 sigma 20 37000 3746 9.88autocorr.diag(fert.mcmc)
alpha beta deviance sigma Lag 0 1.0000000000 1.0000000000 1.000000000 1.000000000 Lag 10 -0.0044127316 -0.0023406056 0.004963650 0.015916804 Lag 50 -0.0060828419 -0.0028847071 0.004949708 -0.001727307 Lag 100 0.0057039932 0.0030810054 -0.005268254 0.002371374 Lag 500 -0.0005423204 -0.0008620483 0.010255930 0.008363875
Show RSTAN codelibrary(rstan) library(coda) s = as.array(fert.rstan) fert.mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(fert.mcmc)
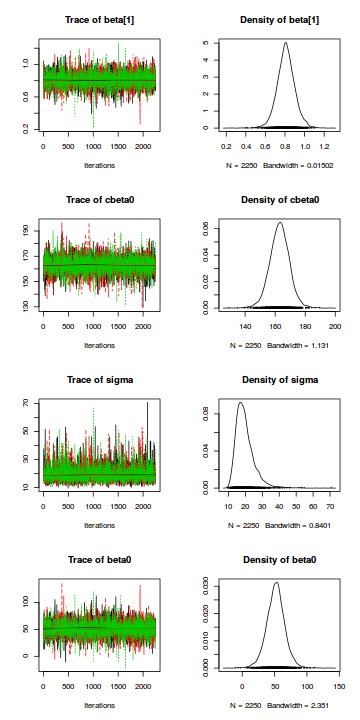
raftery.diag(fert.mcmc)
$`1` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`2` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`3` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(fert.mcmc)
beta[1] cbeta0 sigma beta0 Lag 0 1.000000000 1.00000000 1.0000000000 1.000000000 Lag 1 0.059317207 0.07926084 0.1737320913 0.068192640 Lag 5 -0.001646535 0.01350466 0.0209769999 -0.011735998 Lag 10 -0.011774603 0.01984983 0.0006350554 -0.001634785 Lag 50 -0.008110674 0.02465931 -0.0189181231 0.009131390
library(rstan) library(coda) stan_ac(fert.rstan)
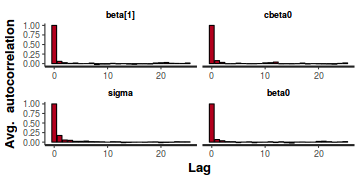
stan_rhat(fert.rstan)
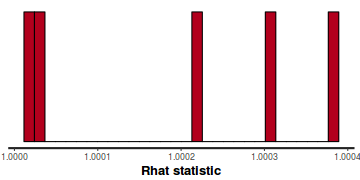
stan_ess(fert.rstan)
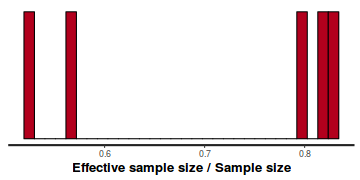
# using Bayeseplot library(bayesplot) detach("package:reshape") mcmc_trace(as.array(fert.rstan))
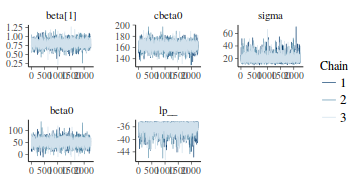
mcmc_trace(as.array(fert.rstan), regex_pars = "beta|sigma")
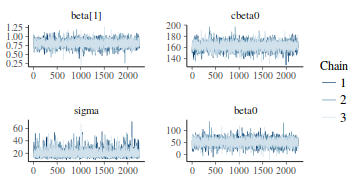
mcmc_dens(as.array(fert.rstan))
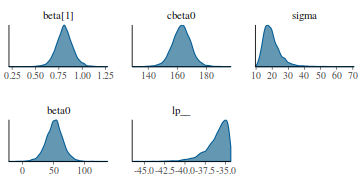
detach("package:reshape") library(bayesplot) mcmc_combo(as.array(fert.rstan))
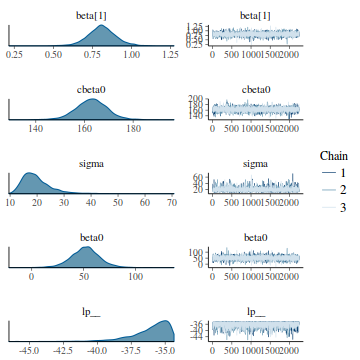 Show RSTANARM code
Show RSTANARM codelibrary(rstan) library(coda) s = as.array(fert.rstanarm) fert.mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(fert.mcmc)
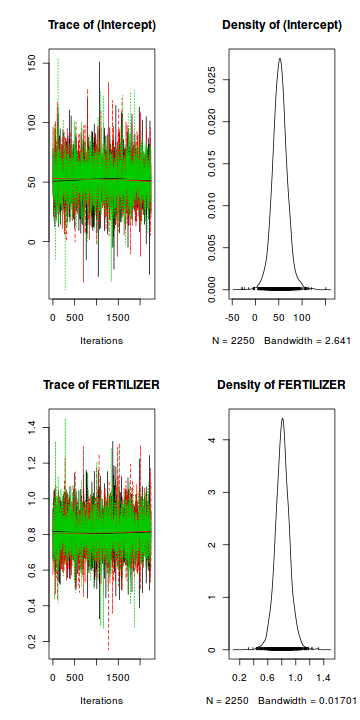
raftery.diag(fert.mcmc)
$`1` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`2` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`3` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(fert.mcmc)
(Intercept) FERTILIZER Lag 0 1.000000e+00 1.000000e+00 Lag 1 9.245402e-02 2.710592e-02 Lag 5 2.809036e-03 8.528322e-03 Lag 10 -2.278203e-03 -6.860284e-05 Lag 50 -5.866553e-05 -6.178508e-03
library(rstan) library(coda) stan_ac(fert.rstanarm)
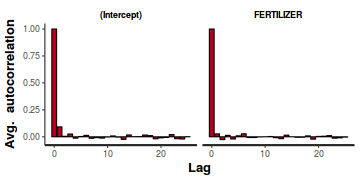
stan_rhat(fert.rstanarm)
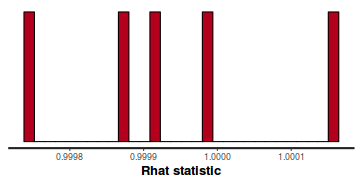
stan_ess(fert.rstanarm)
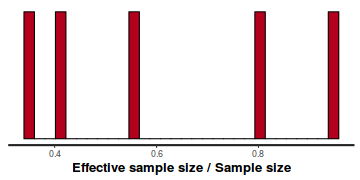
# using Bayeseplot library(bayesplot) detach("package:reshape") mcmc_trace(as.array(fert.rstanarm))
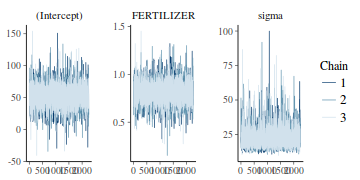
mcmc_trace(as.array(fert.rstanarm), regex_pars = "Intercept|FERT|sigma")
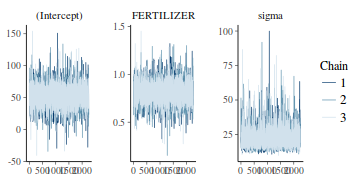
mcmc_dens(as.array(fert.rstanarm))
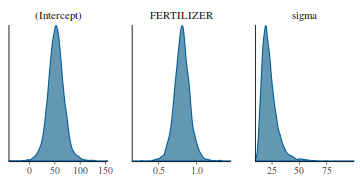
detach("package:reshape") library(bayesplot) mcmc_combo(as.array(fert.rstanarm))
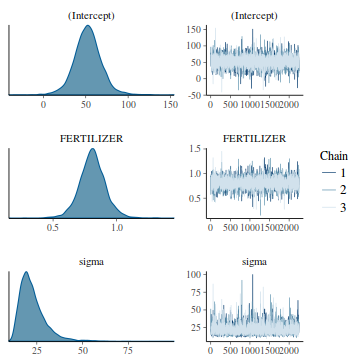
library(rstanarm) posterior_vs_prior(fert.rstanarm, color_by = "vs", group_by = TRUE, facet_args = list(scales = "free_y"))
Gradient evaluation took 2.5e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.25 seconds. Adjust your expectations accordingly! Elapsed Time: 2.7357 seconds (Warm-up) 0.034422 seconds (Sampling) 2.77012 seconds (Total) Gradient evaluation took 1.2e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds. Adjust your expectations accordingly! Elapsed Time: 3.71385 seconds (Warm-up) 0.031524 seconds (Sampling) 3.74537 seconds (Total)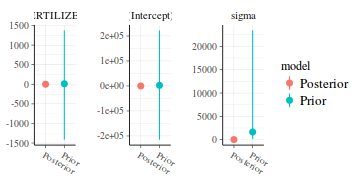 Show BRMS code
Show BRMS codelibrary(coda) library(brms) fert.mcmc = as.mcmc(fert.brm) plot(fert.mcmc)
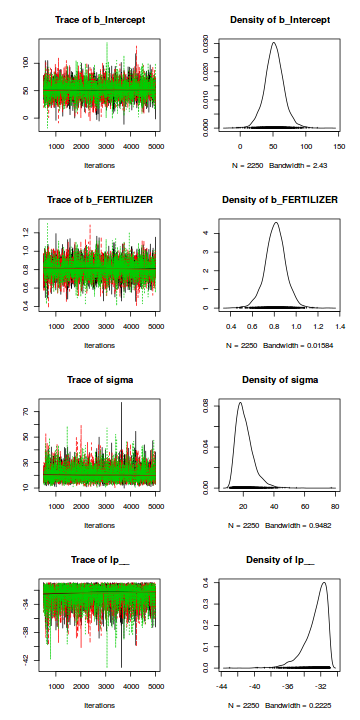
raftery.diag(fert.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(fert.mcmc)
Error in ts(x, start = start(x), end = end(x), deltat = thin(x)): invalid time series parameters specified
library(coda) stan_ac(fert.brm$fit)
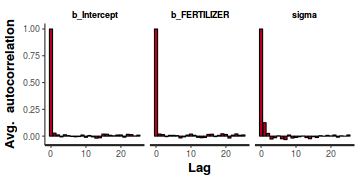
stan_rhat(fert.brm$fit)
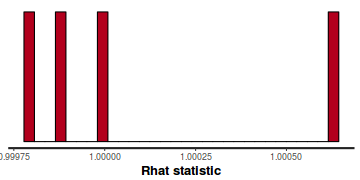
stan_ess(fert.brm$fit)
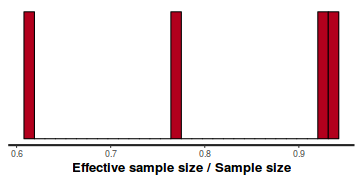
- Perform model validation
Show MCMCpack code
library(MCMCpack) fert.mcmc = as.data.frame(fert.mcmcpack) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = apply(fert.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = fert$YIELD - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
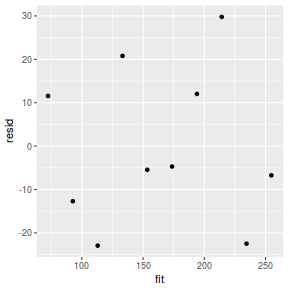
library(MCMCpack) fert.mcmc = as.data.frame(fert.mcmcpack) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = apply(fert.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = fert$YIELD - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fert$FERTILIZER))
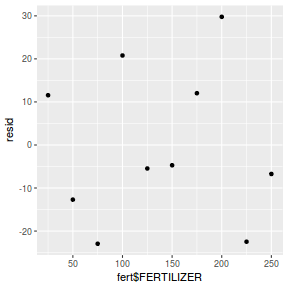
library(MCMCpack) fert.mcmc = as.data.frame(fert.mcmcpack) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = apply(fert.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = fert$YIELD - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
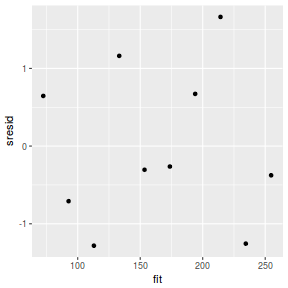
library(MCMCpack) fert.mcmc = as.matrix(fert.mcmcpack) # generate a model matrix Xmat = model.matrix(~FERTILIZER, fert) ## get median parameter estimates coefs = fert.mcmc[, 1:2] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(fert.mcmc), function(i) rnorm(nrow(fert), fit[i, ], sqrt(fert.mcmc[i, "sigma2"]))) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = fert, aes(x = YIELD, fill = "Obs"), alpha = 0.5)
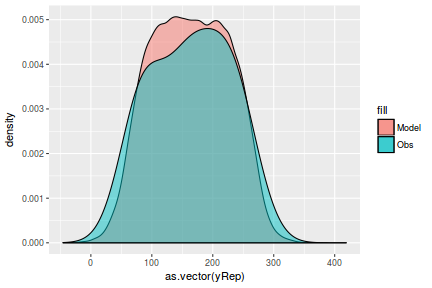 Show JAGS code
Show JAGS codelibrary(R2jags) fert.mcmc = fert.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = apply(fert.mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = fert$YIELD - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
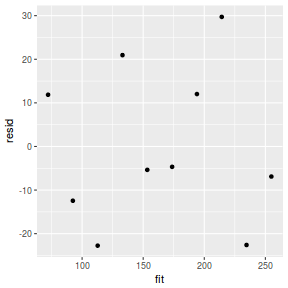
ggplot() + geom_point(data = NULL, aes(y = resid, x = fert$FERTILIZER))
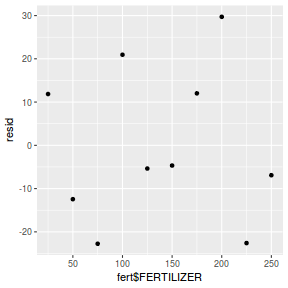
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
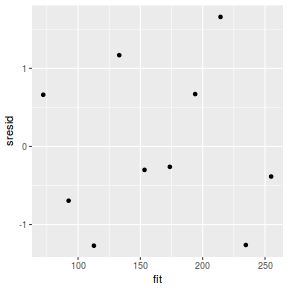
fert.mcmc = fert.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta", "sigma")] # generate a model matrix Xmat = model.matrix(~FERTILIZER, fert) ## get median parameter estimates coefs = fert.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(fert.mcmc), function(i) rnorm(nrow(fert), fit[i, ], fert.mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = fert, aes(x = YIELD, fill = "Obs"), alpha = 0.5)
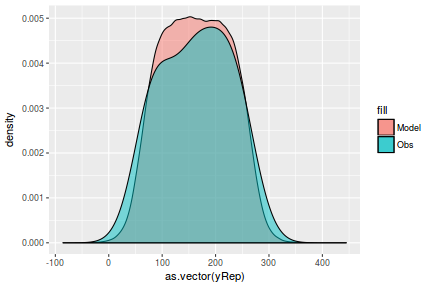 Show RSTAN code
Show RSTAN codelibrary(rstan) fert.mcmc = as.matrix(fert.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = apply(fert.mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = fert$YIELD - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
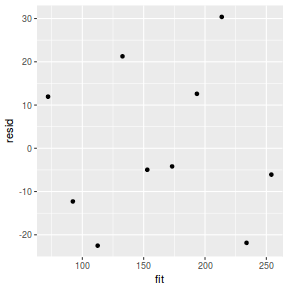
ggplot() + geom_point(data = NULL, aes(y = resid, x = fert$FERTILIZER))
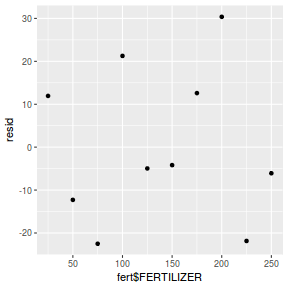
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
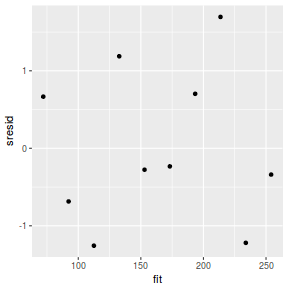
fert.mcmc = as.matrix(fert.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix Xmat = model.matrix(~FERTILIZER, fert) ## get median parameter estimates coefs = fert.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(fert.mcmc), function(i) rnorm(nrow(fert), fit[i, ], fert.mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = fert, aes(x = YIELD, fill = "Obs"), alpha = 0.5)
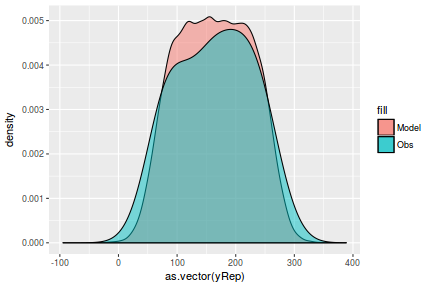 Show RSTANARM code
Show RSTANARM codelibrary(rstanarm) resid = resid(fert.rstanarm) fit = fitted(fert.rstanarm) ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
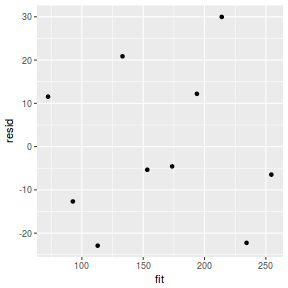
ggplot() + geom_point(data = NULL, aes(y = resid, x = fert$FERTILIZER))
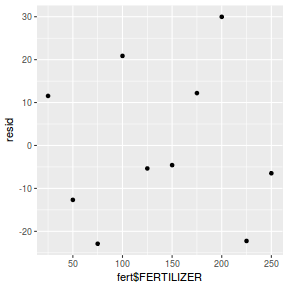
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
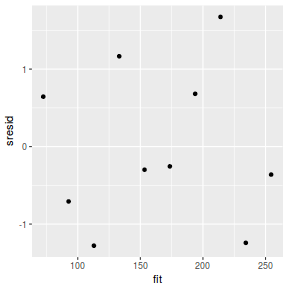
y_pred = posterior_predict(fert.rstanarm) newdata = fert %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -YIELD, -FERTILIZER) ggplot(newdata, aes(Value, x = FERTILIZER)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = fert, aes(y = YIELD, x = FERTILIZER), fill = "red", color = "red", alpha = 0.5)
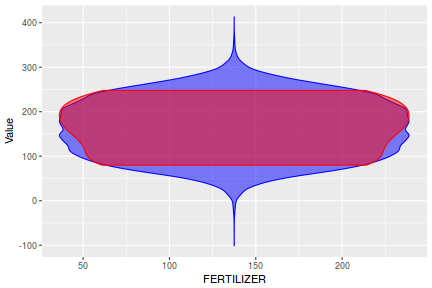
## Calculate the fitted values newdata = data.frame(FERTILIZER = seq(min(fert$FERTILIZER, na.rm = TRUE), max(fert$FERTILIZER, na.rm = TRUE), len = 1000)) fit = posterior_predict(fert.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("YIELD") + scale_x_continuous("FERTILIZER") + theme_classic()
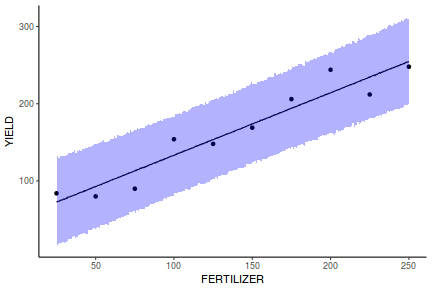 Show BRMS code
Show BRMS codelibrary(brms) resid = resid(fert.brm)[, "Estimate"] fit = fitted(fert.brm)[, "Estimate"] ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
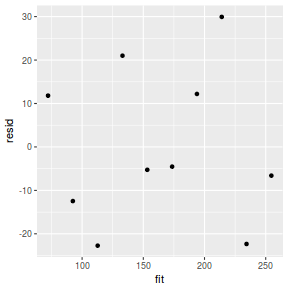
ggplot() + geom_point(data = NULL, aes(y = resid, x = fert$FERTILIZER))
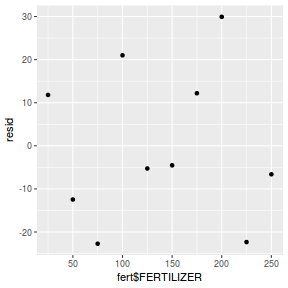
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
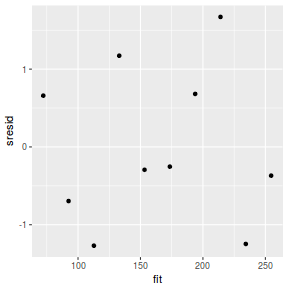
y_pred = posterior_predict(fert.brms)
Error in posterior_predict(fert.brms): object 'fert.brms' not found
newdata = fert %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -YIELD, -FERTILIZER) ggplot(newdata, aes(Value, x = FERTILIZER)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = fert, aes(y = YIELD, x = FERTILIZER), fill = "red", color = "red", alpha = 0.5)
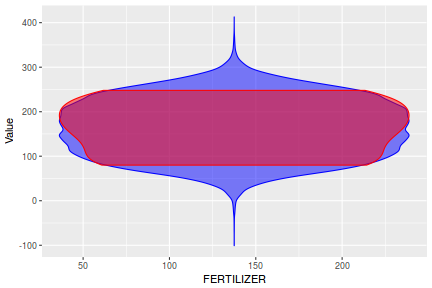
## Calculate the fitted values newdata = data.frame(FERTILIZER = seq(min(fert$FERTILIZER, na.rm = TRUE), max(fert$FERTILIZER, na.rm = TRUE), len = 1000)) fit = posterior_predict(fert.brm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("YIELD") + scale_x_continuous("FERTILIZER") + theme_classic()
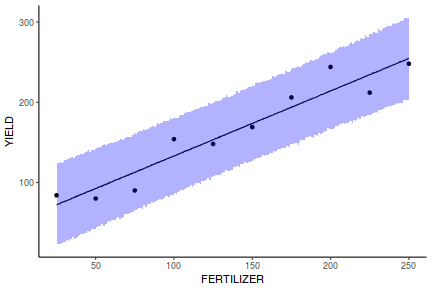
- Explore parameter estimates
Show MCMCpack code
library(MCMCpack) summary(fert.mcmcpack)
Iterations = 1001:11000 Thinning interval = 1 Number of chains = 1 Sample size per chain = 10000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE (Intercept) 52.1741 14.97636 0.1497636 0.1451274 FERTILIZER 0.8097 0.09708 0.0009708 0.0009146 sigma2 481.1315 323.12851 3.2312851 4.1585666 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% (Intercept) 22.6977 42.9486 52.1874 61.15 82.881 FERTILIZER 0.6143 0.7512 0.8102 0.87 1.002 sigma2 167.1821 281.7044 392.9891 568.26 1322.691library(broom) tidyMCMC(fert.mcmcpack, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 (Intercept) 52.1740843 14.97635880 21.3646092 81.114767 2 FERTILIZER 0.8097191 0.09707823 0.6181384 1.005315 3 sigma2 481.1315426 323.12850667 123.8952634 1089.733228
mcmcpvalue(fert.mcmcpack[, 2])
[1] 0
Show JAGS codelibrary(R2jags) print(fert.r2jags)
Inference for Bugs model at "../downloads/BUGSscripts/tut7.2bQ1_JAGS.txt", fit using jags, 3 chains, each with 166667 iterations (first 2000 discarded), n.thin = 10 n.sims = 49401 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff alpha 51.849 14.984 21.858 42.754 51.832 61.002 81.635 1.001 49000 beta 0.812 0.097 0.617 0.753 0.812 0.871 1.005 1.001 49000 sigma 21.026 6.133 12.857 16.795 19.811 23.835 36.260 1.001 49000 deviance 88.562 2.884 85.290 86.461 87.818 89.867 96.062 1.001 37000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 4.2 and DIC = 92.7 DIC is an estimate of expected predictive error (lower deviance is better).# OR library(broom) tidyMCMC(as.mcmc(fert.r2jags), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 alpha 51.8492738 14.98388244 21.8583517 81.642155 2 beta 0.8120709 0.09654881 0.6192913 1.006265 3 deviance 88.5621720 2.88386090 85.0412289 94.270274 4 sigma 21.0258884 6.13340577 11.4968165 32.881356
mcmcpvalue(fert.r2jags$BUGSoutput$sims.matrix[, c("beta")])
[1] 0
Show RSTAN codelibrary(rstan) summary(fert.rstan)
$summary mean se_mean sd 2.5% 25% 50% 75% beta[1] 0.809339 0.001224893 0.09133433 0.6302421 0.7536958 0.808977 0.8644469 cbeta0 162.911120 0.088746904 6.59606165 149.6686239 158.7781670 162.995295 167.1182082 sigma 19.755274 0.088886313 5.52011025 12.3522892 16.0198526 18.727561 22.2138427 beta0 51.627013 0.194446016 14.22664023 23.1531087 42.8389913 51.835282 60.1747185 lp__ -36.107824 0.024765438 1.46640854 -39.9064736 -36.7508815 -35.721599 -35.0529187 97.5% n_eff Rhat beta[1] 0.9943676 5559.958 1.000022 cbeta0 175.9175873 5524.119 1.000387 sigma 33.3456585 3856.788 1.000305 beta0 79.8334231 5353.115 1.000033 lp__ -34.4662193 3506.049 1.000220 $c_summary , , chains = chain:1 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8062179 0.09006342 0.6278512 0.7517994 0.8064476 0.8607343 0.9912481 cbeta0 162.8156913 6.55558914 149.5264160 158.6916828 162.8788927 167.1278693 175.8170642 sigma 19.7434368 5.54546922 12.3279034 15.9510823 18.8511934 22.2436079 33.3647357 beta0 51.9607351 14.14110561 23.4203535 43.1606609 52.0365182 60.6746148 80.9455324 lp__ -36.1251415 1.44746841 -39.8586983 -36.7754005 -35.7606787 -35.0631530 -34.4765177 , , chains = chain:2 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8101857 0.0908987 0.6351154 0.7529598 0.8102831 0.8655236 1.001964 cbeta0 162.8427059 6.6615603 149.5567338 158.6341487 163.0016877 167.0187024 175.783045 sigma 19.7644672 5.4723037 12.2371274 15.9932157 18.6477422 22.3340807 33.270306 beta0 51.4421703 14.2602676 23.1959990 42.5775876 51.5415815 60.1122890 79.674492 lp__ -36.1068651 1.4730745 -39.8942511 -36.7389338 -35.7200206 -35.0385177 -34.467814 , , chains = chain:3 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8116133 0.09297132 0.6290305 0.7566819 0.8104881 0.8672376 0.9899435 cbeta0 163.0749636 6.57038774 150.0552004 158.9972371 163.1267028 167.1366895 176.1365046 sigma 19.7579187 5.54467140 12.4973713 16.0894053 18.7061891 22.0596009 33.3351892 beta0 51.4781334 14.27858494 23.1574980 42.8290483 51.7703420 59.9094807 79.1162177 lp__ -36.0914654 1.47894973 -39.9818101 -36.7232619 -35.6896052 -35.0490553 -34.4629588# OR library(broom) tidyMCMC(fert.rstan, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 beta[1] 0.809339 0.09133433 0.6286141 0.9906276 2 cbeta0 162.911120 6.59606165 150.0733053 176.1017746 3 sigma 19.755274 5.52011025 10.8809881 30.0637007 4 beta0 51.627013 14.22664023 23.8893344 80.2856801
mcmcpvalue(as.matrix(fert.rstan)[, c("beta[2]")])
Error in as.matrix(fert.rstan)[, c("beta[2]")]: subscript out of boundsShow RSTANARM codelibrary(rstanarm) summary(fert.rstanarm)
Model Info: function: stan_glm family: gaussian [identity] formula: YIELD ~ FERTILIZER algorithm: sampling priors: see help('prior_summary') sample: 6750 (posterior sample size) num obs: 10 Estimates: mean sd 2.5% 25% 50% 75% 97.5% (Intercept) 52.3 16.4 20.0 42.4 52.2 61.9 85.5 FERTILIZER 0.8 0.1 0.6 0.7 0.8 0.9 1.0 sigma 22.7 7.5 13.4 17.8 21.1 25.8 41.6 mean_PPD 163.7 10.8 142.9 157.0 163.6 170.0 185.6 log-posterior -62.9 1.5 -66.8 -63.5 -62.5 -61.8 -61.2 Diagnostics: mcse Rhat n_eff (Intercept) 0.2 1.0 5424 FERTILIZER 0.0 1.0 6419 sigma 0.1 1.0 2775 mean_PPD 0.2 1.0 3774 log-posterior 0.0 1.0 2387 For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).# OR library(broom) tidyMCMC(fert.rstanarm$stanfit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 (Intercept) 52.3380468 16.3541986 19.1844357 84.055416 0.9998678 5424 2 FERTILIZER 0.8097014 0.1045031 0.5997843 1.012831 0.9997428 6419 3 sigma 22.7356331 7.4747818 12.1911517 36.856341 0.9999145 2775 4 mean_PPD 163.6570502 10.8247627 141.7715662 184.049507 1.0001552 3774 5 log-posterior -62.8815619 1.5021455 -65.8124268 -61.090052 0.9999853 2387
mcmcpvalue(as.matrix(fert.rstanarm)[, c("FERTILIZER")])
[1] 0
posterior_interval(fert.rstanarm, prob = 0.95)
2.5% 97.5% (Intercept) 19.9536145 85.512691 FERTILIZER 0.6049777 1.018857 sigma 13.4087337 41.584921
(full = loo(fert.rstanarm))
Computed from 6750 by 10 log-likelihood matrix Estimate SE elpd_loo -45.9 1.4 p_loo 2.2 0.5 looic 91.8 2.8 Pareto k diagnostic values: Count Pct (-Inf, 0.5] (good) 9 90.0% (0.5, 0.7] (ok) 1 10.0% (0.7, 1] (bad) 0 0.0% (1, Inf) (very bad) 0 0.0% All Pareto k estimates are ok (k < 0.7) See help('pareto-k-diagnostic') for details.(reduced = loo(update(fert.rstanarm, formula = . ~ 1)))
Gradient evaluation took 2.3e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.23 seconds. Adjust your expectations accordingly! Elapsed Time: 0.039963 seconds (Warm-up) 0.077622 seconds (Sampling) 0.117585 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 0.03145 seconds (Warm-up) 0.088448 seconds (Sampling) 0.119898 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 0.030714 seconds (Warm-up) 0.088801 seconds (Sampling) 0.119515 seconds (Total)Computed from 6750 by 10 log-likelihood matrix Estimate SE elpd_loo -57.2 1.1 p_loo 1.2 0.2 looic 114.4 2.3 All Pareto k estimates are good (k < 0.5) See help('pareto-k-diagnostic') for details.par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
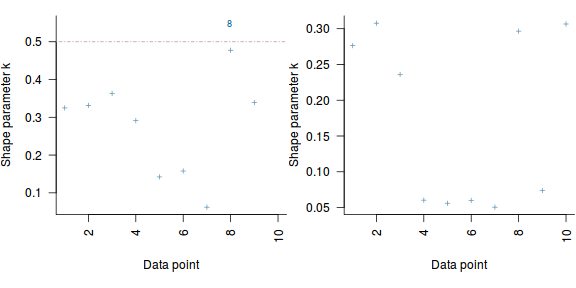
compare_models(full, reduced)
elpd_diff se -11.3 1.5Show BRMS codelibrary(brms) summary(fert.brm)
Family: gaussian(identity) Formula: YIELD ~ FERTILIZER Data: fert (Number of observations: 10) Samples: 3 chains, each with iter = 5000; warmup = 500; thin = 2; total post-warmup samples = 6750 ICs: LOO = Not computed; WAIC = Not computed Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept 51.92 14.72 22.46 81.83 6260 1 FERTILIZER 0.81 0.10 0.61 1.00 6326 1 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma 21.03 5.77 13 35.05 5190 1 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1).# OR library(broom) tidyMCMC(fert.brm$fit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 b_Intercept 51.9228855 14.71902757 22.1522286 81.4263823 0.9998708 6260 2 b_FERTILIZER 0.8107323 0.09515934 0.6106665 0.9943814 0.9998047 6326 3 sigma 21.0256275 5.77415796 11.9385908 32.5465719 1.0000062 5190
mcmcpvalue(as.matrix(fert.brm)[, c("b_FERTILIZER")])
[1] 0
posterior_interval(as.matrix(fert.brm), prob = 0.95)
2.5% 97.5% b_Intercept 22.462644 81.8312739 b_FERTILIZER 0.613901 0.9995781 sigma 12.995195 35.0498366 lp__ -36.063369 -31.0011369
(full = loo(fert.brm))
LOOIC SE 91.21 3.18
(reduced = loo(update(fert.brm, formula = . ~ 1)))
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Gradient evaluation took 7e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.031218 seconds (Warm-up) 0.022592 seconds (Sampling) 0.05381 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Gradient evaluation took 4e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.031854 seconds (Warm-up) 0.022912 seconds (Sampling) 0.054766 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Gradient evaluation took 3e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.030551 seconds (Warm-up) 0.023864 seconds (Sampling) 0.054415 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.031004 seconds (Warm-up) 0.022572 seconds (Sampling) 0.053576 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Gradient evaluation took 3e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.031758 seconds (Warm-up) 0.022977 seconds (Sampling) 0.054735 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Gradient evaluation took 4e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.030404 seconds (Warm-up) 0.024019 seconds (Sampling) 0.054423 seconds (Total)LOOIC SE 114.12 2.85
par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
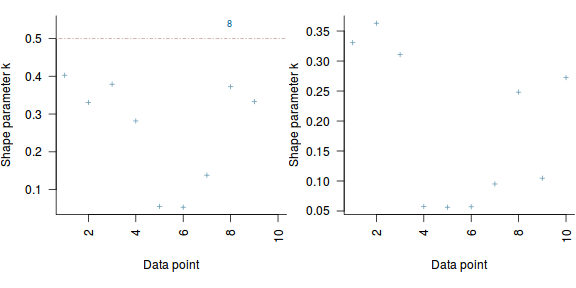
- Generate graphical summaries
Show MCMCpack code
library(MCMCpack) fert.mcmc = fert.mcmcpack ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^{ -1 }))) + theme_classic()
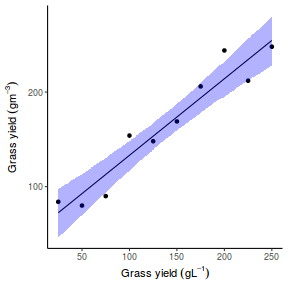
library(MCMCpack) fert.mcmc = fert.mcmcpack ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit)) newdata = newdata %>% gather(key = Sample, value = fit, -FERTILIZER, -YIELD) newdata.sum = newdata %>% group_by(FERTILIZER) %>% dplyr:::summarize(fit = median(fit)) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_line(aes(y = fit, x = FERTILIZER, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = FERTILIZER), color = "blue") + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER), color = "red") + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^-1))) + theme_classic()
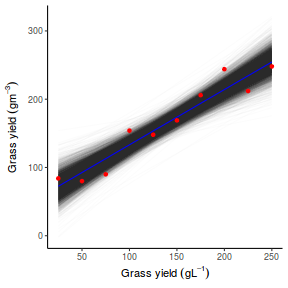 Show JAGS code
Show JAGS codelibrary(MCMCpack) fert.mcmc = fert.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^{ -1 }))) + theme_classic()
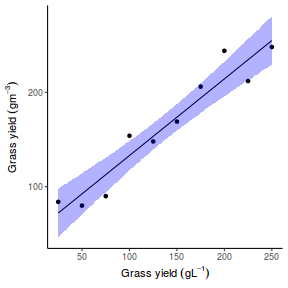
library(MCMCpack) fert.mcmc = fert.mcmcpack ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("beta0", "beta1")]
Error in `[.default`(fert.mcmc, , c("beta0", "beta1")): subscript out of boundsfit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit)) newdata = newdata %>% gather(key = Sample, value = fit, -FERTILIZER, -YIELD) newdata.sum = newdata %>% group_by(FERTILIZER) %>% dplyr:::summarize(fit = median(fit)) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_line(aes(y = fit, x = FERTILIZER, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = FERTILIZER), color = "blue") + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER), color = "red") + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^-1))) + theme_classic()
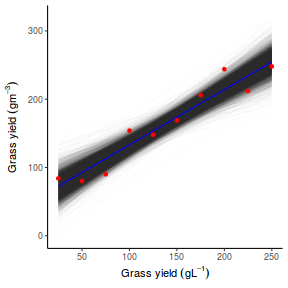 Show RSTAN code
Show RSTAN codelibrary(MCMCpack) fert.mcmc = as.matrix(fert.rstan) ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^{ -1 }))) + theme_classic()
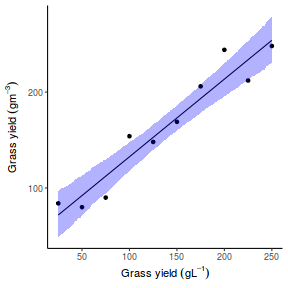
library(MCMCpack) fert.mcmc = as.matrix(fert.rstan) ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit)) newdata = newdata %>% gather(key = Sample, value = fit, -FERTILIZER, -YIELD) newdata.sum = newdata %>% group_by(FERTILIZER) %>% dplyr:::summarize(fit = median(fit)) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_line(aes(y = fit, x = FERTILIZER, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = FERTILIZER), color = "blue") + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER), color = "red") + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^-1))) + theme_classic()
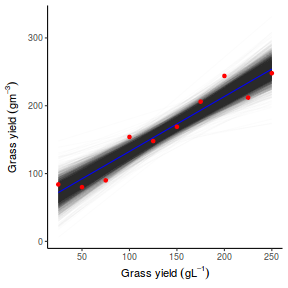 Show RSTANARM code
Show RSTANARM codenewdata = newdata = new_data(fert, seq = "FERTILIZER", length = 1000) fit = posterior_linpred(fert.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^{ -1 }))) + theme_classic()
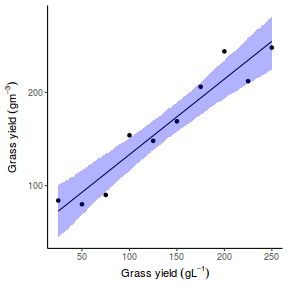
library(rstanarm) fert.mcmc = as.matrix(fert.rstanarm) ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("(Intercept)", "FERTILIZER")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit)) newdata = newdata %>% gather(key = Sample, value = fit, -FERTILIZER, -YIELD) newdata.sum = newdata %>% group_by(FERTILIZER) %>% dplyr:::summarize(fit = median(fit)) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_line(aes(y = fit, x = FERTILIZER, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = FERTILIZER), color = "blue") + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER), color = "red") + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^-1))) + theme_classic()
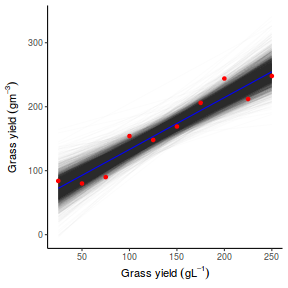 Show BRMS code
Show BRMS codenewdata = marginal_effects(fert.brm)$FERTILIZER ggplot(newdata, aes(y = estimate__, x = FERTILIZER)) + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER)) + geom_line() + geom_ribbon(aes(ymin = lower__, ymax = upper__), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^{ -1 }))) + theme_classic()
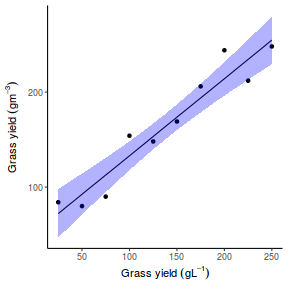
library(brms) fert.mcmc = as.matrix(fert.brm) ## Calculate the fitted values library(newdata) newdata = new_data(fert, seq = "FERTILIZER", length = 1000) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("b_Intercept", "b_FERTILIZER")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit)) newdata = newdata %>% gather(key = Sample, value = fit, -FERTILIZER, -YIELD) newdata.sum = newdata %>% group_by(FERTILIZER) %>% dplyr:::summarize(fit = median(fit)) ggplot(newdata, aes(y = estimate, x = FERTILIZER)) + geom_line(aes(y = fit, x = FERTILIZER, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = FERTILIZER), color = "blue") + geom_point(data = fert, aes(y = YIELD, x = FERTILIZER), color = "red") + scale_y_continuous(expression(Grass ~ yield ~ (g * m^-3))) + scale_x_continuous(expression(Grass ~ yield ~ (g * L^-1))) + theme_classic()
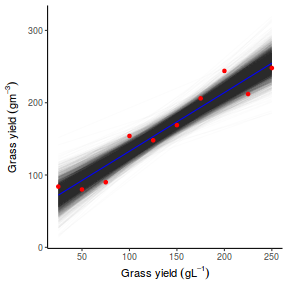
- Explore effect sizes
Show MCMCpack code
library(MCMCpack) fert.mcmc = fert.mcmcpack newdata = with(fert, data.frame(FERTILIZER = c(min(FERTILIZER, na.rm = TRUE), max(FERTILIZER, na.rm = TRUE)))) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("(Intercept)", "FERTILIZER")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 182.1868 21.8426 139.0811 226.1958
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/sqrt(fert.mcmc[, "sigma2"]) (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 9.288865 2.569286 4.40718 14.36279
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 262.2656 298.5128 122.3063 426.8095
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 2e-04
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 3.622656 2.985128 2.223063 5.268095
Show JAGS codelibrary(R2jags) fert.mcmc = fert.r2jags$BUGSoutput$sims.matrix newdata = with(fert, data.frame(FERTILIZER = c(min(FERTILIZER, na.rm = TRUE), max(FERTILIZER, na.rm = TRUE)))) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 182.716 21.72348 139.3406 226.4097
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/fert.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 9.326646 2.559971 4.446114 14.37503
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 267.7493 140.0571 126.1084 433.3658
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.0001416975
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 3.677493 1.400571 2.261084 5.333658
Show RSTAN codelibrary(rstan) fert.mcmc = as.matrix(fert.rstan) newdata = with(fert, data.frame(FERTILIZER = c(min(FERTILIZER, na.rm = TRUE), max(FERTILIZER, na.rm = TRUE)))) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 182.1013 20.55022 141.4382 222.8912
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/fert.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 9.829208 2.571008 4.981677 15.01005
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 267.2579 99.26202 139.4832 431.2538
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 3.672579 0.9926202 2.394832 5.312538
Show RSTANARM codelibrary(rstanarm) fert.mcmc = as.matrix(fert.rstanarm) newdata = with(fert, data.frame(FERTILIZER = c(min(FERTILIZER, na.rm = TRUE), max(FERTILIZER, na.rm = TRUE)))) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("(Intercept)", "FERTILIZER")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 182.1828 23.51321 134.9515 227.8871
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/fert.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 8.71441 2.569302 3.801572 13.73853
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 252.7138 923.965 104.8493 434.5145
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.0005925926
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 3.527138 9.23965 2.048493 5.345145
Show BRMS codelibrary(brms) fert.mcmc = as.matrix(fert.brm) newdata = with(fert, data.frame(FERTILIZER = c(min(FERTILIZER, na.rm = TRUE), max(FERTILIZER, na.rm = TRUE)))) Xmat = model.matrix(~FERTILIZER, newdata) coefs = fert.mcmc[, c("b_Intercept", "b_FERTILIZER")] fit = coefs %*% t(Xmat) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 182.4148 21.41085 137.4 223.7358
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/fert.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 9.266529 2.498071 4.514346 14.21276
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 266.801 91.17899 128.9894 434.6131
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 3.66801 0.9117899 2.289894 5.346131
- Explore finite-population standard deviations
Show MCMCpack code
library(MCMCpack) library(broom) fert.mcmc = fert.mcmcpack sd.FERTILIZER = abs(fert.mcmc[, "FERTILIZER"]) * sd(fert$FERTILIZER) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = fert.mcmc[, 1:2] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$YIELD, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.FERTILIZER, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 61.28866 7.347973 46.78768 76.09352 2 sd.resid 19.24431 2.127803 17.91277 23.15467
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 77.19688 3.476627 69.65459 78.12506 2 sd.resid 22.80312 3.476627 21.87494 30.34541
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
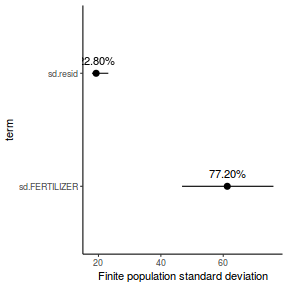 Show JAGS code
Show JAGS codelibrary(R2jags) library(broom) fert.mcmc = fert.r2jags$BUGSoutput$sims.matrix sd.FERTILIZER = abs(fert.mcmc[, "beta"]) * sd(fert$FERTILIZER) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = fert.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$YIELD, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.FERTILIZER, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 61.46667 7.307901 46.87494 76.16548 2 sd.resid 19.23513 2.069818 17.91277 23.14717
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 77.21399 3.237124 69.88457 78.12506 2 sd.resid 22.78601 3.237124 21.87494 30.11543
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
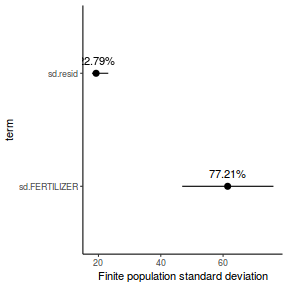 Show RSTAN code
Show RSTAN codelibrary(rstan) library(broom) fert.mcmc = as.matrix(fert.rstan) sd.FERTILIZER = abs(fert.mcmc[, "beta[1]"]) * sd(fert$FERTILIZER) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = fert.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$YIELD, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.FERTILIZER, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 61.25988 6.913210 47.58059 74.98185 2 sd.resid 19.10316 1.935704 17.91277 22.61032
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 77.20433 3.192041 70.37898 78.12506 2 sd.resid 22.79567 3.192041 21.87494 29.62102
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
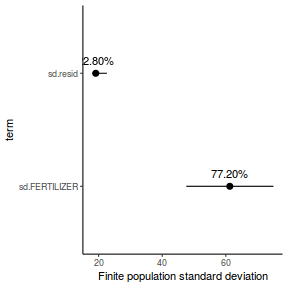 Show RSTANARM code
Show RSTANARM codelibrary(rstanarm) library(broom) fert.mcmc = as.matrix(fert.rstanarm) sd.FERTILIZER = abs(fert.mcmc[, "FERTILIZER"]) * sd(fert$FERTILIZER) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = fert.mcmc[, c("(Intercept)", "FERTILIZER")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$YIELD, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.FERTILIZER, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 61.28732 7.909974 45.39843 76.66249 2 sd.resid 19.42438 2.477229 17.91277 23.81033
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 77.11062 3.719985 68.86628 78.12506 2 sd.resid 22.88938 3.719985 21.87494 31.13372
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
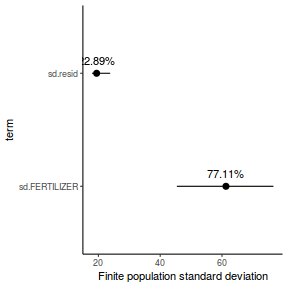 Show BRMS code
Show BRMS codelibrary(brms) library(broom) fert.mcmc = as.matrix(fert.brm) sd.FERTILIZER = abs(fert.mcmc[, "b_FERTILIZER"]) * sd(fert$FERTILIZER) # generate a model matrix newdata = data.frame(FERTILIZER = fert$FERTILIZER) Xmat = model.matrix(~FERTILIZER, newdata) ## get median parameter estimates coefs = fert.mcmc[, c("b_Intercept", "b_FERTILIZER")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$YIELD, "-") sd.resid = apply(resid, 1, sd) sd.all = cbind(sd.FERTILIZER, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 61.36535 7.202730 46.22211 75.26598 2 sd.resid 19.20309 1.995814 17.91277 23.12029
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.FERTILIZER 77.22118 3.232889 69.63626 78.12506 2 sd.resid 22.77882 3.232889 21.87494 30.36374
## we can even plot this as a Bayesian ANOVA table ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
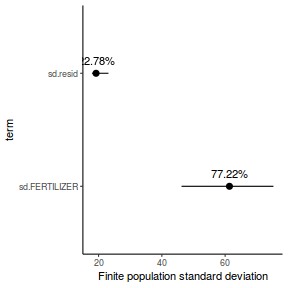
- Explore $R^2$
Show MCMCpack code
library(MCMCpack) library(broom) fert.mcmc <- fert.mcmcpack Xmat = model.matrix(~FERTILIZER, data = fert) coefs = fert.mcmc[, c("(Intercept)", "FERTILIZER")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$FERTILIZER, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.9257774 0.08018707 0.7802406 1
# for comparison with frequentist summary(lm(YIELD ~ FERTILIZER, data = fert))
Call: lm(formula = YIELD ~ FERTILIZER, data = fert) Residuals: Min 1Q Median 3Q Max -22.79 -11.07 -5.00 12.00 29.79 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 51.93333 12.97904 4.001 0.00394 ** FERTILIZER 0.81139 0.08367 9.697 1.07e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 19 on 8 degrees of freedom Multiple R-squared: 0.9216, Adjusted R-squared: 0.9118 F-statistic: 94.04 on 1 and 8 DF, p-value: 1.067e-05Show JAGS codelibrary(R2jags) library(broom) fert.mcmc <- fert.r2jags$BUGSoutput$sims.matrix Xmat = model.matrix(~FERTILIZER, data = fert) coefs = fert.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$FERTILIZER, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.9276763 0.07600148 0.7851166 1
# for comparison with frequentist summary(lm(YIELD ~ FERTILIZER, data = fert))
Call: lm(formula = YIELD ~ FERTILIZER, data = fert) Residuals: Min 1Q Median 3Q Max -22.79 -11.07 -5.00 12.00 29.79 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 51.93333 12.97904 4.001 0.00394 ** FERTILIZER 0.81139 0.08367 9.697 1.07e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 19 on 8 degrees of freedom Multiple R-squared: 0.9216, Adjusted R-squared: 0.9118 F-statistic: 94.04 on 1 and 8 DF, p-value: 1.067e-05Show RSTAN codelibrary(rstan) library(broom) fert.mcmc <- as.matrix(fert.rstan) Xmat = model.matrix(~FERTILIZER, data = fert) coefs = fert.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$FERTILIZER, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.9280336 0.07363253 0.795127 1
# for comparison with frequentist summary(lm(YIELD ~ FERTILIZER, data = fert))
Call: lm(formula = YIELD ~ FERTILIZER, data = fert) Residuals: Min 1Q Median 3Q Max -22.79 -11.07 -5.00 12.00 29.79 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 51.93333 12.97904 4.001 0.00394 ** FERTILIZER 0.81139 0.08367 9.697 1.07e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 19 on 8 degrees of freedom Multiple R-squared: 0.9216, Adjusted R-squared: 0.9118 F-statistic: 94.04 on 1 and 8 DF, p-value: 1.067e-05Show RSTANARM codelibrary(rstanarm) library(broom) fert.mcmc <- as.matrix(fert.rstanarm) Xmat = model.matrix(~FERTILIZER, data = fert) coefs = fert.mcmc[, c("(Intercept)", "FERTILIZER")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$FERTILIZER, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.9229182 0.08473831 0.7641056 1
# for comparison with frequentist summary(lm(YIELD ~ FERTILIZER, data = fert))
Call: lm(formula = YIELD ~ FERTILIZER, data = fert) Residuals: Min 1Q Median 3Q Max -22.79 -11.07 -5.00 12.00 29.79 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 51.93333 12.97904 4.001 0.00394 ** FERTILIZER 0.81139 0.08367 9.697 1.07e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 19 on 8 degrees of freedom Multiple R-squared: 0.9216, Adjusted R-squared: 0.9118 F-statistic: 94.04 on 1 and 8 DF, p-value: 1.067e-05Show BRMS codelibrary(brms) library(broom) fert.mcmc <- as.matrix(fert.brm) Xmat = model.matrix(~FERTILIZER, data = fert) coefs = fert.mcmc[, c("b_Intercept", "b_FERTILIZER")] fit = coefs %*% t(Xmat) resid = sweep(fit, 2, fert$FERTILIZER, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.9271947 0.07609225 0.7798637 1
# for comparison with frequentist summary(lm(YIELD ~ FERTILIZER, data = fert))
Call: lm(formula = YIELD ~ FERTILIZER, data = fert) Residuals: Min 1Q Median 3Q Max -22.79 -11.07 -5.00 12.00 29.79 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 51.93333 12.97904 4.001 0.00394 ** FERTILIZER 0.81139 0.08367 9.697 1.07e-05 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 19 on 8 degrees of freedom Multiple R-squared: 0.9216, Adjusted R-squared: 0.9118 F-statistic: 94.04 on 1 and 8 DF, p-value: 1.067e-05
Simple linear regression
Christensen et al. (1996) studied the relationships between coarse woody debris (CWD) and, shoreline vegetation and lake development in a sample of 16 lakes. They defined CWD as debris greater than 5cm in diameter and recorded, for a number of plots on each lake, the basal area (m2.km-1) of CWD in the nearshore water, and the density (no.km-1) of riparian trees along the shore. The data are in the file christ.csv and the relevant variables are the response variable, CWDBASAL (coarse woody debris basal area, m2.km-1), and the predictor variable, RIPDENS (riparian tree density, trees.km-1).
Download Christensen data set| Format of christ.csv data files | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
|||||||||||||||||||||||||||
christ <- read.table("../downloads/data/christ.csv", header = T, sep = ",", strip.white = T) head(christ)
LAKE RIPDENS CWDBASAL 1 Bay 1270 121 2 Bergner 1210 41 3 Crampton 1800 183 4 Long 1875 130 5 Roach 1300 127 6 Tenderfoot 2150 134
-
The researchers were most likely interested in investigating whether there was a relationship between course woody debris basal area and the density of riparian vegetation.
Write out an appropriate linear model.
-
Perform exploratory data analysis to help guide what sort of analysis will be suitable
and whether the various assumptions are likely to be met.
Show code
ggplot(christ, aes(y = CWDBASAL, x = RIPDENS)) + geom_point() + geom_smooth()
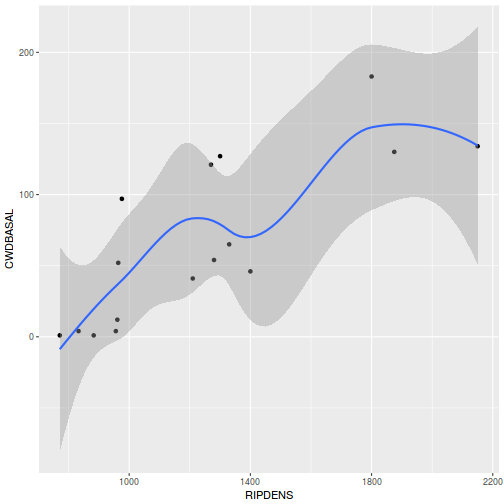
ggplot(christ, aes(y = CWDBASAL, x = 1)) + geom_boxplot()
ggplot(christ, aes(y = RIPDENS, x = 1)) + geom_boxplot()
-
Fit the appropriate Bayesian model.
Show MCMCpack code
library(MCMCpack) christ.mcmcpack = MCMCregress(CWDBASAL ~ RIPDENS, data = christ)
Show JAGS codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha+beta*x[i] } #Priors alpha ~ dnorm (0.01,1.0E-6) beta ~ dnorm(0,1.0E-6) tau <- 1 / (sigma * sigma) sigma~dgamma(0.001,0.001) } " christ.list <- with(christ, list(x=RIPDENS, y=CWDBASAL,n=nrow(christ)) ) params <- c("alpha","beta","sigma") burnInSteps = 2000 nChains = 3 numSavedSteps = 50000 thinSteps = 10 nIter = ceiling((numSavedSteps * thinSteps)/nChains) christ.r2jags <- jags(data=christ.list, inits=NULL, #or inits=list(inits,inits,inits) # since there are three chains parameters.to.save=params, model.file=textConnection(modelString), #"../downloads/BUGSscripts/tut7.2bQ1_JAGS.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph information: Observed stochastic nodes: 16 Unobserved stochastic nodes: 3 Total graph size: 77 Initializing model
Show RSTAN codemodelString = " data { int<lower=1> n; // total number of observations vector[n] Y; // response variable int<lower=1> nX; // number of effects matrix[n, nX] X; // model matrix } ransformed data { matrix[n, nX - 1] Xc; // centered version of X vector[nX - 1] means_X; // column means of X before centering for (i in 2:nX) { means_X[i - 1] = mean(X[, i]); Xc[, i - 1] = X[, i] - means_X[i - 1]; } } parameters { vector[nX-1] beta; // population-level effects real cbeta0; // center-scale intercept real<lower=0> sigma; // residual SD } ransformed parameters { } model { vector[n] mu; mu = Xc * beta + cbeta0; // prior specifications beta ~ normal(0, 100); cbeta0 ~ normal(0, 100); sigma ~ cauchy(0, 5); // likelihood contribution Y ~ normal(mu, sigma); } generated quantities { real beta0; // population-level intercept beta0 = cbeta0 - dot_product(means_X, beta); } " Xmat <- model.matrix(~RIPDENS, data = christ) christ.list <- with(christ, list(Y = CWDBASAL, X = Xmat, nX = ncol(Xmat), n = nrow(christ))) library(rstan) christ.rstan <- stan(data = christ.list, model_code = modelString, chains = 3, iter = 5000, warmup = 500, thin = 2)
SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 1). Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.031024 seconds (Warm-up) 0.075979 seconds (Sampling) 0.107003 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 2). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.019954 seconds (Warm-up) 0.06602 seconds (Sampling) 0.085974 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 3). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.050727 seconds (Warm-up) 0.076632 seconds (Sampling) 0.127359 seconds (Total)Show RSTANARM codechrist.rstanarm = stan_glm(CWDBASAL ~ RIPDENS, data = christ, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior_intercept = normal(0, 1000), prior = normal(0, 1000), prior_aux = cauchy(0, 25))
Gradient evaluation took 3.7e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.37 seconds. Adjust your expectations accordingly! Elapsed Time: 2.76309 seconds (Warm-up) 1.68553 seconds (Sampling) 4.44862 seconds (Total) Gradient evaluation took 1.1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds. Adjust your expectations accordingly! Elapsed Time: 1.85513 seconds (Warm-up) 1.09875 seconds (Sampling) 2.95388 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 3.49276 seconds (Warm-up) 1.17575 seconds (Sampling) 4.66851 seconds (Total)Show BRMS codechrist.brm = brm(CWDBASAL ~ RIPDENS, data = christ, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior = c(prior(normal(0, 1000), class = "Intercept"), prior(normal(0, 1000), class = "b"), prior(cauchy(0, 25), class = "sigma")))
Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 0.041827 seconds (Warm-up) 0.067657 seconds (Sampling) 0.109484 seconds (Total) Gradient evaluation took 1.2e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds. Adjust your expectations accordingly! Elapsed Time: 0.037164 seconds (Warm-up) 0.0659 seconds (Sampling) 0.103064 seconds (Total) Gradient evaluation took 6e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds. Adjust your expectations accordingly! Elapsed Time: 0.030273 seconds (Warm-up) 0.085104 seconds (Sampling) 0.115377 seconds (Total) - Explore MCMC diagnostics
Show MCMCpack code
library(MCMCpack) plot(christ.mcmcpack)
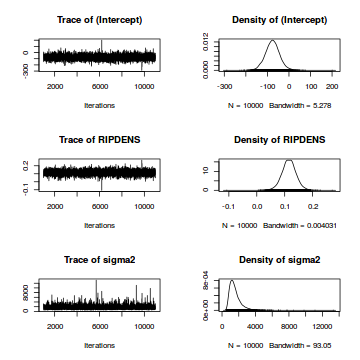
raftery.diag(christ.mcmcpack)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) (Intercept) 3 4028 3746 1.080 RIPDENS 2 3914 3746 1.040 sigma2 2 3680 3746 0.982autocorr.diag(christ.mcmcpack)
(Intercept) RIPDENS sigma2 Lag 0 1.000000000 1.000000000 1.000000000 Lag 1 0.011287106 0.004374026 0.162987189 Lag 5 -0.004110531 0.001777689 0.008242103 Lag 10 -0.015174763 -0.014133085 0.002405411 Lag 50 -0.003762082 -0.006531493 -0.009647390
Show JAGS codelibrary(R2jags) library(coda) christ.mcmc = as.mcmc(christ.r2jags) plot(christ.mcmc)
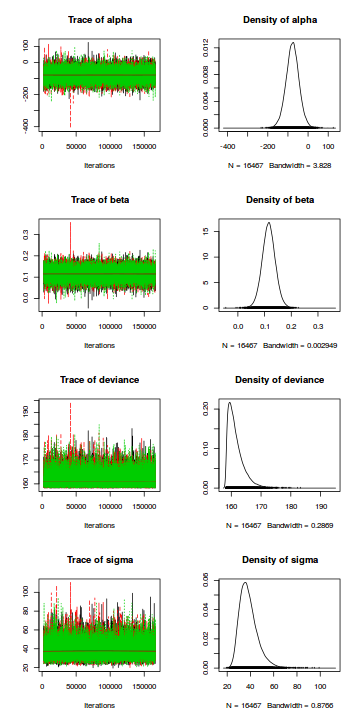
raftery.diag(christ.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 37830 3746 10.10 beta 20 37270 3746 9.95 deviance 20 37640 3746 10.00 sigma 10 37440 3746 9.99 [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 37830 3746 10.10 beta 20 37830 3746 10.10 deviance 10 37440 3746 9.99 sigma 20 38020 3746 10.10 [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 37640 3746 10.00 beta 20 37640 3746 10.00 deviance 20 36710 3746 9.80 sigma 20 37000 3746 9.88autocorr.diag(christ.mcmc)
alpha beta deviance sigma Lag 0 1.0000000000 1.0000000000 1.000000000 1.000000e+00 Lag 10 -0.0009480939 -0.0001283899 0.002458865 3.570752e-03 Lag 50 0.0091996629 0.0044812666 -0.003176260 -3.782869e-03 Lag 100 0.0001015533 -0.0003768049 0.001761242 -7.936498e-05 Lag 500 0.0061069559 0.0054183924 0.004162177 5.187498e-04
Show RSTAN codelibrary(rstan) library(coda) s = as.array(christ.rstan) christ.mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(christ.mcmc)
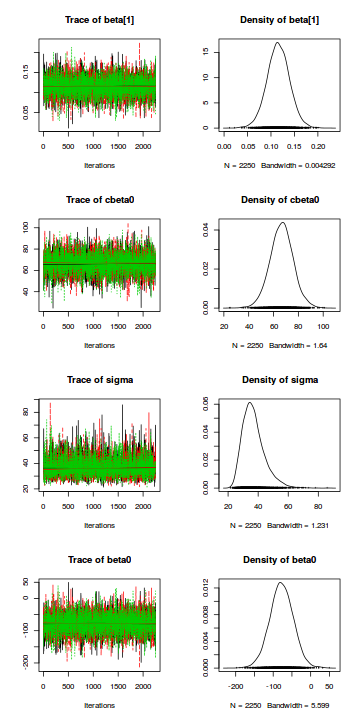
raftery.diag(christ.mcmc)
$`1` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`2` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`3` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(christ.mcmc)
beta[1] cbeta0 sigma beta0 Lag 0 1.000000000 1.000000000 1.0000000000 1.0000000000 Lag 1 0.047995261 0.034159169 0.0738886641 0.0508115262 Lag 5 -0.010886901 -0.027535766 0.0049054884 -0.0127033106 Lag 10 -0.016754669 0.011014910 0.0004265406 -0.0101132742 Lag 50 0.001727158 -0.006262706 -0.0052488064 -0.0008333885
library(rstan) library(coda) stan_ac(christ.rstan)
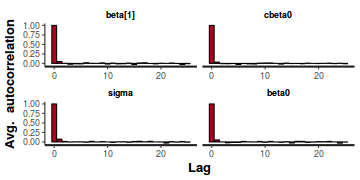
stan_rhat(christ.rstan)
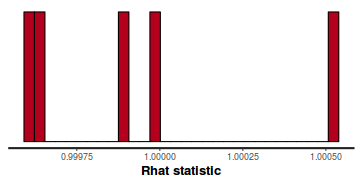
stan_ess(christ.rstan)
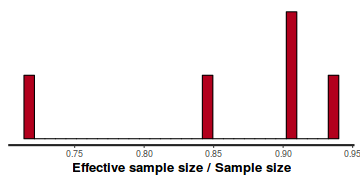
# using Bayeseplot library(bayesplot) detach("package:reshape") mcmc_trace(as.array(christ.rstan))
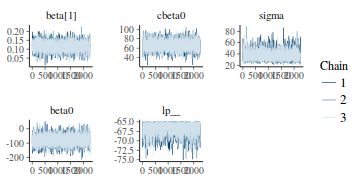
mcmc_trace(as.array(christ.rstan), regex_pars = "beta|sigma")
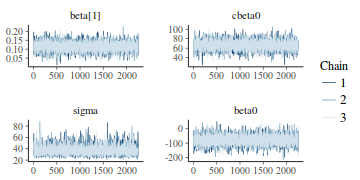
mcmc_dens(as.array(christ.rstan))
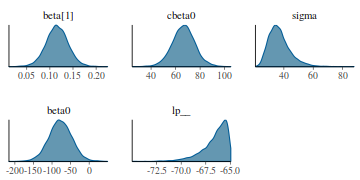
detach("package:reshape") library(bayesplot) mcmc_combo(as.array(christ.rstan))
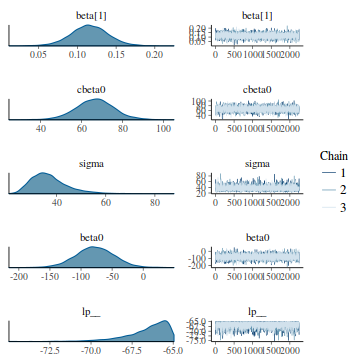 Show RSTANARM code
Show RSTANARM codelibrary(rstan) library(coda) s = as.array(christ.rstanarm) christ.mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(christ.mcmc)
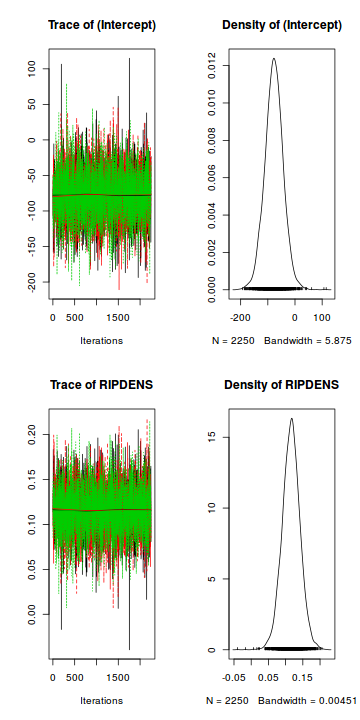
raftery.diag(christ.mcmc)
$`1` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`2` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`3` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(christ.mcmc)
(Intercept) RIPDENS Lag 0 1.000000000 1.000000000 Lag 1 0.041291203 0.010643546 Lag 5 -0.005398754 -0.009086948 Lag 10 0.002417242 -0.003359512 Lag 50 -0.010695723 -0.010799876
library(rstan) library(coda) stan_ac(christ.rstanarm)
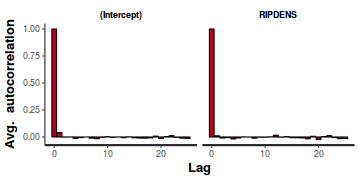
stan_rhat(christ.rstanarm)
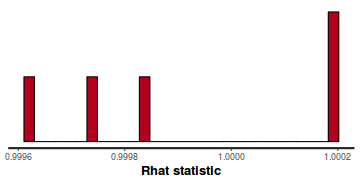
stan_ess(christ.rstanarm)
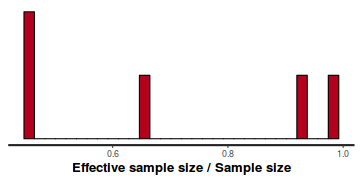
# using Bayeseplot library(bayesplot) detach("package:reshape") mcmc_trace(as.array(christ.rstanarm))
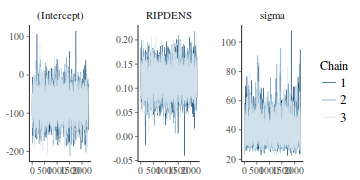
mcmc_trace(as.array(christ.rstanarm), regex_pars = "Intercept|x|sigma")
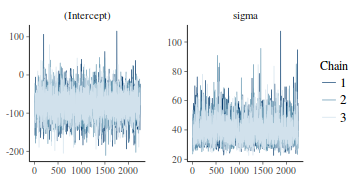
mcmc_dens(as.array(christ.rstan))
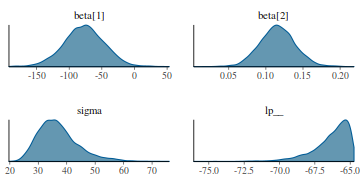
detach("package:reshape") library(bayesplot) mcmc_combo(as.array(christ.rstanarm))
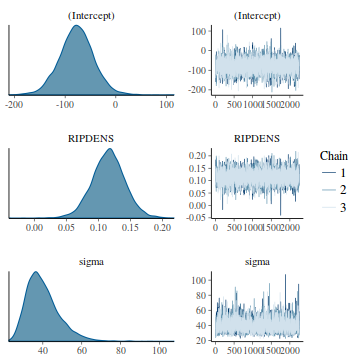
library(rstanarm) posterior_vs_prior(christ.rstanarm, color_by = "vs", group_by = TRUE, facet_args = list(scales = "free_y"))
Gradient evaluation took 2.1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.21 seconds. Adjust your expectations accordingly! Elapsed Time: 3.62107 seconds (Warm-up) 0.036939 seconds (Sampling) 3.65801 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 3.67508 seconds (Warm-up) 0.057926 seconds (Sampling) 3.73301 seconds (Total)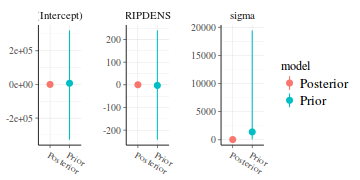 Show BRMS code
Show BRMS codelibrary(coda) library(brms) christ.mcmc = as.mcmc(christ.brm) plot(christ.mcmc)
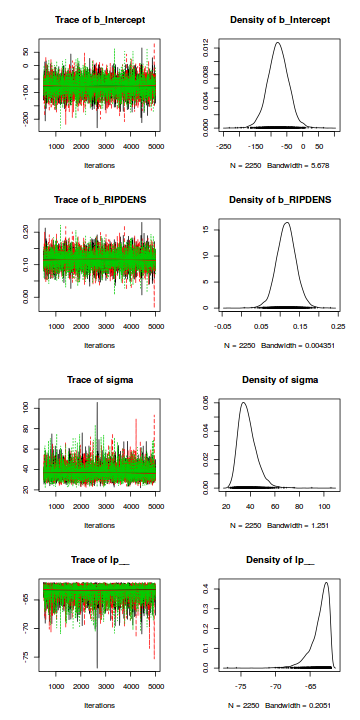
raftery.diag(christ.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(christ.mcmc)
Error in ts(x, start = start(x), end = end(x), deltat = thin(x)): invalid time series parameters specified
library(coda) stan_ac(christ.brm$fit)
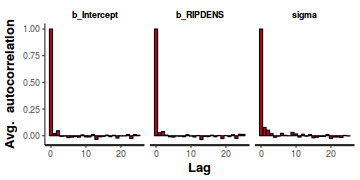
stan_rhat(christ.brm$fit)
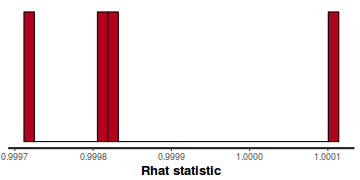
stan_ess(christ.brm$fit)
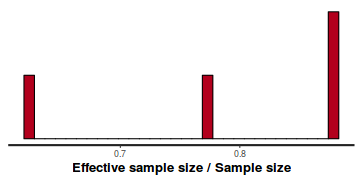
- Perform model validation
Show MCMCpack code
library(MCMCpack) christ.mcmc = as.data.frame(christ.mcmcpack) # generate a model matrix newdata = data.frame(RIPDENS = christ$RIPDENS) Xmat = model.matrix(~RIPDENS, newdata) ## get median parameter estimates coefs = apply(christ.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = christ$CWDBASAL - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
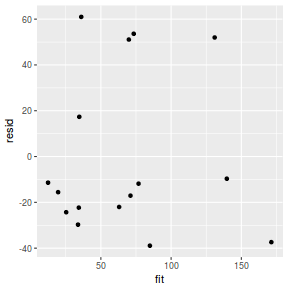
library(MCMCpack) christ.mcmc = as.data.frame(christ.mcmcpack) # generate a model matrix newdata = data.frame(RIPDENS = christ$RIPDENS) Xmat = model.matrix(~RIPDENS, newdata) ## get median parameter estimates coefs = apply(christ.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = christ$CWDBASAL - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = christ$RIPDENS))
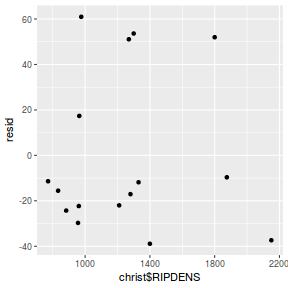
library(MCMCpack) christ.mcmc = as.data.frame(christ.mcmcpack) # generate a model matrix newdata = data.frame(RIPDENS = christ$RIPDENS) Xmat = model.matrix(~RIPDENS, newdata) ## get median parameter estimates coefs = apply(christ.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = christ$CWDBASAL - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
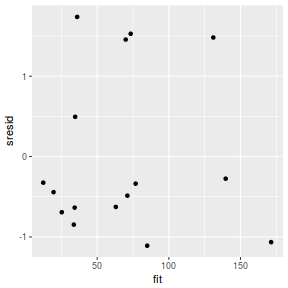
library(MCMCpack) christ.mcmc = as.matrix(christ.mcmcpack) # generate a model matrix Xmat = model.matrix(~RIPDENS, christ) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(christ.mcmc), function(i) rnorm(nrow(christ), fit[i, ], sqrt(christ.mcmc[i, "sigma2"]))) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = christ, aes(x = CWDBASAL, fill = "Obs"), alpha = 0.5)
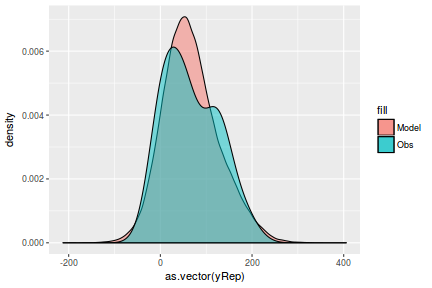
## Plot predicted effects library(MCMCpack) christ.mcmc = as.matrix(christ.mcmcpack) # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) fit = apply(fit, 2, function(x) rnorm(length(x), x, sqrt(christ.mcmc[, "sigma2"]))) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
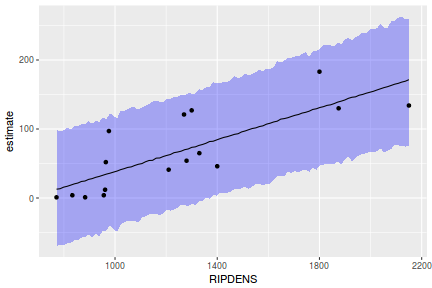
## Plot effects library(MCMCpack) christ.mcmc = as.matrix(christ.mcmcpack) # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
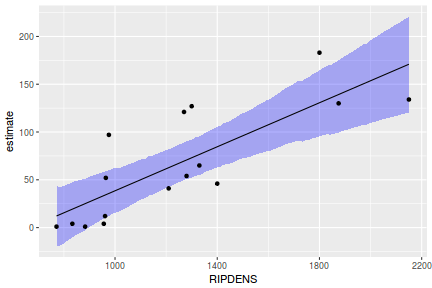 Show JAGS code
Show JAGS codelibrary(R2jags) christ.mcmc = christ.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = data.frame(RIPDENS = christ$RIPDENS) Xmat = model.matrix(~RIPDENS, newdata) ## get median parameter estimates coefs = apply(christ.mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = christ$CWDBASAL - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
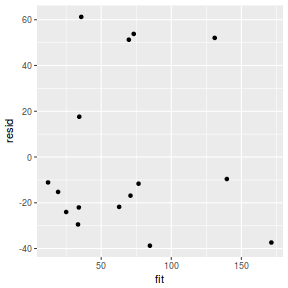
ggplot() + geom_point(data = NULL, aes(y = resid, x = christ$RIPDENS))
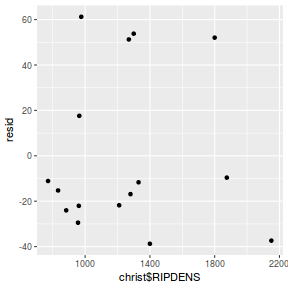
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
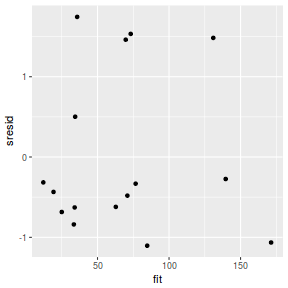
christ.mcmc = christ.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta", "sigma")] # generate a model matrix Xmat = model.matrix(~RIPDENS, christ) ## get median parameter estimates coefs = christ.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(christ.mcmc), function(i) rnorm(nrow(christ), fit[i, ], christ.mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = christ, aes(x = CWDBASAL, fill = "Obs"), alpha = 0.5)
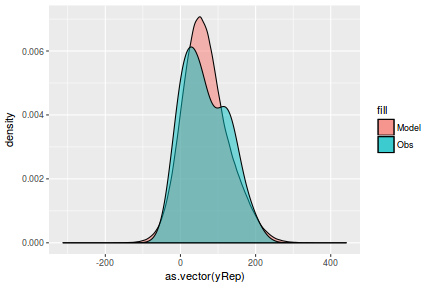
christ.mcmc = christ.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta", "sigma")] # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) fit = apply(fit, 2, function(x) rnorm(length(x), x, christ.mcmc[, "sigma"])) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
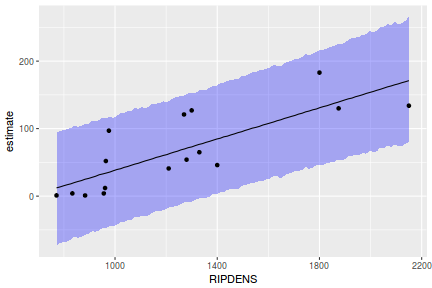
christ.mcmc = christ.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta", "sigma")] # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
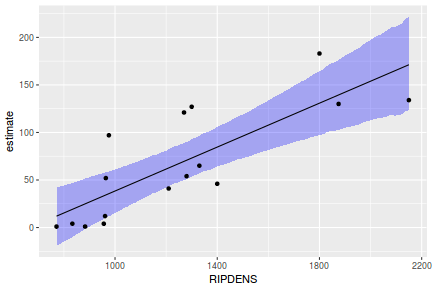 Show RSTAN code
Show RSTAN codelibrary(rstan) christ.mcmc = as.matrix(christ.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(RIPDENS = christ$RIPDENS) Xmat = model.matrix(~RIPDENS, newdata) ## get median parameter estimates coefs = apply(christ.mcmc, 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = christ$CWDBASAL - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
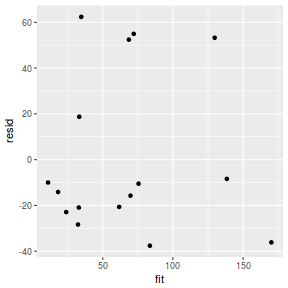
ggplot() + geom_point(data = NULL, aes(y = resid, x = christ$RIPDENS))
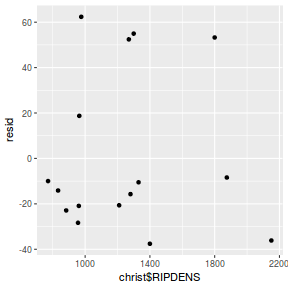
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
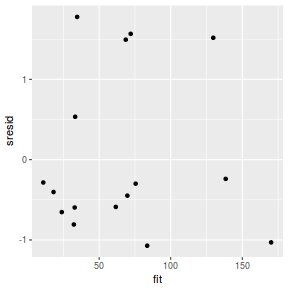
christ.mcmc = as.matrix(christ.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix Xmat = model.matrix(~RIPDENS, christ) ## get median parameter estimates coefs = christ.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(christ.mcmc), function(i) rnorm(nrow(christ), fit[i, ], christ.mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(yRep), fill = "Model"), alpha = 0.5) + geom_density(data = christ, aes(x = CWDBASAL, fill = "Obs"), alpha = 0.5)
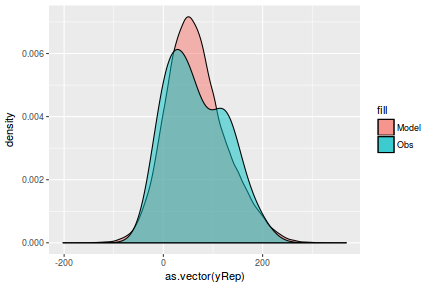
christ.mcmc = as.matrix(christ.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) fit = apply(fit, 2, function(x) rnorm(length(x), x, christ.mcmc[, "sigma"])) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
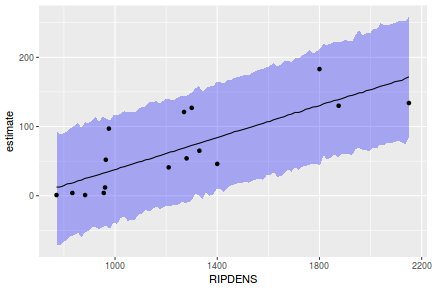
christ.mcmc = as.matrix(christ.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
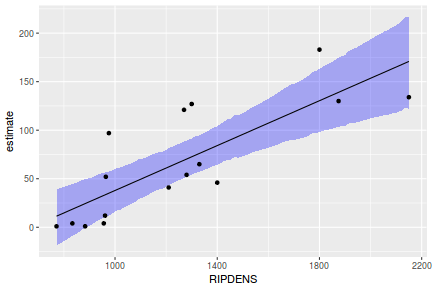 Show RSTANARM code
Show RSTANARM codelibrary(rstanarm) resid = resid(christ.rstanarm) fit = fitted(christ.rstanarm) ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
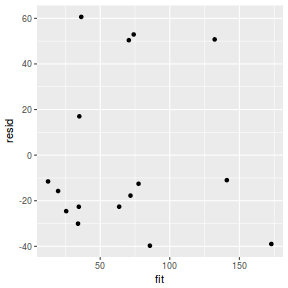
ggplot() + geom_point(data = NULL, aes(y = resid, x = christ$RIPDENS))
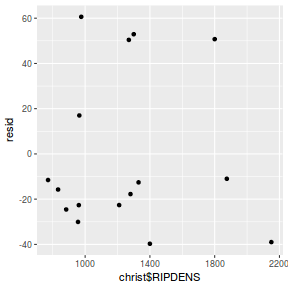
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
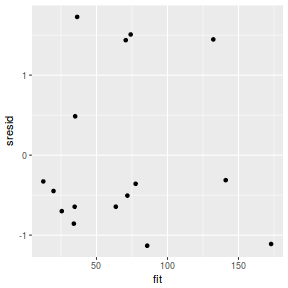
y_pred = posterior_predict(christ.rstanarm) newdata = christ %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -CWDBASAL, -RIPDENS, -LAKE) ggplot(newdata, aes(Value, x = RIPDENS)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = christ, aes(y = CWDBASAL, x = RIPDENS), fill = "red", color = "red", alpha = 0.5)
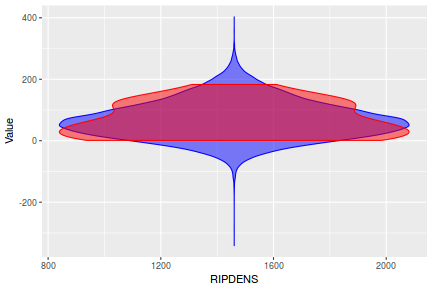
## Calculate the fitted values newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 1000)) fit = posterior_predict(christ.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("CWDBASAL") + scale_x_continuous("RIPDENS") + theme_classic()
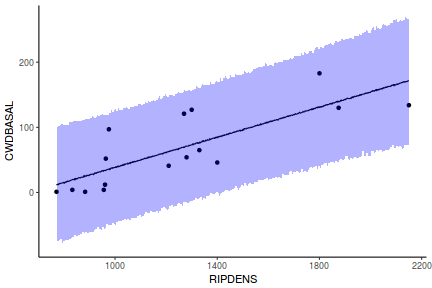
## Marginal plots pp_check(christ.rstanarm, x = christ$RIPDENS, plotfun = "ribbon")
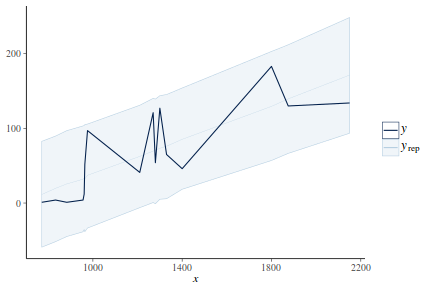
newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = posterior_linpred(christ.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
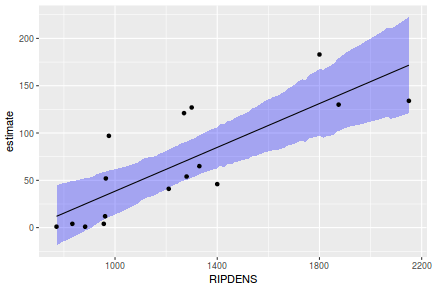 Show BRMS code
Show BRMS codelibrary(brms) resid = resid(christ.brm)[, "Estimate"] fit = fitted(christ.brm)[, "Estimate"] ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
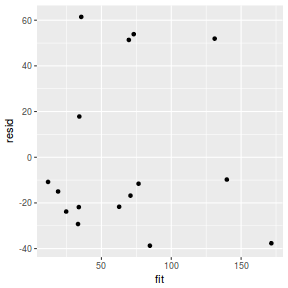
ggplot() + geom_point(data = NULL, aes(y = resid, x = christ$RIPDENS))
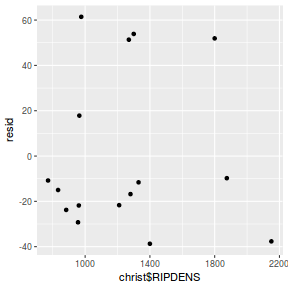
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
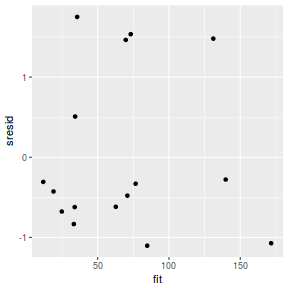
y_pred = posterior_predict(christ.brm) newdata = christ %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -CWDBASAL, -RIPDENS, -LAKE) ggplot(newdata, aes(Value, x = RIPDENS)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = christ, aes(y = CWDBASAL, x = RIPDENS), fill = "red", color = "red", alpha = 0.5)
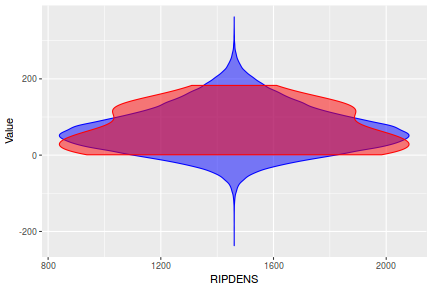
## Calculate the fitted values newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 1000)) fit = posterior_predict(christ.brm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("CWDBASAL") + scale_x_continuous("RIPDENS") + theme_classic()
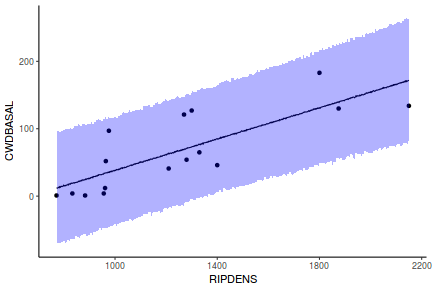
# marginal effects plots marginal_effects(christ.brm)
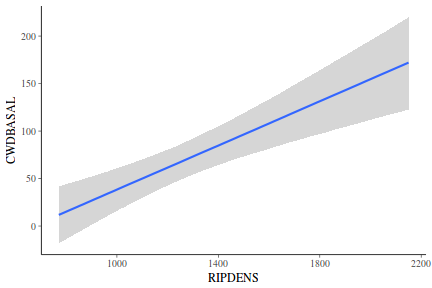
marginal_effects(christ.brm, spaghetti = TRUE, nsamples = 100)
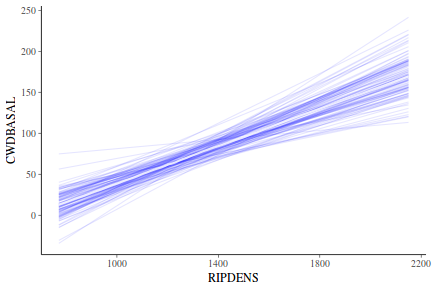
- fit the model against a distribution (family) that more suitably reflects the underlying data generation process. A Gamma and log-normal distributions are two possible candidates. This option will be explored in Tutorial 10.4 and Tutorial 10.7a.
- apply a scale transform on the response (CWDBASAL) such that back-transformed derivations of parameter estimates are naturally bound at zero.
Of course, with this if we transform the scale of the response variable, it might be necessary to similarly rescale the predictor variable
in order to preserve linearity.
Log transformations can be useful when applied to positive responses. In this case however, log transformations result in substantial non-linearity and are therefore not appropriate. Square-root transformations are traditionally popular for normalization, yet can have substantial back-transformation issues when the values to be back-transformed have a mixture of positive and negative values or even a mixture of values less than or greater than one. This can be partly elevated by applying transformations involving the reciprocal of an odd positive integer (powers 1/3, 1/5, 1/7, etc.). Fortunately in this case a square-root transformation appears to be free of such issues.
Although this approach might now be considered less preferred the the previous option, it can be applied within the current (OLS) context and thus will be the approach demonstrated here. -
Re-fit the appropriate Bayesian model.
Show MCMCpack code
library(MCMCpack) christ.mcmcpack = MCMCregress(I(CWDBASAL^(1/3)) ~ RIPDENS, data = christ)
## Check marginal plot christ.mcmc = as.matrix(christ.mcmcpack) # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line()
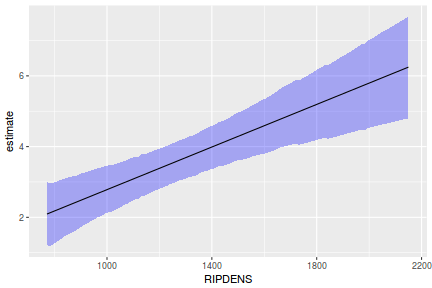
## Check marginal plot newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit^3), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
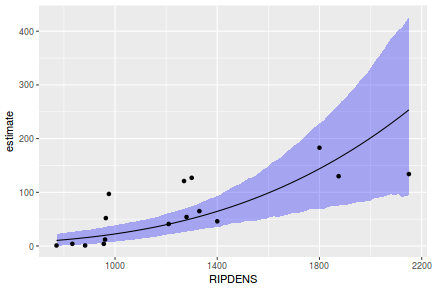 Show JAGS code
Show JAGS codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha+beta*x[i] } #Priors alpha ~ dnorm (0.01,1.0E-6) beta ~ dnorm(0,1.0E-6) tau <- 1 / (sigma * sigma) sigma~dgamma(0.001,0.001) } " christ.list <- with(christ, list(x=RIPDENS, y=CWDBASAL^(1/3),n=nrow(christ)) ) params <- c("alpha","beta","sigma") burnInSteps = 2000 nChains = 3 numSavedSteps = 50000 thinSteps = 10 nIter = ceiling((numSavedSteps * thinSteps)/nChains) christ.r2jags <- jags(data=christ.list, inits=NULL, #or inits=list(inits,inits,inits) # since there are three chains parameters.to.save=params, model.file=textConnection(modelString), n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph information: Observed stochastic nodes: 16 Unobserved stochastic nodes: 3 Total graph size: 77 Initializing model
## Check marginal plot christ.mcmc = christ.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta", "sigma")] # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line()
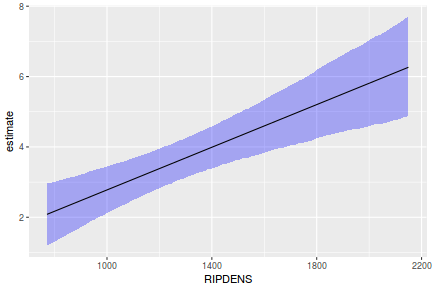
## Check marginal plot newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit^3), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
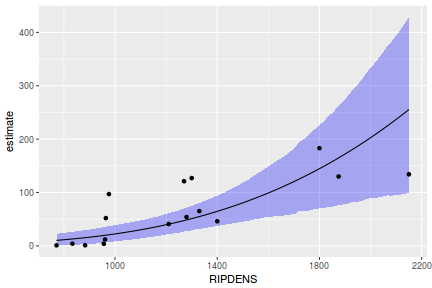 Show RSTAN code
Show RSTAN codemodelString = " data { int<lower=1> n; // total number of observations vector[n] Y; // response variable int<lower=1> nX; // number of effects matrix[n, nX] X; // model matrix } ransformed data { matrix[n, nX - 1] Xc; // centered version of X vector[nX - 1] means_X; // column means of X before centering for (i in 2:nX) { means_X[i - 1] = mean(X[, i]); Xc[, i - 1] = X[, i] - means_X[i - 1]; } } parameters { vector[nX-1] beta; // population-level effects real cbeta0; // center-scale intercept real<lower=0> sigma; // residual SD } ransformed parameters { } model { vector[n] mu; mu = Xc * beta + cbeta0; // prior specifications beta ~ normal(0, 100); cbeta0 ~ normal(0, 100); sigma ~ cauchy(0, 5); // likelihood contribution Y ~ normal(mu, sigma); } generated quantities { real beta0; // population-level intercept beta0 = cbeta0 - dot_product(means_X, beta); } " Xmat <- model.matrix(~RIPDENS, data = christ) christ.list <- with(christ, list(Y = CWDBASAL^(1/3), X = Xmat, nX = ncol(Xmat), n = nrow(christ))) library(rstan) christ.rstan <- stan(data = christ.list, model_code = modelString, chains = 3, iter = 5000, warmup = 500, thin = 2)
SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 1). Gradient evaluation took 1.1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.095137 seconds (Warm-up) 0.176843 seconds (Sampling) 0.27198 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 2). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.103326 seconds (Warm-up) 0.15283 seconds (Sampling) 0.256156 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 3). Gradient evaluation took 6e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.058992 seconds (Warm-up) 0.193731 seconds (Sampling) 0.252723 seconds (Total)## Check marginal plot christ.mcmc = as.matrix(christ.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix newdata = with(christ, data.frame(RIPDENS = seq(min(RIPDENS, na.rm = TRUE), max(RIPDENS, na.rm = TRUE), len = 100))) Xmat = model.matrix(~RIPDENS, data = newdata) ## get median parameter estimates coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line()
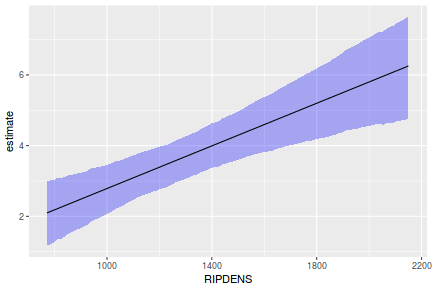
## Check marginal plot newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit^3), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
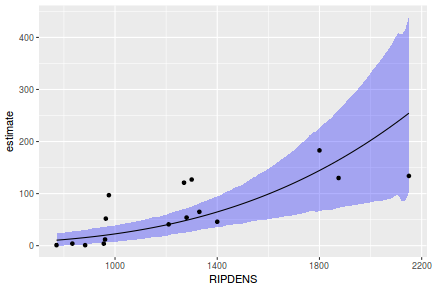 Show RSTANARM code
Show RSTANARM codechrist.rstanarm = stan_glm(I(CWDBASAL^(1/3)) ~ RIPDENS, data = christ, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior_intercept = normal(0, 1000), prior = normal(0, 1000), prior_aux = cauchy(0, 25))
Gradient evaluation took 2.9e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.29 seconds. Adjust your expectations accordingly! Elapsed Time: 0.446307 seconds (Warm-up) 1.05851 seconds (Sampling) 1.50481 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 0.918382 seconds (Warm-up) 1.02339 seconds (Sampling) 1.94177 seconds (Total) Gradient evaluation took 9e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds. Adjust your expectations accordingly! Elapsed Time: 0.508515 seconds (Warm-up) 0.902821 seconds (Sampling) 1.41134 seconds (Total)## Check marginal plot newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = posterior_linpred(christ.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line()
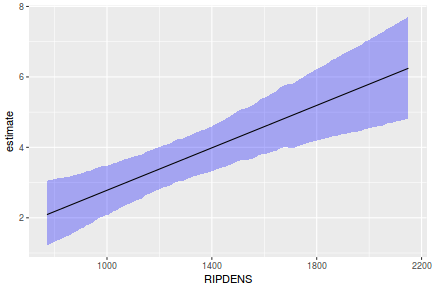
## Check marginal plot newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = posterior_linpred(christ.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit^3), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
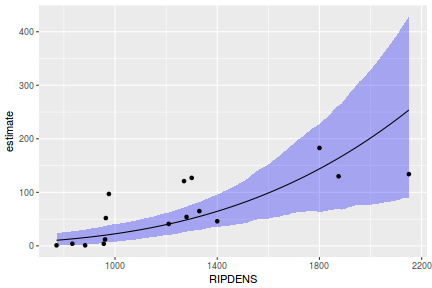 Show BRMS code
Show BRMS codechrist.brm = brm(I(CWDBASAL^(1/3)) ~ RIPDENS, data = christ, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior = c(prior(normal(0, 1000), class = "Intercept"), prior(normal(0, 1000), class = "b"), prior(cauchy(0, 25), class = "sigma")))
Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Elapsed Time: 0.095796 seconds (Warm-up) 0.206029 seconds (Sampling) 0.301825 seconds (Total) Gradient evaluation took 4e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds. Adjust your expectations accordingly! Elapsed Time: 0.109704 seconds (Warm-up) 0.179808 seconds (Sampling) 0.289512 seconds (Total) Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Elapsed Time: 0.095171 seconds (Warm-up) 0.170215 seconds (Sampling) 0.265386 seconds (Total)## Check marginal plot library(brms) christ.mcmc = as.matrix(christ.brm) newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("b_Intercept", "b_RIPDENS")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line()
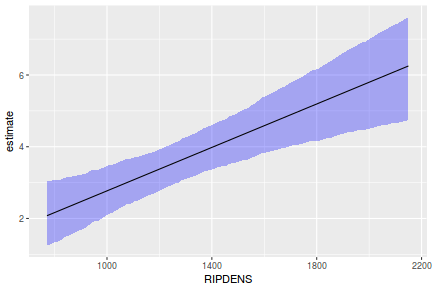
## Check marginal plot newdata = data.frame(RIPDENS = seq(min(christ$RIPDENS, na.rm = TRUE), max(christ$RIPDENS, na.rm = TRUE), len = 100)) fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit^3), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = christ, aes(y = CWDBASAL))
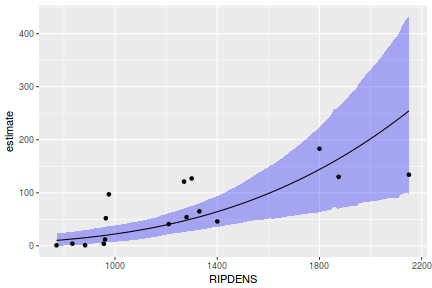
- Explore parameter estimates
Show MCMCpack code
library(MCMCpack) summary(christ.mcmcpack)
Iterations = 1001:11000 Thinning interval = 1 Number of chains = 1 Sample size per chain = 10000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE (Intercept) -0.228718 0.9582329 9.582e-03 9.425e-03 RIPDENS 0.003012 0.0007352 7.352e-06 7.163e-06 sigma2 1.273452 0.5866810 5.867e-03 6.777e-03 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% (Intercept) -2.102296 -0.833106 -0.224161 0.373343 1.706202 RIPDENS 0.001535 0.002556 0.003016 0.003477 0.004467 sigma2 0.586059 0.885812 1.140838 1.495254 2.712343library(broom) tidyMCMC(christ.mcmcpack, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 (Intercept) -0.228718049 0.9582329153 -2.231431354 1.551137800 2 RIPDENS 0.003011873 0.0007351707 0.001520431 0.004435215 3 sigma2 1.273451645 0.5866810241 0.458135477 2.372467015
mcmcpvalue(christ.mcmcpack[, 2])
[1] 6e-04
Show JAGS codelibrary(R2jags) print(christ.r2jags)
Inference for Bugs model at "5", fit using jags, 3 chains, each with 166667 iterations (first 2000 discarded), n.thin = 10 n.sims = 49401 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff alpha -0.254 0.949 -2.133 -0.862 -0.261 0.360 1.634 1.001 41000 beta 0.003 0.001 0.002 0.003 0.003 0.004 0.004 1.001 40000 sigma 1.099 0.227 0.761 0.939 1.064 1.219 1.641 1.001 41000 deviance 47.856 2.709 44.789 45.874 47.154 49.077 54.835 1.001 44000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 3.7 and DIC = 51.5 DIC is an estimate of expected predictive error (lower deviance is better).# OR library(broom) tidyMCMC(as.mcmc(christ.r2jags), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 alpha -0.253735823 0.9488442000 -2.068999951 1.689707623 2 beta 0.003031594 0.0007271712 0.001568172 0.004444404 3 deviance 47.855954540 2.7086335019 44.550776097 53.182854749 4 sigma 1.099085426 0.2270903406 0.708150821 1.543613473
mcmcpvalue(christ.r2jags$BUGSoutput$sims.matrix[, c("beta")])
[1] 0.0006072752
Show RSTAN codelibrary(rstan) summary(christ.rstan)
$summary mean se_mean sd 2.5% 25% 50% 75% beta[1] 0.003014071 9.323866e-06 0.0007442382 0.001574644 0.002529798 0.003005116 0.00349233 cbeta0 3.532588489 4.738430e-03 0.2951544668 2.940823361 3.346518520 3.527742075 3.72151151 sigma 1.145761103 4.002948e-03 0.2497957989 0.778028939 0.971382847 1.107608861 1.27303908 beta0 -0.227276640 1.247551e-02 0.9771620195 -2.205902973 -0.860914613 -0.225280924 0.40455504 lp__ -9.294257523 2.439312e-02 1.3986959429 -12.939374565 -9.884172951 -8.919922970 -8.29386968 97.5% n_eff Rhat beta[1] 0.004529292 6371.357 0.9999844 cbeta0 4.138645318 3879.983 1.0001253 sigma 1.745191663 3894.130 0.9998791 beta0 1.674706864 6135.032 0.9999353 lp__ -7.738204736 3287.848 1.0001045 $c_summary , , chains = chain:1 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.003012956 0.0007367359 0.001608733 0.002523578 0.00299251 0.003485502 0.00448781 cbeta0 3.532558136 0.2903601379 2.955578580 3.348534442 3.52285785 3.722025361 4.15117917 sigma 1.141081087 0.2417855281 0.789443225 0.973305505 1.10659204 1.261085766 1.69409378 beta0 -0.225916238 0.9727568400 -2.140160038 -0.859500810 -0.23688174 0.404555040 1.69298799 lp__ -9.244647008 1.3985239659 -12.986730744 -9.821343736 -8.83667582 -8.243089368 -7.74575619 , , chains = chain:2 stats parameter mean sd 2.5% 25% 50% 75% beta[1] 0.003002075 0.0007521026 0.001516745 0.002522409 0.002991425 0.003487179 cbeta0 3.531119503 0.2944475789 2.934661291 3.344866805 3.531856505 3.716769700 sigma 1.152116061 0.2593116381 0.776460571 0.969750027 1.107721390 1.288436352 beta0 -0.213782019 0.9841321601 -2.257165263 -0.840676452 -0.199133635 0.429111226 lp__ -9.337607246 1.3990541932 -12.936652302 -9.950410337 -8.948028090 -8.327997074 stats parameter 97.5% beta[1] 0.004515869 cbeta0 4.102494115 sigma 1.795514988 beta0 1.673549856 lp__ -7.744029663 , , chains = chain:3 stats parameter mean sd 2.5% 25% 50% 75% beta[1] 0.003027181 0.0007439147 0.001611204 0.002543634 0.003026013 0.003504629 cbeta0 3.534087829 0.3006878009 2.934047840 3.346518520 3.528847242 3.725248748 sigma 1.144086160 0.2479544783 0.777431920 0.971450043 1.109158218 1.267027411 beta0 -0.242131664 0.9747867359 -2.196939511 -0.881006482 -0.254368706 0.387771868 lp__ -9.300518316 1.3975647779 -12.908641487 -9.883698553 -8.942956401 -8.317176264 stats parameter 97.5% beta[1] 0.004560656 cbeta0 4.161998257 sigma 1.750087140 beta0 1.655714877 lp__ -7.729775020# OR library(broom) tidyMCMC(christ.rstan, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 beta[1] 0.003014071 0.0007442382 0.001502438 0.00444291 2 cbeta0 3.532588489 0.2951544668 2.922534076 4.11412126 3 sigma 1.145761103 0.2497957989 0.705767889 1.61446082 4 beta0 -0.227276640 0.9771620195 -2.063573813 1.76973681
mcmcpvalue(as.matrix(christ.rstan)[, c("beta[1]")])
[1] 0.0004444444
Show RSTANARM codelibrary(rstanarm) summary(christ.rstanarm)
Model Info: function: stan_glm family: gaussian [identity] formula: I(CWDBASAL^(1/3)) ~ RIPDENS algorithm: sampling priors: see help('prior_summary') sample: 6750 (posterior sample size) num obs: 16 Estimates: mean sd 2.5% 25% 50% 75% 97.5% (Intercept) -0.2 1.0 -2.2 -0.9 -0.2 0.4 1.7 RIPDENS 0.0 0.0 0.0 0.0 0.0 0.0 0.0 sigma 1.2 0.2 0.8 1.0 1.1 1.3 1.7 mean_PPD 3.5 0.4 2.7 3.3 3.5 3.8 4.4 log-posterior -38.0 1.3 -41.4 -38.6 -37.6 -37.0 -36.4 Diagnostics: mcse Rhat n_eff (Intercept) 0.0 1.0 6377 RIPDENS 0.0 1.0 6750 sigma 0.0 1.0 3214 mean_PPD 0.0 1.0 4507 log-posterior 0.0 1.0 2884 For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).# OR library(broom) tidyMCMC(christ.rstanarm$stanfit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 (Intercept) -0.23221103 0.986663817 -2.152395184 1.702509933 0.9998255 6377 2 RIPDENS 0.00301297 0.000751395 0.001602318 0.004514023 0.9998705 6750 3 sigma 1.15162654 0.238320455 0.753087990 1.637726073 1.0000491 3214 4 mean_PPD 3.52626377 0.422541405 2.664226108 4.341947036 1.0009874 4507 5 log-posterior -37.96063922 1.341449138 -40.594588810 -36.301106545 1.0002068 2884
mcmcpvalue(as.matrix(christ.rstanarm)[, c("RIPDENS")])
[1] 0.0004444444
posterior_interval(christ.rstanarm, prob = 0.95)
2.5% 97.5% (Intercept) -2.180082961 1.681712664 RIPDENS 0.001534922 0.004479068 sigma 0.791948892 1.720893581
(full = loo(christ.rstanarm))
Computed from 6750 by 16 log-likelihood matrix Estimate SE elpd_loo -25.5 2.0 p_loo 2.4 0.7 looic 51.1 4.1 Pareto k diagnostic values: Count Pct (-Inf, 0.5] (good) 15 93.8% (0.5, 0.7] (ok) 1 6.2% (0.7, 1] (bad) 0 0.0% (1, Inf) (very bad) 0 0.0% All Pareto k estimates are ok (k < 0.7) See help('pareto-k-diagnostic') for details.(reduced = loo(update(christ.rstanarm, formula = . ~ 1)))
Gradient evaluation took 1.9e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.19 seconds. Adjust your expectations accordingly! Elapsed Time: 0.013155 seconds (Warm-up) 0.08746 seconds (Sampling) 0.100615 seconds (Total) Gradient evaluation took 8e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.08 seconds. Adjust your expectations accordingly! Elapsed Time: 0.01065 seconds (Warm-up) 0.096919 seconds (Sampling) 0.107569 seconds (Total) Gradient evaluation took 8e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.08 seconds. Adjust your expectations accordingly! Elapsed Time: 0.011049 seconds (Warm-up) 0.089792 seconds (Sampling) 0.100841 seconds (Total)Computed from 6750 by 16 log-likelihood matrix Estimate SE elpd_loo -31.4 1.8 p_loo 1.4 0.3 looic 62.7 3.5 All Pareto k estimates are good (k < 0.5) See help('pareto-k-diagnostic') for details.par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
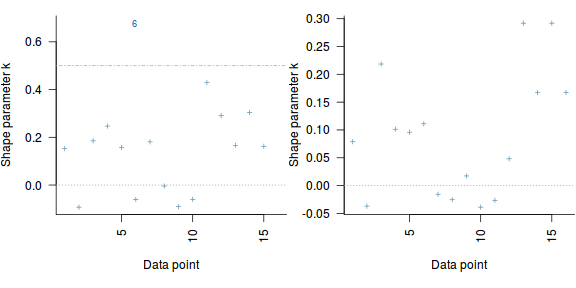
compare_models(full, reduced)
elpd_diff se -5.8 2.3Show BRMS codelibrary(brms) summary(christ.brm)
Family: gaussian(identity) Formula: I(CWDBASAL^(1/3)) ~ RIPDENS Data: christ (Number of observations: 16) Samples: 3 chains, each with iter = 5000; warmup = 500; thin = 2; total post-warmup samples = 6750 ICs: LOO = Not computed; WAIC = Not computed Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept -0.26 0.98 -2.19 1.71 6578 1 RIPDENS 0.00 0.00 0.00 0.00 6750 1 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma 1.14 0.24 0.77 1.71 3962 1 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1).# OR library(broom) tidyMCMC(christ.brm$fit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 b_Intercept -0.256918975 0.9756261920 -2.205145922 1.66121860 1.000152 6578 2 b_RIPDENS 0.003027308 0.0007439753 0.001576751 0.00452126 1.000011 6750 3 sigma 1.139166177 0.2404226588 0.723896152 1.61879905 1.000109 3962
mcmcpvalue(as.matrix(christ.brm)[, c("b_RIPDENS")])
[1] 0.0004444444
posterior_interval(as.matrix(christ.brm), prob = 0.95)
2.5% 97.5% b_Intercept -2.186278649 1.707350799 b_RIPDENS 0.001527964 0.004492076 sigma 0.773711067 1.706181809 lp__ -12.603703660 -7.713089646
(full = loo(christ.brm))
LOOIC SE 51.08 4.22
(reduced = loo(update(christ.brm, formula = . ~ 1)))
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Gradient evaluation took 1.7e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.021586 seconds (Warm-up) 0.035253 seconds (Sampling) 0.056839 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Gradient evaluation took 3e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.022546 seconds (Warm-up) 0.024211 seconds (Sampling) 0.046757 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Gradient evaluation took 6e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.023441 seconds (Warm-up) 0.022783 seconds (Sampling) 0.046224 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Gradient evaluation took 7e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.021962 seconds (Warm-up) 0.034148 seconds (Sampling) 0.05611 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Gradient evaluation took 3e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.025875 seconds (Warm-up) 0.02375 seconds (Sampling) 0.049625 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Gradient evaluation took 4e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.021365 seconds (Warm-up) 0.022538 seconds (Sampling) 0.043903 seconds (Total)LOOIC SE 62.64 3.53
par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
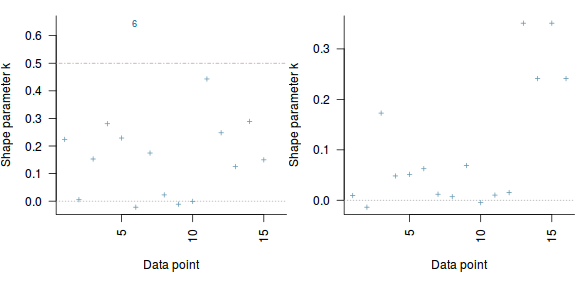
- Generate graphical summaries
Show MCMCpack code
library(MCMCpack) christ.mcmc = christ.mcmcpack ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit^3, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
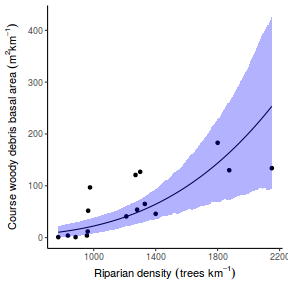
library(MCMCpack) christ.mcmc = christ.mcmcpack ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit^3)) newdata = newdata %>% gather(key = Sample, value = fit, -RIPDENS, -CWDBASAL, -LAKE) newdata.sum = newdata %>% group_by(RIPDENS) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_line(aes(y = fit, x = RIPDENS, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = RIPDENS), color = "blue") + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS), color = "red") + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
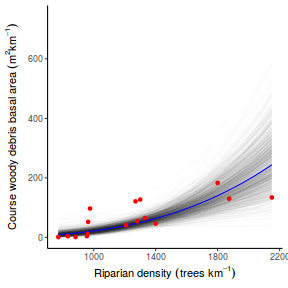 Show JAGS code
Show JAGS codechrist.mcmc = christ.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit^3, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
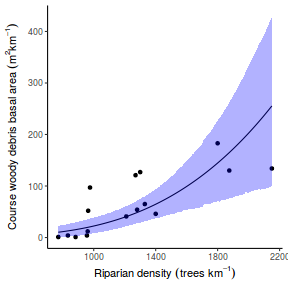
christ.mcmc = christ.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit^3)) newdata = newdata %>% gather(key = Sample, value = fit, -RIPDENS, -CWDBASAL, -LAKE) newdata.sum = newdata %>% group_by(RIPDENS) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_line(aes(y = fit, x = RIPDENS, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = RIPDENS), color = "blue") + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS), color = "red") + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
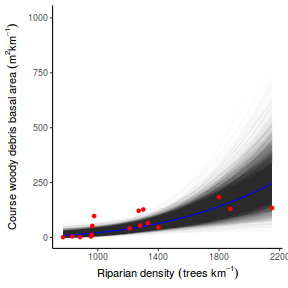 Show RSTAN code
Show RSTAN codechrist.mcmc = as.matrix(christ.rstan) ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(fit^3, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
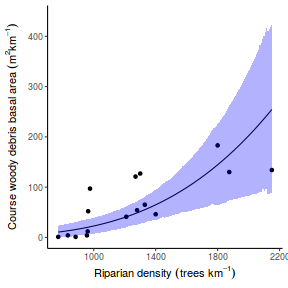
christ.mcmc = as.matrix(christ.rstan) ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit^3)) newdata = newdata %>% gather(key = Sample, value = fit, -RIPDENS, -CWDBASAL, -LAKE) newdata.sum = newdata %>% group_by(RIPDENS) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_line(aes(y = fit, x = RIPDENS, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = RIPDENS), color = "blue") + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS), color = "red") + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
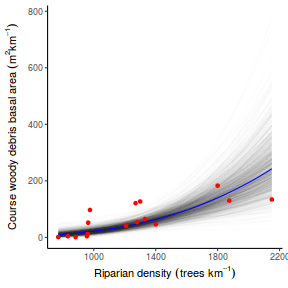 Show RSTANARM code
Show RSTANARM codenewdata = newdata = new_data(christ, seq = "RIPDENS", length = 1000) fit = posterior_linpred(christ.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(fit^3), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
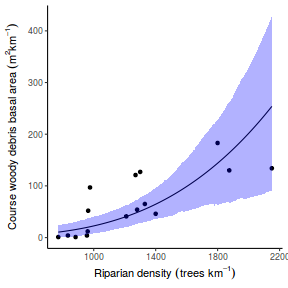
library(rstanarm) christ.mcmc = as.matrix(christ.rstanarm) ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit^3)) newdata = newdata %>% gather(key = Sample, value = fit, -RIPDENS, -CWDBASAL, -LAKE) newdata.sum = newdata %>% group_by(RIPDENS) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_line(aes(y = fit, x = RIPDENS, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = RIPDENS), color = "blue") + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS), color = "red") + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
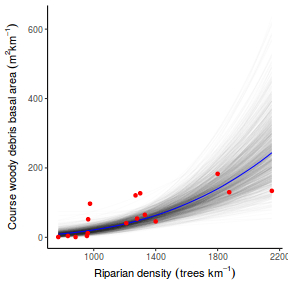 Show BRMS code
Show BRMS codenewdata = marginal_effects(christ.brm)$RIPDENS newdata = newdata %>% mutate_at(vars(estimate__, lower__, upper__), function(x) x^3) ggplot(newdata, aes(y = estimate__, x = RIPDENS)) + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS)) + geom_line() + geom_ribbon(aes(ymin = lower__, ymax = upper__), fill = "blue", alpha = 0.3) + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
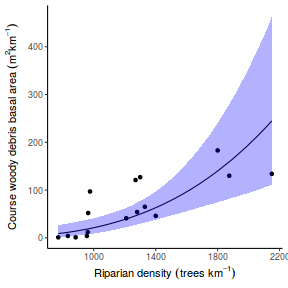
library(brms) christ.mcmc = as.matrix(christ.brm) ## Calculate the fitted values library(newdata) newdata = new_data(christ, seq = "RIPDENS", length = 1000) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("b_Intercept", "b_RIPDENS")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(fit^3)) newdata = newdata %>% gather(key = Sample, value = fit, -RIPDENS, -CWDBASAL, -LAKE) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) newdata.sum = newdata %>% group_by(RIPDENS) %>% dplyr:::summarize(fit = median(fit)) ggplot(newdata, aes(y = estimate, x = RIPDENS)) + geom_line(aes(y = fit, x = RIPDENS, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = RIPDENS), color = "blue") + geom_point(data = christ, aes(y = CWDBASAL, x = RIPDENS), color = "red") + scale_y_continuous(expression(Course ~ woody ~ debris ~ basal ~ area ~ (m^{ 2 } * km^{ -1 }))) + scale_x_continuous(expression(Riparian ~ density ~ (trees ~ km^{ -1 }))) + theme_classic()
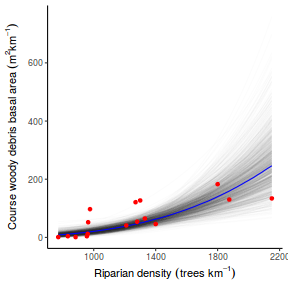
- Explore effect sizes. Lets base this on a reduction of riparian tree density from 1800 trees per km to 900 (ie. a 50% reduction)
Show MCMCpack code
library(MCMCpack) christ.mcmc = christ.mcmcpack newdata = data.frame(RIPDENS = c(1800, 900)) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = (coefs %*% t(Xmat))^3 ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -127.4968 42.52612 -212.4415 -47.65457
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/sqrt(christ.mcmc[, "sigma2"]) (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -120.0312 44.01978 -207.1585 -36.38872
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -87.16801 23.84596 -98.37591 -72.94357
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9987
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.1283199 0.2384596 0.01624085 0.2705643
Show JAGS codechrist.mcmc = christ.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values library(newdata) newdata = data.frame(RIPDENS = c(1800, 900)) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("alpha", "beta")] fit = (coefs %*% t(Xmat))^3 ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -128.4078 42.24404 -213.3121 -50.28397
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/christ.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -121.2396 43.60707 -208.0248 -40.2417
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -87.62622 7.670893 -98.39554 -73.21562
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.999413
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.1237378 0.07670893 0.01604456 0.2678438
Show RSTAN codechrist.mcmc = as.matrix(christ.rstan) ## Calculate the fitted values library(newdata) newdata = data.frame(RIPDENS = c(1800, 900)) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("beta0", "beta[1]")] fit = (coefs %*% t(Xmat))^3 ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -127.901 43.49555 -212.4069 -47.67477
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/christ.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -115.8683 42.19086 -197.3489 -36.80674
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -87.35891 7.959909 -98.88673 -72.67531
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.998963
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.1264109 0.07959909 0.0111327 0.2732469
Show RSTANARM codechrist.mcmc = as.matrix(christ.rstanarm) ## Calculate the fitted values library(newdata) newdata = data.frame(RIPDENS = c(1800, 900)) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = (coefs %*% t(Xmat))^3 ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -127.5175 43.52311 -211.7174 -42.58836
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/christ.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -115.1682 43.20934 -199.9961 -33.38101
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -87.31871 8.666773 -98.73333 -73.0458
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.998963
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.1268129 0.08666773 0.01266668 0.269542
Show BRMS codechrist.mcmc = as.matrix(christ.brm) ## Calculate the fitted values library(newdata) newdata = data.frame(RIPDENS = c(1800, 900)) Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("b_Intercept", "b_RIPDENS")] fit = (coefs %*% t(Xmat))^3 ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -127.7564 43.13748 -213.7665 -46.06526
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/christ.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -116.5389 42.97048 -198.0587 -34.77462
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 -87.56004 7.863212 -98.95192 -73.06729
# Probability that the effect is greater than 25% (a decline of >25%) sum(-1 * ESp > 25)/length(ESp)
[1] 0.9994074
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 0.1243996 0.07863212 0.01048081 0.2693271
- Finite-population standard deviations
Show MCMCpack code
library(MCMCpack) christ.mcmc = christ.mcmcpack newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = (coefs %*% t(Xmat))^3 resid = sweep(fit, 2, christ$CWDBASAL, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$RIPDENS[2] - newdata$RIPDENS[1])) * sd(christ$RIPDENS) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 44.74318 13.15610 20.33927 71.74818 2 sd.resid 52.61889 15.60157 37.67623 82.38526
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 46.76942 4.854287 36.97993 52.52833 2 sd.resid 53.23058 4.854287 47.47167 63.02007
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
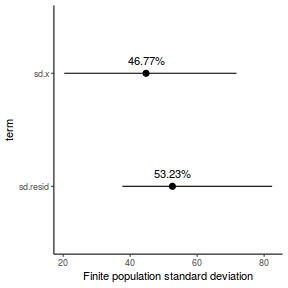 Show JAGS code
Show JAGS codechrist.mcmc = christ.r2jags$BUGSoutput$sims.matrix newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("alpha", "beta")] fit = (coefs %*% t(Xmat))^3 resid = sweep(fit, 2, christ$CWDBASAL, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$RIPDENS[2] - newdata$RIPDENS[1])) * sd(christ$RIPDENS) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 44.99259 12.98809 21.03171 71.76557 2 sd.resid 52.86000 15.79693 38.00992 83.79307
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 46.69376 4.475378 37.24855 52.39210 2 sd.resid 53.30624 4.475378 47.60790 62.75145
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
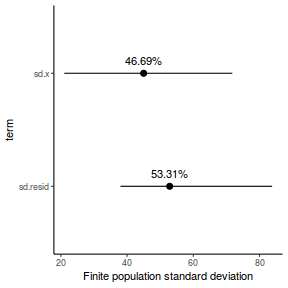 Show RSTAN code
Show RSTAN codechrist.mcmc = as.matrix(christ.rstan) newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("beta0", "beta[1]")] fit = (coefs %*% t(Xmat))^3 resid = sweep(fit, 2, christ$CWDBASAL, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$RIPDENS[2] - newdata$RIPDENS[1])) * sd(christ$RIPDENS) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 44.85837 13.43119 19.73555 70.9123 2 sd.resid 52.82636 16.39363 37.84590 84.4382
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 46.72086 4.700478 36.52322 52.45014 2 sd.resid 53.27914 4.700478 47.54986 63.47678
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
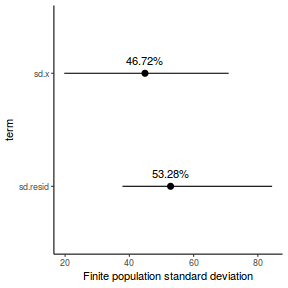 Show RSTANARM code
Show RSTANARM codechrist.mcmc = as.matrix(christ.rstanarm) newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = (coefs %*% t(Xmat))^3 resid = sweep(fit, 2, christ$CWDBASAL, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$RIPDENS[2] - newdata$RIPDENS[1])) * sd(christ$RIPDENS) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 44.70379 13.48680 17.81688 71.65064 2 sd.resid 52.85626 15.96105 37.88927 84.56797
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 46.64012 4.871145 36.17485 52.36926 2 sd.resid 53.35988 4.871145 47.63074 63.82515
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
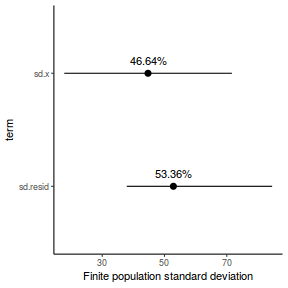 Show BRMS code
Show BRMS codechrist.mcmc = as.matrix(christ.brm) newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("b_Intercept", "b_RIPDENS")] fit = (coefs %*% t(Xmat))^3 resid = sweep(fit, 2, christ$CWDBASAL, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$RIPDENS[2] - newdata$RIPDENS[1])) * sd(christ$RIPDENS) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 44.7194 13.31368 18.65857 70.60969 2 sd.resid 52.8973 16.02284 37.75326 84.87694
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 46.53784 4.664826 36.44587 52.75618 2 sd.resid 53.46216 4.664826 47.24382 63.55413
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
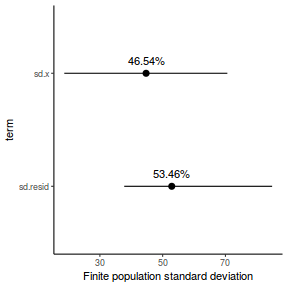
- $R^2$
Show MCMCpack code
library(MCMCpack) christ.mcmc = christ.mcmcpack newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = (coefs %*% t(Xmat)) x = christ$CWDBASAL^(1/3) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.5568242 0.1266604 0.3009179 0.709935
# for comparison summary(lm(I(CWDBASAL^(1/3)) ~ RIPDENS, data = christ))
Call: lm(formula = I(CWDBASAL^(1/3)) ~ RIPDENS, data = christ) Residuals: Min 1Q Median 3Q Max -1.4269 -0.7813 -0.1634 0.6242 1.8866 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.2420810 0.8770701 -0.276 0.786572 RIPDENS 0.0030227 0.0006715 4.502 0.000498 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1.041 on 14 degrees of freedom Multiple R-squared: 0.5914, Adjusted R-squared: 0.5622 F-statistic: 20.27 on 1 and 14 DF, p-value: 0.0004976Show JAGS codechrist.mcmc = christ.r2jags$BUGSoutput$sims.matrix newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("alpha", "beta")] fit = (coefs %*% t(Xmat)) x = christ$CWDBASAL^(1/3) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.5599356 0.1236288 0.3045365 0.7099365
Show RSTAN codechrist.mcmc = as.matrix(christ.rstan) newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("beta0", "beta[1]")] fit = (coefs %*% t(Xmat)) x = christ$CWDBASAL^(1/3) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.5558864 0.1264171 0.2944248 0.7099365
Show RSTANARM codechrist.mcmc = as.matrix(christ.rstanarm) newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("(Intercept)", "RIPDENS")] fit = (coefs %*% t(Xmat)) x = christ$CWDBASAL^(1/3) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.5553571 0.1285036 0.2933517 0.7099365
Show BRMS codechrist.mcmc = as.matrix(christ.brm) newdata = christ Xmat = model.matrix(~RIPDENS, newdata) coefs = christ.mcmc[, c("b_Intercept", "b_RIPDENS")] fit = (coefs %*% t(Xmat)) x = christ$CWDBASAL^(1/3) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.5579719 0.1268644 0.2976436 0.7099361
The value of plotting the fitted model is evident at the point. Whilst the prediction intervals did encompass all the observed data, suggesting that the model does represent the observed data, the fact that prediction or confidence intervals descend below zero for low values of RIPDENS indicates that the model does not adequately capture the underlying data generation process. Obviously, it is not logically possible to obtain a basal area of course woody debris less than zero.
At this point we should make adjustments to correct this. There are multiple options available:
Clearly, whilst not perfect, the effects plot is more logical. Fitted values (and confidence intervals) on the third root scale do not contain a mixture of values above and below zero and thus, back-transformations to a natural scale are sensible.
Simple linear regression
Here is a modified example from Quinn and Keough (2002). Peake & Quinn (1993) investigated the relationship between the number of individuals of invertebrates living in amongst clumps of mussels on a rocky intertidal shore and the area of those mussel clumps.
Download PeakeQuinn data set| Format of peakquinn.csv data files | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||
peakquinn <- read.table("../downloads/data/peakquinn.csv", header = T, sep = ",", strip.white = T) peakquinn
AREA INDIV 1 516.00 18 2 469.06 60 3 462.25 57 4 938.60 100 5 1357.15 48 6 1773.66 118 7 1686.01 148 8 1786.29 214 9 3090.07 225 10 3980.12 283 11 4424.84 380 12 4451.68 278 13 4982.89 338 14 4450.86 274 15 5490.74 569 16 7476.21 509 17 7138.82 682 18 9149.94 600 19 10133.07 978 20 9287.69 363 21 13729.13 1402 22 20300.77 675 23 24712.72 1159 24 27144.03 1062 25 26117.81 632
The relationship between two continuous variables can be analyzed by simple linear regression. As with question 2, note that the levels of the predictor variable were measured, not fixed, and thus parameter estimates should be based on model II RMA regression. Note however, that the hypothesis test for slope is uneffected by whether the predictor variable is fixed or measured.
Before performing the analysis we need to check the assumptions. To evaluate the assumptions of linearity, normality and homogeneity of variance, construct a
scatterplot
ggplot(peakquinn, aes(y = INDIV, x = AREA)) + geom_point() + geom_smooth()
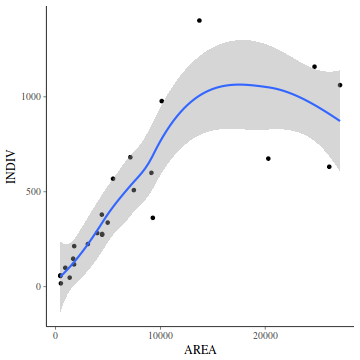
ggplot(peakquinn, aes(y = INDIV, x = 1)) + geom_boxplot()
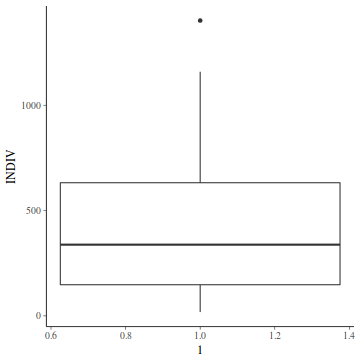
ggplot(peakquinn, aes(y = AREA, x = 1)) + geom_boxplot()
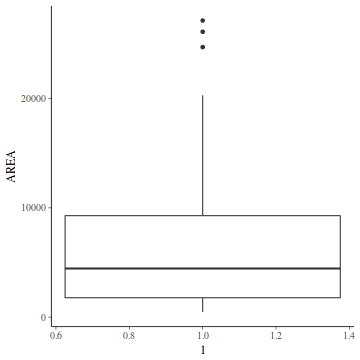
- Consider the assumptions and suitability of the data for simple linear regression:
- In this case, the researchers are interested in investigating whether there is a relationship between the number of invertebrate individuals and mussel clump area as well as generating a predictive model. However, they are not interested in the specific magnitude of the relationship (slope) and have no intension of comparing their slope to any other non-zero values. Is
model I or II regression
appropriate in these circumstances?. Explain?
- Is there any evidence that the other assumptions are likely to be violated?
- In this case, the researchers are interested in investigating whether there is a relationship between the number of invertebrate individuals and mussel clump area as well as generating a predictive model. However, they are not interested in the specific magnitude of the relationship (slope) and have no intension of comparing their slope to any other non-zero values. Is
model I or II regression
appropriate in these circumstances?. Explain?
- There is clear evidence of non-normality and non-linearity. As with the previous example, the most appropriate approach would be to
use a more suitable distribution. Nevertheless, we will reserve such an approach to a later tutorial and instead attempt to satisfy the assumptions via scale transformations
for now. Lets try a log-log transformation of the response and predictor. Mimic this by log transforming the axes during exploratory data analysis.
Show code
ggplot(peakquinn, aes(y = INDIV, x = AREA)) + geom_point() + geom_smooth() + scale_y_log10() + scale_x_log10()
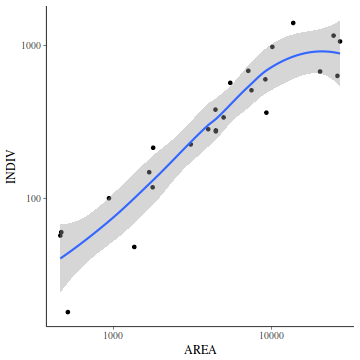
ggplot(peakquinn, aes(y = INDIV, x = 1)) + geom_boxplot() + scale_y_log10()
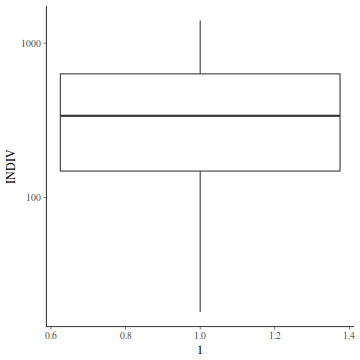
ggplot(peakquinn, aes(y = AREA, x = 1)) + geom_boxplot() + scale_y_log10()
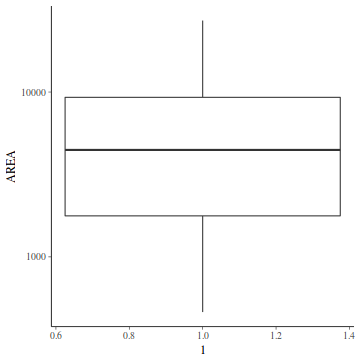
-
Once you are satisfied with the transformations, fit the appropriate Bayesian model.
Show MCMCpack code
library(MCMCpack) peakquinn.mcmcpack = MCMCregress(log10(INDIV) ~ log10(AREA), data = peakquinn)
Show JAGS codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha+beta*x[i] } #Priors alpha ~ dnorm (0.01,1.0E-6) beta ~ dnorm(0,1.0E-6) tau <- 1 / (sigma * sigma) sigma~dgamma(0.001,0.001) } " peakquinn.list <- with(peakquinn, list(x=log10(AREA), y=log10(INDIV),n=nrow(peakquinn)) ) params <- c("alpha","beta","sigma") burnInSteps = 2000 nChains = 3 numSavedSteps = 50000 thinSteps = 10 nIter = ceiling((numSavedSteps * thinSteps)/nChains) peakquinn.r2jags <- jags(data=peakquinn.list, inits=NULL, #or inits=list(inits,inits,inits) # since there are three chains parameters.to.save=params, model.file=textConnection(modelString), #"../downloads/BUGSscripts/tut7.2bQ1_JAGS.txt", n.chains=nChains, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph information: Observed stochastic nodes: 25 Unobserved stochastic nodes: 3 Total graph size: 113 Initializing model
Show RSTAN codemodelString = " data { int<lower=1> n; // total number of observations vector[n] Y; // response variable int<lower=1> nX; // number of effects matrix[n, nX] X; // model matrix } ransformed data { matrix[n, nX - 1] Xc; // centered version of X vector[nX - 1] means_X; // column means of X before centering for (i in 2:nX) { means_X[i - 1] = mean(X[, i]); Xc[, i - 1] = X[, i] - means_X[i - 1]; } } parameters { vector[nX-1] beta; // population-level effects real cbeta0; // center-scale intercept real<lower=0> sigma; // residual SD } ransformed parameters { } model { vector[n] mu; mu = Xc * beta + cbeta0; // prior specifications beta ~ normal(0, 100); cbeta0 ~ normal(0, 100); sigma ~ cauchy(0, 5); // likelihood contribution Y ~ normal(mu, sigma); } generated quantities { real beta0; // population-level intercept beta0 = cbeta0 - dot_product(means_X, beta); } " Xmat <- model.matrix(~log10(AREA), data = peakquinn) peakquinn.list <- with(peakquinn, list(Y = log10(INDIV), X = Xmat, nX = ncol(Xmat), n = nrow(peakquinn))) library(rstan) peakquinn.rstan <- stan(data = peakquinn.list, model_code = modelString, chains = 3, iter = 5000, warmup = 500, thin = 2)
SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 1). Gradient evaluation took 1.6e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.010294 seconds (Warm-up) 0.081637 seconds (Sampling) 0.091931 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 2). Gradient evaluation took 7e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.011199 seconds (Warm-up) 0.100166 seconds (Sampling) 0.111365 seconds (Total) SAMPLING FOR MODEL 'c89e04c2495a0b6eb4be2b406df0876b' NOW (CHAIN 3). Gradient evaluation took 7e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 501 / 5000 [ 10%] (Sampling) Iteration: 1000 / 5000 [ 20%] (Sampling) Iteration: 1500 / 5000 [ 30%] (Sampling) Iteration: 2000 / 5000 [ 40%] (Sampling) Iteration: 2500 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.010724 seconds (Warm-up) 0.079799 seconds (Sampling) 0.090523 seconds (Total)Show RSTANARM codepeakquinn.rstanarm = stan_glm(log10(INDIV) ~ log10(AREA), data = peakquinn, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior_intercept = normal(0, 100), prior = normal(0, 100), prior_aux = cauchy(0, 5))
Gradient evaluation took 2.7e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.27 seconds. Adjust your expectations accordingly! Elapsed Time: 0.111367 seconds (Warm-up) 0.358927 seconds (Sampling) 0.470294 seconds (Total) Gradient evaluation took 1.6e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds. Adjust your expectations accordingly! Elapsed Time: 0.129212 seconds (Warm-up) 0.390084 seconds (Sampling) 0.519296 seconds (Total) Gradient evaluation took 1.1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds. Adjust your expectations accordingly! Elapsed Time: 0.145679 seconds (Warm-up) 0.363303 seconds (Sampling) 0.508982 seconds (Total)Show BRMS codepeakquinn.brm = brm(log10(INDIV) ~ log10(AREA), data = peakquinn, iter = 5000, warmup = 500, chains = 3, thin = 2, refresh = 0, prior = c(prior(normal(0, 100), class = "Intercept"), prior(normal(0, 100), class = "b"), prior(cauchy(0, 5), class = "sigma")))
Gradient evaluation took 1.7e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds. Adjust your expectations accordingly! Elapsed Time: 0.0128 seconds (Warm-up) 0.087363 seconds (Sampling) 0.100163 seconds (Total) Gradient evaluation took 7e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. Adjust your expectations accordingly! Elapsed Time: 0.011621 seconds (Warm-up) 0.099485 seconds (Sampling) 0.111106 seconds (Total) Gradient evaluation took 7e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. Adjust your expectations accordingly! Elapsed Time: 0.010653 seconds (Warm-up) 0.100251 seconds (Sampling) 0.110904 seconds (Total) - Explore MCMC diagnostics
Show MCMCpack code
library(MCMCpack) plot(peakquinn.mcmcpack)
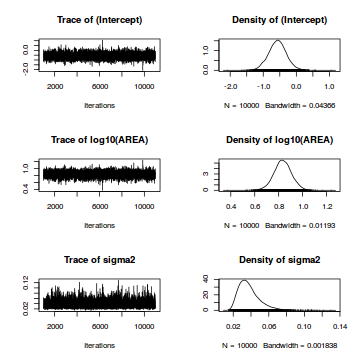
raftery.diag(peakquinn.mcmcpack)
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) (Intercept) 2 3741 3746 0.999 log10(AREA) 2 3962 3746 1.060 sigma2 2 3710 3746 0.990autocorr.diag(peakquinn.mcmcpack)
(Intercept) log10(AREA) sigma2 Lag 0 1.0000000000 1.000000e+00 1.000000000 Lag 1 0.0116532661 9.334020e-03 0.095839414 Lag 5 0.0012783772 3.663530e-03 -0.008301125 Lag 10 0.0003423311 9.355755e-05 0.019264269 Lag 50 -0.0062782335 -6.907045e-03 0.001771369
Show JAGS codelibrary(R2jags) library(coda) peakquinn.mcmc = as.mcmc(peakquinn.r2jags) plot(peakquinn.mcmc)
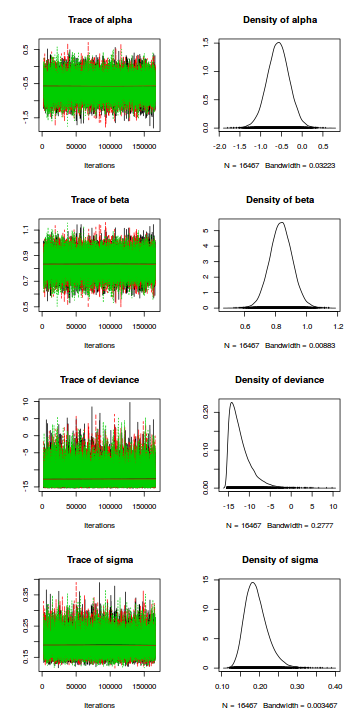
raftery.diag(peakquinn.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 37830 3746 10.10 beta 10 37440 3746 9.99 deviance 10 37440 3746 9.99 sigma 10 37440 3746 9.99 [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 36900 3746 9.85 beta 10 37440 3746 9.99 deviance 20 37830 3746 10.10 sigma 20 37830 3746 10.10 [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 Burn-in Total Lower bound Dependence (M) (N) (Nmin) factor (I) alpha 20 38780 3746 10.40 beta 20 36530 3746 9.75 deviance 20 38400 3746 10.30 sigma 20 36900 3746 9.85autocorr.diag(peakquinn.mcmc)
alpha beta deviance sigma Lag 0 1.0000000000 1.0000000000 1.000000000 1.000000000 Lag 10 0.0001195037 -0.0003816953 -0.001896208 0.005446906 Lag 50 0.0053945316 0.0055864308 -0.007529212 -0.006124288 Lag 100 -0.0033999014 -0.0038914471 0.003445373 0.001132613 Lag 500 -0.0016218704 -0.0022681430 0.003983872 0.003848320
Show RSTAN codelibrary(rstan) library(coda) s = as.array(peakquinn.rstan) peakquinn.mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(peakquinn.mcmc)
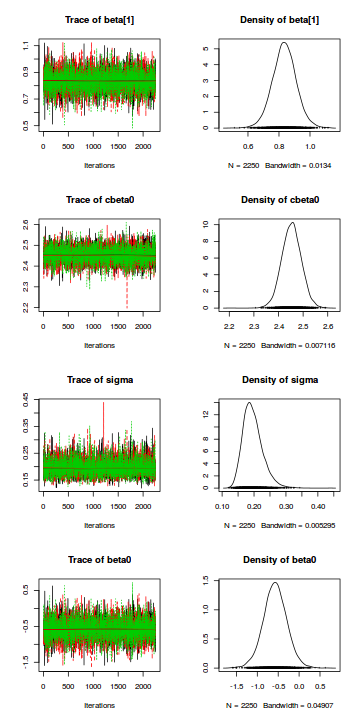
raftery.diag(peakquinn.mcmc)
$`1` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`2` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`3` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(peakquinn.mcmc)
beta[1] cbeta0 sigma beta0 Lag 0 1.000000000 1.0000000000 1.000000000 1.000000000 Lag 1 0.003570983 0.0306426694 0.057421665 0.007040986 Lag 5 -0.011594291 -0.0049307070 -0.004491589 -0.015518655 Lag 10 0.003007244 -0.0305839541 -0.021560119 0.002349694 Lag 50 -0.032332439 0.0002296363 0.015170809 -0.032066086
library(rstan) library(coda) stan_ac(peakquinn.rstan)
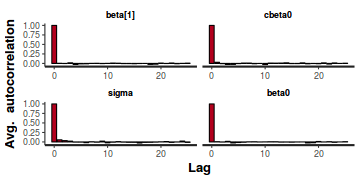
stan_rhat(peakquinn.rstan)
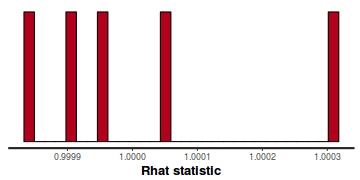
stan_ess(peakquinn.rstan)
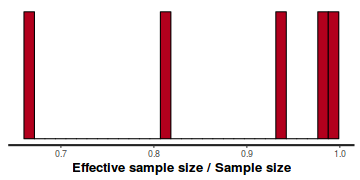
# using Bayeseplot library(bayesplot) detach("package:reshape") mcmc_trace(as.array(peakquinn.rstan))
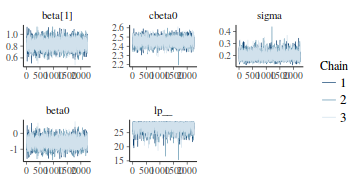
mcmc_trace(as.array(peakquinn.rstan), regex_pars = "beta|sigma")
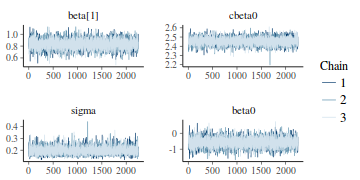
mcmc_dens(as.array(peakquinn.rstan))
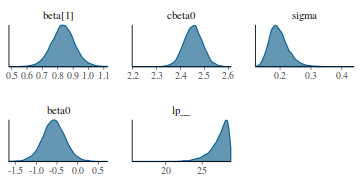
detach("package:reshape") library(bayesplot) mcmc_combo(as.array(peakquinn.rstan))
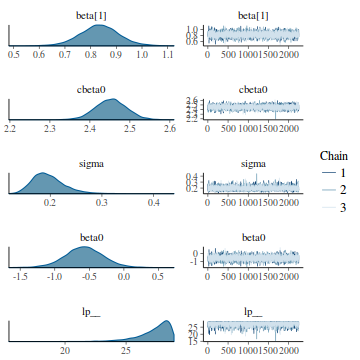 Show RSTANARM code
Show RSTANARM codelibrary(rstan) library(coda) s = as.array(peakquinn.rstanarm) peakquinn.mcmc <- do.call(mcmc.list, plyr:::alply(s[, , -(length(s[1, 1, ]))], 2, as.mcmc)) plot(peakquinn.mcmc)
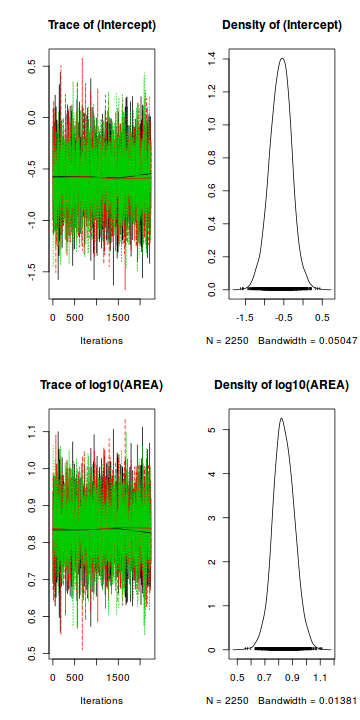
raftery.diag(peakquinn.mcmc)
$`1` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`2` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s $`3` Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(peakquinn.mcmc)
(Intercept) log10(AREA) Lag 0 1.000000000 1.000000000 Lag 1 0.028679084 0.022344878 Lag 5 -0.004308483 -0.007113919 Lag 10 0.009629726 0.010009127 Lag 50 -0.013881750 -0.015410078
library(rstan) library(coda) stan_ac(peakquinn.rstanarm)
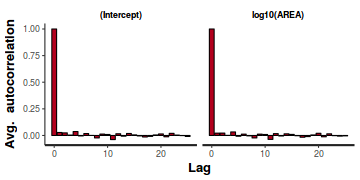
stan_rhat(peakquinn.rstanarm)
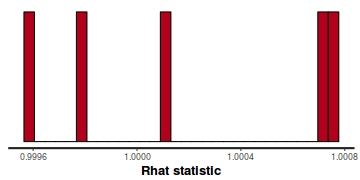
stan_ess(peakquinn.rstanarm)
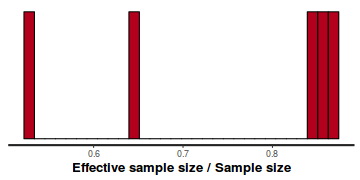
# using Bayeseplot library(bayesplot) detach("package:reshape") mcmc_trace(as.array(peakquinn.rstanarm))
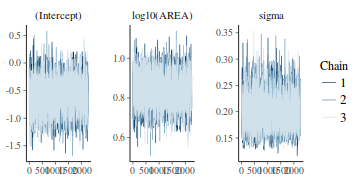
mcmc_trace(as.array(peakquinn.rstanarm), regex_pars = "Intercept|x|sigma")
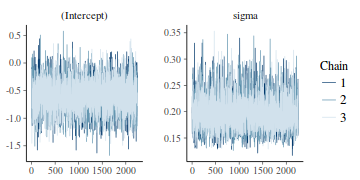
mcmc_dens(as.array(peakquinn.rstan))
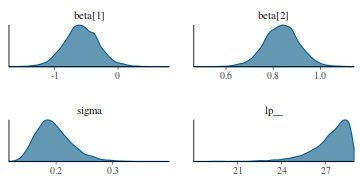
detach("package:reshape") library(bayesplot) mcmc_combo(as.array(peakquinn.rstanarm))
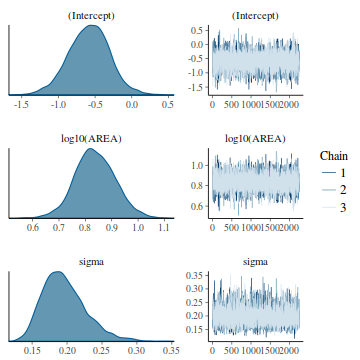
library(rstanarm) posterior_vs_prior(peakquinn.rstanarm, color_by = "vs", group_by = TRUE, facet_args = list(scales = "free_y"))
Gradient evaluation took 3.1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.31 seconds. Adjust your expectations accordingly! Elapsed Time: 0.036027 seconds (Warm-up) 0.04039 seconds (Sampling) 0.076417 seconds (Total) Gradient evaluation took 1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds. Adjust your expectations accordingly! Elapsed Time: 0.050907 seconds (Warm-up) 0.042161 seconds (Sampling) 0.093068 seconds (Total)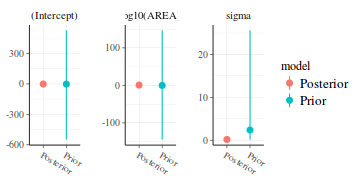 Show BRMS code
Show BRMS codelibrary(coda) library(brms) peakquinn.mcmc = as.mcmc(peakquinn.brm) plot(peakquinn.mcmc)
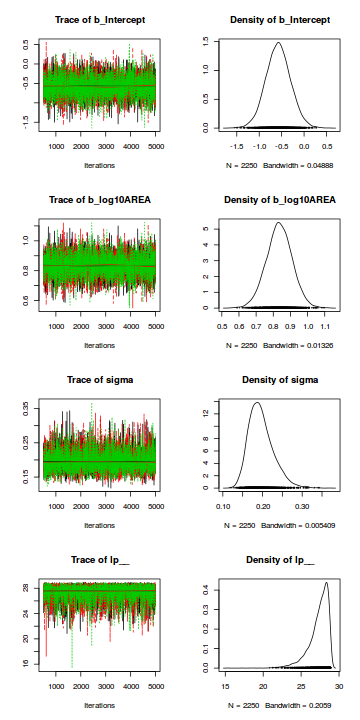
raftery.diag(peakquinn.mcmc)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
autocorr.diag(peakquinn.mcmc)
Error in ts(x, start = start(x), end = end(x), deltat = thin(x)): invalid time series parameters specified
library(coda) stan_ac(peakquinn.brm$fit)
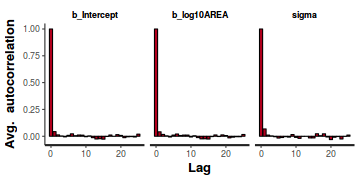
stan_rhat(peakquinn.brm$fit)

stan_ess(peakquinn.brm$fit)
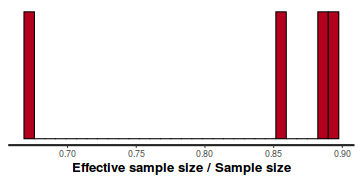
- Perform model validation
Show MCMCpack code
library(MCMCpack) peakquinn.mcmc = as.data.frame(peakquinn.mcmcpack) # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
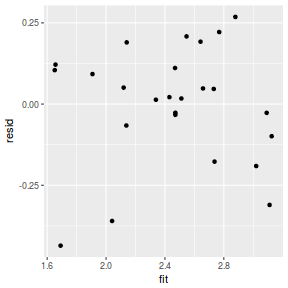
library(MCMCpack) peakquinn.mcmc = as.data.frame(peakquinn.mcmcpack) # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = peakquinn$AREA)) + scale_x_log10()
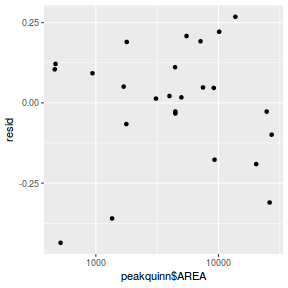
library(MCMCpack) peakquinn.mcmc = as.data.frame(peakquinn.mcmcpack) # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
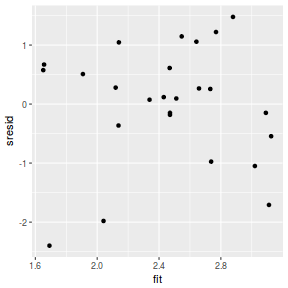
library(MCMCpack) peakquinn.mcmc = as.matrix(peakquinn.mcmcpack) # generate a model matrix Xmat = model.matrix(~log10(AREA), peakquinn) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(peakquinn.mcmc), function(i) rnorm(nrow(peakquinn), fit[i, ], sqrt(peakquinn.mcmc[i, "sigma2"]))) ggplot() + geom_density(data = NULL, aes(x = as.vector(10^yRep), fill = "Model"), alpha = 0.5) + geom_density(data = peakquinn, aes(x = INDIV, fill = "Obs"), alpha = 0.5) + scale_x_log10()
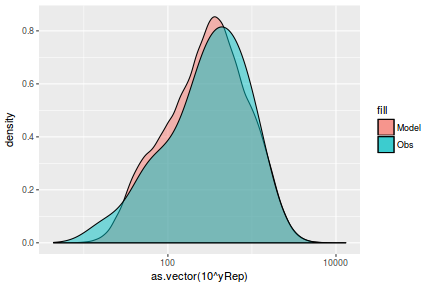
## Plot predicted effects library(MCMCpack) peakquinn.mcmc = as.matrix(peakquinn.mcmcpack) # generate a model matrix newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) Xmat = model.matrix(~log10(AREA), data = newdata) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) fit = apply(fit, 2, function(x) rnorm(length(x), x, sqrt(peakquinn.mcmc[, "sigma2"]))) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
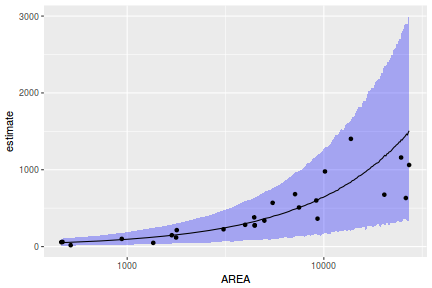
## Plot effects library(MCMCpack) peakquinn.mcmc = as.matrix(peakquinn.mcmcpack) # generate a model matrix newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) Xmat = model.matrix(~log10(AREA), data = newdata) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
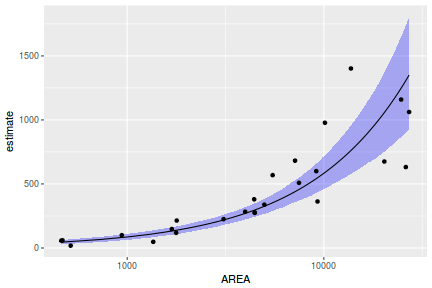 Show JAGS code
Show JAGS codelibrary(R2jags) peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
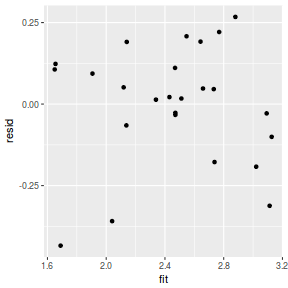
library(R2jags) peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = peakquinn$AREA)) + scale_x_log10()
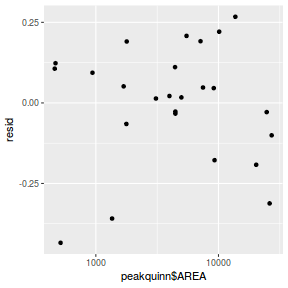
library(R2jags) peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
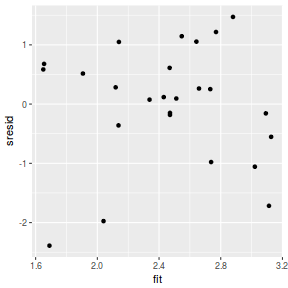
library(R2jags) peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta", "sigma")] # generate a model matrix Xmat = model.matrix(~log10(AREA), peakquinn) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(peakquinn.mcmc), function(i) rnorm(nrow(peakquinn), fit[i, ], peakquinn.mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(10^yRep), fill = "Model"), alpha = 0.5) + geom_density(data = peakquinn, aes(x = INDIV, fill = "Obs"), alpha = 0.5) + scale_x_log10()
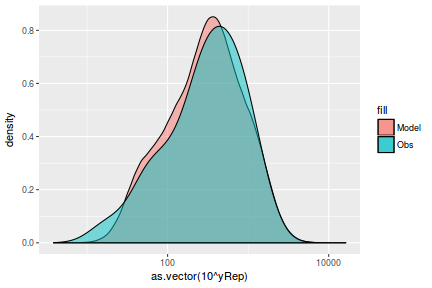
## Plot predicted effects library(R2jags) peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) Xmat = model.matrix(~log10(AREA), data = newdata) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) fit = apply(fit, 2, function(x) rnorm(length(x), x, peakquinn.mcmc[, "sigma2"]))
Error in peakquinn.mcmc[, "sigma2"]: subscript out of bounds
newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
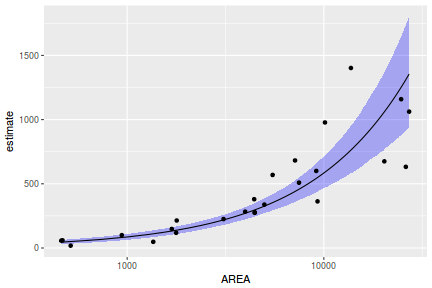
## Plot effects library(R2jags) peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix[, c("alpha", "beta")] # generate a model matrix newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) Xmat = model.matrix(~log10(AREA), data = newdata) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
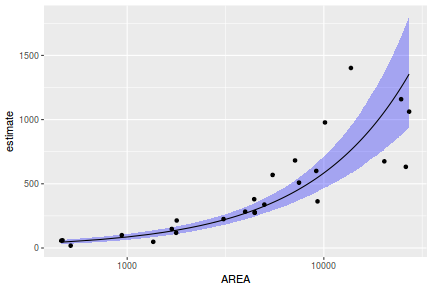 Show RSTAN code
Show RSTAN codelibrary(rstan) peakquinn.mcmc = as.matrix(peakquinn.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
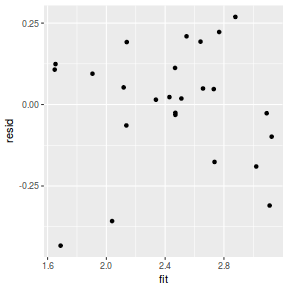
library(rstan) peakquinn.mcmc = as.matrix(peakquinn.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit ggplot() + geom_point(data = NULL, aes(y = resid, x = peakquinn$AREA)) + scale_x_log10()
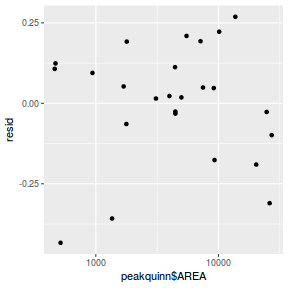
library(rstan) peakquinn.mcmc = as.matrix(peakquinn.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = data.frame(AREA = peakquinn$AREA) Xmat = model.matrix(~log10(AREA), newdata) ## get median parameter estimates coefs = apply(peakquinn.mcmc[, 1:2], 2, median) fit = as.vector(coefs %*% t(Xmat)) resid = log10(peakquinn$INDIV) - fit sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
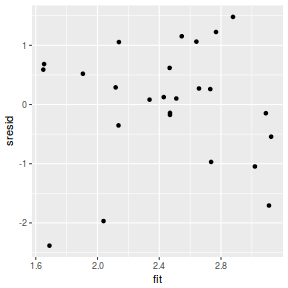
library(rstan) peakquinn.mcmc = as.matrix(peakquinn.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix Xmat = model.matrix(~log10(AREA), peakquinn) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) ## draw samples from this model yRep = sapply(1:nrow(peakquinn.mcmc), function(i) rnorm(nrow(peakquinn), fit[i, ], peakquinn.mcmc[i, "sigma"])) ggplot() + geom_density(data = NULL, aes(x = as.vector(10^yRep), fill = "Model"), alpha = 0.5) + geom_density(data = peakquinn, aes(x = INDIV, fill = "Obs"), alpha = 0.5) + scale_x_log10()
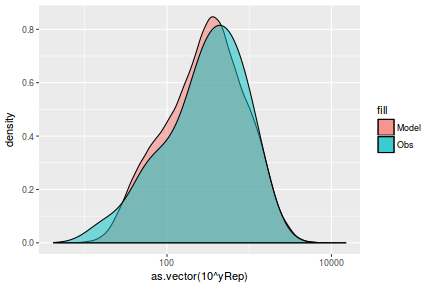
## Plot predicted effects library(rstan) peakquinn.mcmc = as.matrix(peakquinn.rstan)[, c("beta0", "beta[1]", "sigma")] # generate a model matrix newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) Xmat = model.matrix(~log10(AREA), data = newdata) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) fit = apply(fit, 2, function(x) rnorm(length(x), x, peakquinn.mcmc[, "sigma"])) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
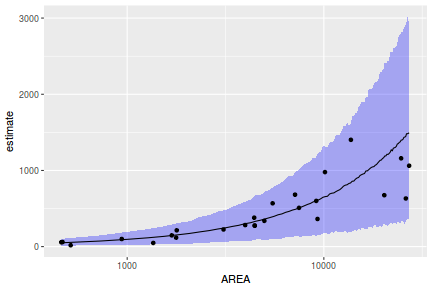
## Plot effects library(rstan) peakquinn.mcmc = as.matrix(peakquinn.rstan)[, c("beta0", "beta[1]")] # generate a model matrix newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) Xmat = model.matrix(~log10(AREA), data = newdata) ## get median parameter estimates coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
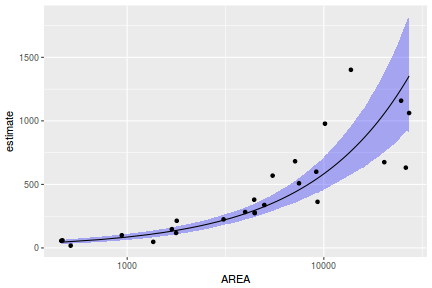 Show RSTANARM code
Show RSTANARM codelibrary(rstanarm) resid = resid(peakquinn.rstanarm) fit = fitted(peakquinn.rstanarm) ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
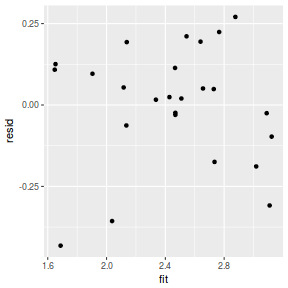
ggplot() + geom_point(data = NULL, aes(y = resid, x = peakquinn$AREA)) + scale_x_log10()
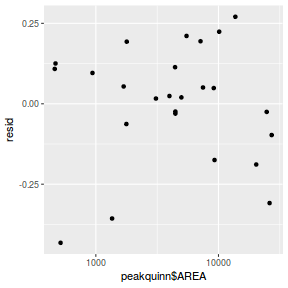
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
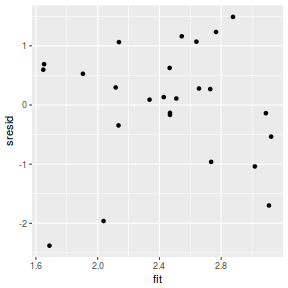
y_pred = posterior_predict(peakquinn.rstanarm) newdata = peakquinn %>% cbind(t(y_pred)) %>% gather(key = "Rep", value = "Value", -INDIV, -AREA) ggplot(newdata, aes(10^Value, x = AREA)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = peakquinn, aes(y = INDIV, x = AREA), fill = "red", color = "red", alpha = 0.5) + scale_y_log10()
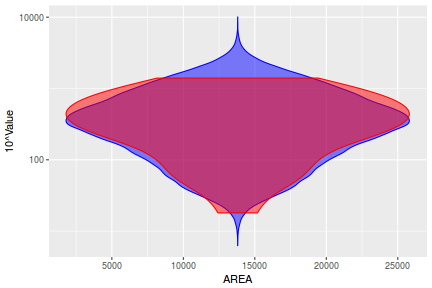
## Calculate the fitted values newdata = data.frame(AREA = seq(min(peakquinn$AREA, na.rm = TRUE), max(peakquinn$AREA, na.rm = TRUE), len = 1000)) fit = posterior_predict(peakquinn.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_continuous("Individuals") + scale_x_log10("Area") + theme_classic()
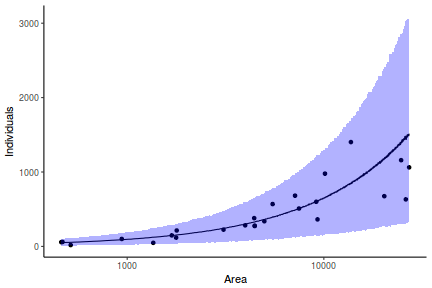
## Marginal plots pp_check(peakquinn.rstanarm, x = peakquinn$AREA, plotfun = "ribbon")
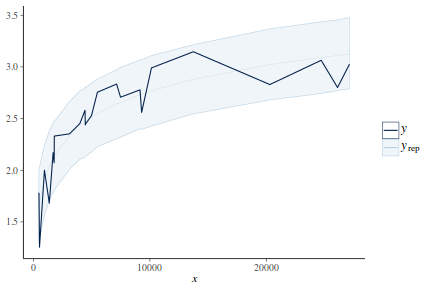
newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 100))) fit = posterior_linpred(peakquinn.rstanarm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + geom_line() + geom_point(data = peakquinn, aes(y = INDIV)) + scale_x_log10()
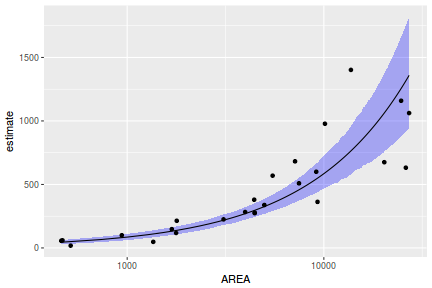 Show BRMS code
Show BRMS codelibrary(brms) resid = resid(peakquinn.brm)[, "Estimate"] fit = fitted(peakquinn.brm)[, "Estimate"] ggplot() + geom_point(data = NULL, aes(y = resid, x = fit))
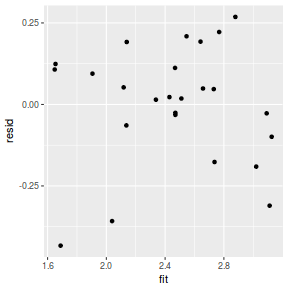
ggplot() + geom_point(data = NULL, aes(y = resid, x = peakquinn$AREA)) + scale_x_log10()
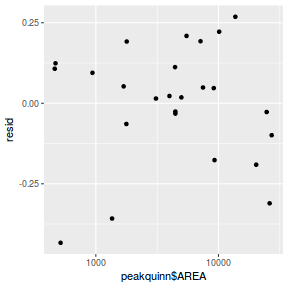
sresid = resid/sd(resid) ggplot() + geom_point(data = NULL, aes(y = sresid, x = fit))
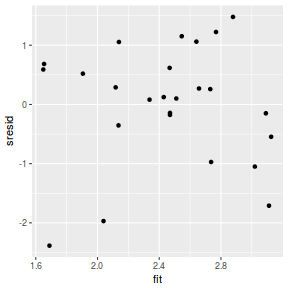
y_pred = posterior_predict(peakquinn.brm) newdata = peakquinn %>% cbind(t(10^y_pred)) %>% gather(key = "Rep", value = "Value", -INDIV, -AREA) ggplot(newdata, aes(Value, x = AREA)) + geom_violin(color = "blue", fill = "blue", alpha = 0.5) + geom_violin(data = peakquinn, aes(y = INDIV, x = AREA), fill = "red", color = "red", alpha = 0.5)
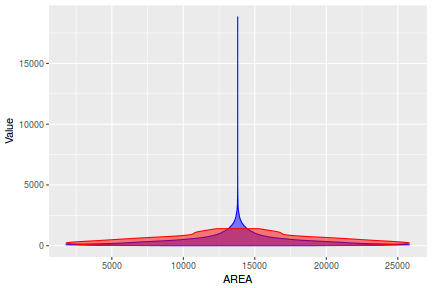
## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) fit = posterior_predict(peakquinn.brm, newdata = newdata) newdata = newdata %>% cbind(tidyMCMC(as.mcmc(10^fit), conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_log10("Individual") + scale_x_log10("AREA") + theme_classic()
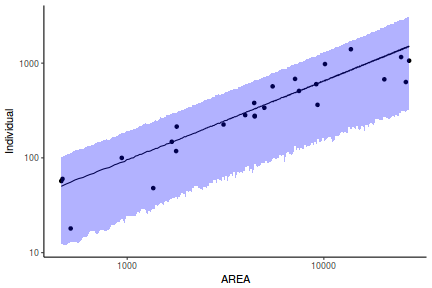
# marginal effects plots marginal_effects(peakquinn.brm)
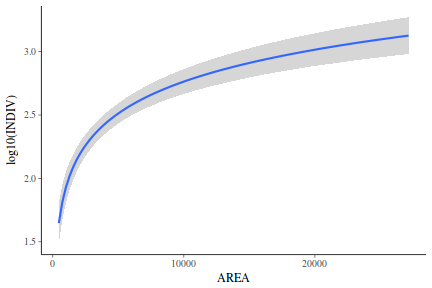
marginal_effects(peakquinn.brm, spaghetti = TRUE, nsamples = 100)
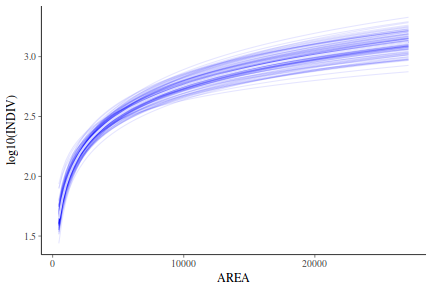
- Explore parameter estimates
Show MCMCpack code
library(MCMCpack) summary(peakquinn.mcmcpack)
Iterations = 1001:11000 Thinning interval = 1 Number of chains = 1 Sample size per chain = 10000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE (Intercept) -0.57131 0.27251 0.0027251 0.0026703 log10(AREA) 0.83362 0.07441 0.0007441 0.0007266 sigma2 0.03792 0.01237 0.0001237 0.0001336 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% (Intercept) -1.10158 -0.74580 -0.56897 -0.39754 -0.02977 log10(AREA) 0.68383 0.78651 0.83319 0.88169 0.97917 sigma2 0.02092 0.02922 0.03558 0.04388 0.06803library(broom) tidyMCMC(peakquinn.mcmcpack, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 (Intercept) -0.57130607 0.27250947 -1.09609681 -0.02482494 2 log10(AREA) 0.83362289 0.07441021 0.69012962 0.98468559 3 sigma2 0.03792093 0.01236899 0.01882708 0.06283368
mcmcpvalue(peakquinn.mcmcpack[, 2])
[1] 0
Show JAGS codelibrary(R2jags) print(peakquinn.r2jags)
Inference for Bugs model at "5", fit using jags, 3 chains, each with 166667 iterations (first 2000 discarded), n.thin = 10 n.sims = 49401 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff alpha -0.577 0.269 -1.111 -0.754 -0.576 -0.400 -0.051 1.001 49000 beta 0.835 0.074 0.692 0.787 0.835 0.884 0.980 1.001 49000 sigma 0.192 0.030 0.144 0.171 0.188 0.209 0.260 1.001 49000 deviance -12.183 2.579 -15.118 -14.064 -12.846 -11.015 -5.506 1.001 49000 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 3.3 and DIC = -8.9 DIC is an estimate of expected predictive error (lower deviance is better).# OR library(broom) tidyMCMC(as.mcmc(peakquinn.r2jags), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 alpha -0.5767199 0.26947606 -1.1116200 -0.05173172 2 beta 0.8351474 0.07352653 0.6919211 0.98028459 3 deviance -12.1825546 2.57915960 -15.3448785 -7.08681085 4 sigma 0.1915678 0.02967345 0.1381878 0.25108823
mcmcpvalue(peakquinn.r2jags$BUGSoutput$sims.matrix[, c("beta")])
[1] 0
Show RSTAN codelibrary(rstan) summary(peakquinn.rstan)
$summary mean se_mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8345211 0.0009406821 0.07702748 0.6799697 0.7852477 0.8345370 0.8840285 0.98908670 cbeta0 2.4528078 0.0004956690 0.03949651 2.3752328 2.4265938 2.4531440 2.4790586 2.53016722 sigma 0.1965092 0.0004195304 0.03106664 0.1466567 0.1745136 0.1926655 0.2135549 0.26847916 beta0 -0.5749167 0.0034557717 0.28196149 -1.1407613 -0.7548507 -0.5752530 -0.3930258 -0.01323992 lp__ 27.3242350 0.0198008852 1.32765528 23.9179494 26.7312808 27.6889601 28.2850874 28.80824526 n_eff Rhat beta[1] 6705.105 0.9998404 cbeta0 6349.418 1.0003088 sigma 5483.549 1.0000511 beta0 6657.168 0.9999017 lp__ 4495.743 0.9999604 $c_summary , , chains = chain:1 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8351555 0.07682432 0.6775663 0.7861514 0.8365360 0.8846239 0.98903431 cbeta0 2.4537252 0.03880553 2.3809506 2.4284368 2.4538544 2.4793976 2.53310501 sigma 0.1957253 0.03092306 0.1459999 0.1735727 0.1922146 0.2131895 0.26609723 beta0 -0.5763009 0.28055386 -1.1323779 -0.7552083 -0.5821777 -0.3938731 -0.01575746 lp__ 27.3305899 1.29924695 23.9320943 26.7539850 27.6608027 28.2813034 28.78446771 , , chains = chain:2 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8352273 0.07862704 0.6781426 0.7833919 0.8351356 0.8844430 0.99766912 cbeta0 2.4516565 0.04038111 2.3744419 2.4250195 2.4519134 2.4788291 2.52975216 sigma 0.1974370 0.03114833 0.1487654 0.1759307 0.1929279 0.2143715 0.26959720 beta0 -0.5786301 0.28754632 -1.1756092 -0.7569717 -0.5795402 -0.3873010 -0.01341378 lp__ 27.2996775 1.36323093 23.9833846 26.6752326 27.6914222 28.2780846 28.81726593 , , chains = chain:3 stats parameter mean sd 2.5% 25% 50% 75% 97.5% beta[1] 0.8331806 0.07561802 0.6851647 0.7866751 0.8324022 0.8830087 0.98128877 cbeta0 2.4530416 0.03927576 2.3732891 2.4273354 2.4539602 2.4791965 2.52623002 sigma 0.1963653 0.03111777 0.1460359 0.1743035 0.1928699 0.2132741 0.26946511 beta0 -0.5698192 0.27774535 -1.1144012 -0.7498764 -0.5687562 -0.3958906 -0.01360829 lp__ 27.3424375 1.31990785 23.8372128 26.7597502 27.7054566 28.3026957 28.82123035# OR library(broom) tidyMCMC(peakquinn.rstan, conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 beta[1] 0.8345211 0.07702748 0.6713353 0.97767334 2 cbeta0 2.4528078 0.03949651 2.3746189 2.52891005 3 sigma 0.1965092 0.03106664 0.1412711 0.25845271 4 beta0 -0.5749167 0.28196149 -1.1347320 -0.01195529
mcmcpvalue(as.matrix(peakquinn.rstan)[, c("beta[1]")])
[1] 0
Show RSTANARM codelibrary(rstanarm) summary(peakquinn.rstanarm)
Model Info: function: stan_glm family: gaussian [identity] formula: log10(INDIV) ~ log10(AREA) algorithm: sampling priors: see help('prior_summary') sample: 6750 (posterior sample size) num obs: 25 Estimates: mean sd 2.5% 25% 50% 75% 97.5% (Intercept) -0.6 0.3 -1.1 -0.8 -0.6 -0.4 0.0 log10(AREA) 0.8 0.1 0.7 0.8 0.8 0.9 1.0 sigma 0.2 0.0 0.1 0.2 0.2 0.2 0.3 mean_PPD 2.5 0.1 2.3 2.4 2.5 2.5 2.6 log-posterior -3.4 1.3 -6.7 -4.0 -3.1 -2.5 -1.9 Diagnostics: mcse Rhat n_eff (Intercept) 0.0 1.0 5690 log10(AREA) 0.0 1.0 5837 sigma 0.0 1.0 4379 mean_PPD 0.0 1.0 5756 log-posterior 0.0 1.0 3540 For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).# OR library(broom) tidyMCMC(peakquinn.rstanarm$stanfit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 (Intercept) -0.5836557 0.27940726 -1.1643511 -0.05480217 1.0007659 5690 2 log10(AREA) 0.8369915 0.07598716 0.6827345 0.98388027 1.0007140 5837 3 sigma 0.1962711 0.03115469 0.1408551 0.25886522 0.9995939 4379 4 mean_PPD 2.4531215 0.05594231 2.3406396 2.56302601 0.9997911 5756 5 log-posterior -3.4051806 1.27356338 -5.9644873 -1.79561380 1.0000918 3540
mcmcpvalue(as.matrix(peakquinn.rstanarm)[, c("log10(AREA)")])
[1] 0
posterior_interval(peakquinn.rstanarm, prob = 0.95)
2.5% 97.5% (Intercept) -1.1490159 -0.03698934 log10(AREA) 0.6878909 0.99053120 sigma 0.1470404 0.26706512
(full = loo(peakquinn.rstanarm))
Computed from 6750 by 25 log-likelihood matrix Estimate SE elpd_loo 4.0 4.0 p_loo 3.4 1.3 looic -8.0 8.0 Pareto k diagnostic values: Count Pct (-Inf, 0.5] (good) 24 96.0% (0.5, 0.7] (ok) 1 4.0% (0.7, 1] (bad) 0 0.0% (1, Inf) (very bad) 0 0.0% All Pareto k estimates are ok (k < 0.7) See help('pareto-k-diagnostic') for details.(reduced = loo(update(peakquinn.rstanarm, formula = . ~ 1)))
Gradient evaluation took 2.7e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.27 seconds. Adjust your expectations accordingly! Elapsed Time: 0.012857 seconds (Warm-up) 0.090834 seconds (Sampling) 0.103691 seconds (Total) Gradient evaluation took 8e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.08 seconds. Adjust your expectations accordingly! Elapsed Time: 0.011185 seconds (Warm-up) 0.089029 seconds (Sampling) 0.100214 seconds (Total) Gradient evaluation took 8e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.08 seconds. Adjust your expectations accordingly! Elapsed Time: 0.010407 seconds (Warm-up) 0.092465 seconds (Sampling) 0.102872 seconds (Total)Computed from 6750 by 25 log-likelihood matrix Estimate SE elpd_loo -19.0 3.7 p_loo 2.0 0.8 looic 38.0 7.3 All Pareto k estimates are good (k < 0.5) See help('pareto-k-diagnostic') for details.par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
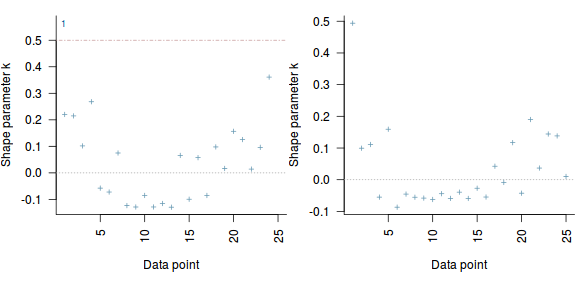
compare_models(full, reduced)
elpd_diff se -23.0 2.3Show BRMS codelibrary(brms) summary(peakquinn.brm)
Family: gaussian(identity) Formula: log10(INDIV) ~ log10(AREA) Data: peakquinn (Number of observations: 25) Samples: 3 chains, each with iter = 5000; warmup = 500; thin = 2; total post-warmup samples = 6750 ICs: LOO = Not computed; WAIC = Not computed Population-Level Effects: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat Intercept -0.58 0.28 -1.12 -0.02 6035 1 log10AREA 0.83 0.08 0.68 0.98 5996 1 Family Specific Parameters: Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat sigma 0.2 0.03 0.15 0.27 5767 1 Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat = 1).# OR library(broom) tidyMCMC(peakquinn.brm$fit, conf.int = TRUE, conf.method = "HPDinterval", rhat = TRUE, ess = TRUE)
term estimate std.error conf.low conf.high rhat ess 1 b_Intercept -0.5760033 0.27691811 -1.1462869 -0.05047086 0.9996657 6035 2 b_log10AREA 0.8348254 0.07564679 0.6799105 0.97781209 0.9996749 5996 3 sigma 0.1965642 0.03131567 0.1396273 0.25739764 0.9999035 5767
mcmcpvalue(as.matrix(peakquinn.brm)[, c("b_log10AREA")])
[1] 0
posterior_interval(as.matrix(peakquinn.brm), prob = 0.95)
2.5% 97.5% b_Intercept -1.120862 -0.02375458 b_log10AREA 0.684706 0.98353056 sigma 0.146823 0.26839084 lp__ 23.838600 28.81180829
(full = loo(peakquinn.brm))
LOOIC SE -7.83 8.23
(reduced = loo(update(peakquinn.brm, formula = . ~ 1)))
SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Gradient evaluation took 1.5e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.028246 seconds (Warm-up) 0.031009 seconds (Sampling) 0.059255 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Gradient evaluation took 1.4e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.14 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.027503 seconds (Warm-up) 0.029819 seconds (Sampling) 0.057322 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Gradient evaluation took 3e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.023562 seconds (Warm-up) 0.020834 seconds (Sampling) 0.044396 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 1). Gradient evaluation took 1.1e-05 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.028057 seconds (Warm-up) 0.030096 seconds (Sampling) 0.058153 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 2). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.027028 seconds (Warm-up) 0.028926 seconds (Sampling) 0.055954 seconds (Total) SAMPLING FOR MODEL 'gaussian(identity) brms-model' NOW (CHAIN 3). Gradient evaluation took 5e-06 seconds 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds. Adjust your expectations accordingly! Iteration: 1 / 5000 [ 0%] (Warmup) Iteration: 500 / 5000 [ 10%] (Warmup) Iteration: 1000 / 5000 [ 20%] (Warmup) Iteration: 1500 / 5000 [ 30%] (Warmup) Iteration: 2000 / 5000 [ 40%] (Warmup) Iteration: 2500 / 5000 [ 50%] (Warmup) Iteration: 2501 / 5000 [ 50%] (Sampling) Iteration: 3000 / 5000 [ 60%] (Sampling) Iteration: 3500 / 5000 [ 70%] (Sampling) Iteration: 4000 / 5000 [ 80%] (Sampling) Iteration: 4500 / 5000 [ 90%] (Sampling) Iteration: 5000 / 5000 [100%] (Sampling) Elapsed Time: 0.027537 seconds (Warm-up) 0.024572 seconds (Sampling) 0.052109 seconds (Total)LOOIC SE 37.81 7.22
par(mfrow = 1:2, mar = c(5, 3.8, 1, 0) + 0.1, las = 3) plot(full, label_points = TRUE) plot(reduced, label_points = TRUE)
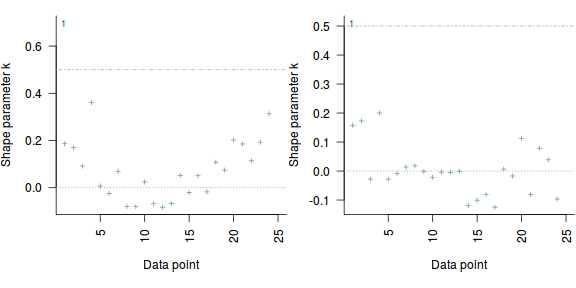
compare_models(full, reduced)
Error in discrete == discrete[1]: comparison of these types is not implemented
- Generate graphical summaries
Show MCMCpack code
library(MCMCpack) peakquinn.mcmc = peakquinn.mcmcpack ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(10^fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV, x = AREA)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
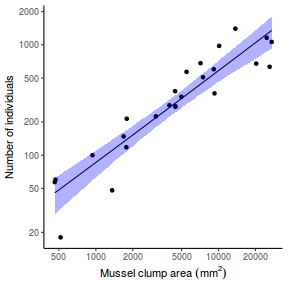
library(MCMCpack) peakquinn.mcmc = peakquinn.mcmcpack ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, 1:2] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(10^fit)) newdata = newdata %>% gather(key = Sample, value = fit, -AREA, ) newdata.sum = newdata %>% group_by(AREA) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_line(aes(y = fit, x = AREA, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = AREA), color = "blue") + geom_point(data = peakquinn, aes(y = INDIV, x = AREA), color = "red") + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
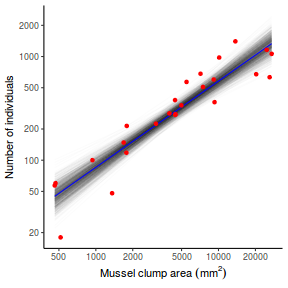 Show JAGS code
Show JAGS codepeakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(10^fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV, x = AREA)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
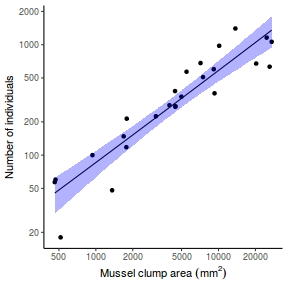
peakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("alpha", "beta")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(10^fit)) newdata = newdata %>% gather(key = Sample, value = fit, -AREA, ) newdata.sum = newdata %>% group_by(AREA) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_line(aes(y = fit, x = AREA, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = AREA), color = "blue") + geom_point(data = peakquinn, aes(y = INDIV, x = AREA), color = "red") + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
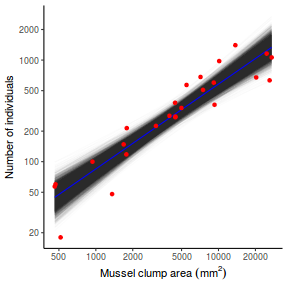 Show RSTAN code
Show RSTAN codepeakquinn.mcmc = as.matrix(peakquinn.rstan) ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(10^fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV, x = AREA)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
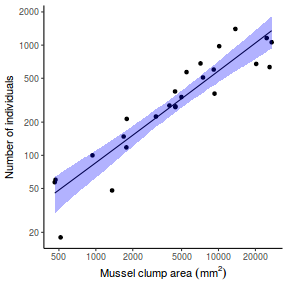
peakquinn.mcmc = as.matrix(peakquinn.rstan) ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("beta0", "beta[1]")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(10^fit)) newdata = newdata %>% gather(key = Sample, value = fit, -AREA, ) newdata.sum = newdata %>% group_by(AREA) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_line(aes(y = fit, x = AREA, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = AREA), color = "blue") + geom_point(data = peakquinn, aes(y = INDIV, x = AREA), color = "red") + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
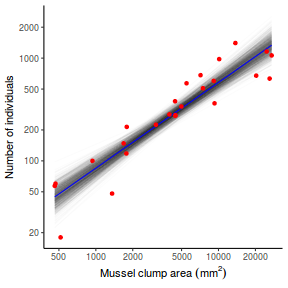 Show RSTANARM code
Show RSTANARM codepeakquinn.mcmc = as.matrix(peakquinn.rstanarm) ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(tidyMCMC(10^fit, conf.int = TRUE, conf.method = "HPDinterval")) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV, x = AREA)) + geom_line() + geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "blue", alpha = 0.3) + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
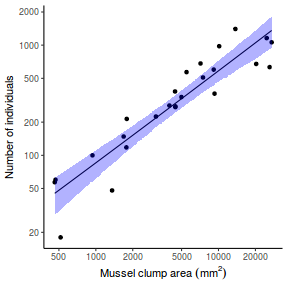
peakquinn.mcmc = as.matrix(peakquinn.rstanarm) ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(10^fit)) newdata = newdata %>% gather(key = Sample, value = fit, -AREA, ) newdata.sum = newdata %>% group_by(AREA) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_line(aes(y = fit, x = AREA, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = AREA), color = "blue") + geom_point(data = peakquinn, aes(y = INDIV, x = AREA), color = "red") + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
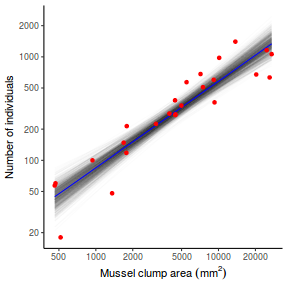 Show BRMS code
Show BRMS codenewdata = marginal_effects(peakquinn.brm)$AREA newdata = newdata %>% mutate_at(vars(estimate__, lower__, upper__), function(x) 10^x) ggplot(newdata, aes(y = estimate__, x = AREA)) + geom_point(data = peakquinn, aes(y = INDIV, x = AREA)) + geom_line() + geom_ribbon(aes(ymin = lower__, ymax = upper__), fill = "blue", alpha = 0.3) + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
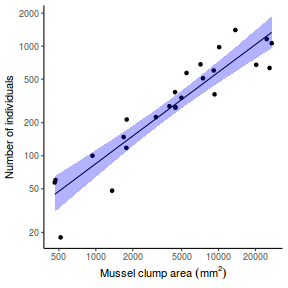
peakquinn.mcmc = as.matrix(peakquinn.brm) ## Calculate the fitted values newdata = with(peakquinn, data.frame(AREA = seq(min(AREA, na.rm = TRUE), max(AREA, na.rm = TRUE), len = 1000))) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("b_Intercept", "b_log10AREA")] fit = coefs %*% t(Xmat) newdata = newdata %>% cbind(t(10^fit)) newdata = newdata %>% gather(key = Sample, value = fit, -AREA, ) newdata.sum = newdata %>% group_by(AREA) %>% dplyr:::summarize(fit = median(fit)) ## reduce the number of lines from over 6000 to 200 newdata = newdata %>% filter(Sample < 201) ggplot(newdata, aes(y = estimate, x = AREA)) + geom_line(aes(y = fit, x = AREA, group = Sample), alpha = 0.01) + geom_line(data = newdata.sum, aes(y = fit, x = AREA), color = "blue") + geom_point(data = peakquinn, aes(y = INDIV, x = AREA), color = "red") + scale_y_log10(expression(Number ~ of ~ individuals), breaks = c(1, 2, 5) %o% 10^c(-1:3)) + scale_x_log10(expression(Mussel ~ clump ~ area ~ (mm^{ 2 })), breaks = c(1, 2, 5) %o% 10^c(0:4)) + theme_classic()
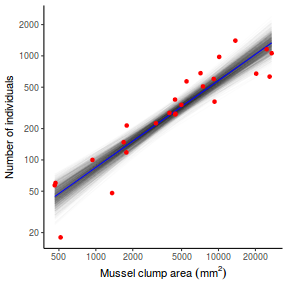
- Explore effect sizes. Lets base this on a doubling in mussel clump area from 5000$mm^2$ to 10,000$mm^2$.
Show MCMCpack code
library(MCMCpack) peakquinn.mcmc = peakquinn.mcmcpack newdata = data.frame(AREA = c(5000, 10000)) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = 10^(coefs %*% t(Xmat)) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 256.6267 40.81119 175.6593 336.0038
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/sqrt(peakquinn.mcmc[, "sigma2"]) (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1365.205 293.8033 809.7041 1956.093
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 78.45249 9.200604 60.57998 97.03649
# Probability that the effect is greater than 100% sum(ESp > 100)/length(ESp)
[1] 0.0128
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1.784525 0.09200604 1.6058 1.970365
Show JAGS codepeakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix newdata = data.frame(AREA = c(5000, 10000)) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("alpha", "beta")] fit = 10^(coefs %*% t(Xmat)) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 257.3033 40.31442 180.5504 337.299
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/peakquinn.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1373.274 287.682 821.8336 1943.753
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 78.63583 9.115099 61.54332 97.28545
# Probability that the effect is greater than 100% sum(ESp > 100)/length(ESp)
[1] 0.0147163
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1.786358 0.09115099 1.615433 1.972855
Show RSTAN codepeakquinn.mcmc = as.matrix(peakquinn.rstan) newdata = data.frame(AREA = c(5000, 10000)) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("beta0", "beta[1]")] fit = 10^(coefs %*% t(Xmat)) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 256.9233 41.95914 177.3289 340.1042
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/peakquinn.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1338.051 290.3574 744.3034 1875.826
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 78.58077 9.540803 59.25463 96.92869
# Probability that the effect is greater than 100% sum(ESp > 100)/length(ESp)
[1] 0.01911111
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1.785808 0.09540803 1.592546 1.969287
Show RSTANARM codepeakquinn.mcmc = as.matrix(peakquinn.rstanarm) newdata = data.frame(AREA = c(5000, 10000)) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = 10^(coefs %*% t(Xmat)) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 258.0592 41.27676 177.8736 337.9139
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/peakquinn.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1346.056 289.6647 821.0758 1950.451
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 78.88025 9.441726 60.33071 97.57047
# Probability that the effect is greater than 100% sum(ESp > 100)/length(ESp)
[1] 0.01940741
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1.788802 0.09441726 1.603307 1.975705
Show BRMS codepeakquinn.mcmc = as.matrix(peakquinn.brm) newdata = data.frame(AREA = c(5000, 10000)) Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("b_Intercept", "b_log10AREA")] fit = 10^(coefs %*% t(Xmat)) ## Raw effect size (RES = tidyMCMC(as.mcmc(fit[, 2] - fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 257.0839 41.93587 173.4779 335.417
## Cohen's D cohenD = (fit[, 2] - fit[, 1])/peakquinn.mcmc[, "sigma"] (cohenDES = tidyMCMC(as.mcmc(cohenD), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1338.203 285.7687 816.383 1929.084
# Percentage change ESp = 100 * (fit[, 2] - fit[, 1])/fit[, 1] (PES = tidyMCMC(as.mcmc(ESp), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 78.60938 9.368605 59.65756 96.38583
# Probability that the effect is greater than 100% sum(ESp > 100)/length(ESp)
[1] 0.01511111
## fractional change fit = fit[fit[, 2] > 0, ] (FES = tidyMCMC(as.mcmc(fit[, 2]/fit[, 1]), conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 var1 1.786094 0.09368605 1.596576 1.963858
- Finite-population standard deviations
Show MCMCpack code
library(MCMCpack) peakquinn.mcmc = peakquinn.mcmcpack newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = 10^(coefs %*% t(Xmat)) resid = sweep(fit, 2, peakquinn$INDIV, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$AREA[2] - newdata$AREA[1])) * sd(peakquinn$AREA) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 660.8782 75.05975 512.5846 809.6377 2 sd.resid 251.2939 36.89695 211.2944 324.1390
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 72.95323 3.908862 64.07417 78.92681 2 sd.resid 27.04677 3.908862 21.07319 35.92583
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
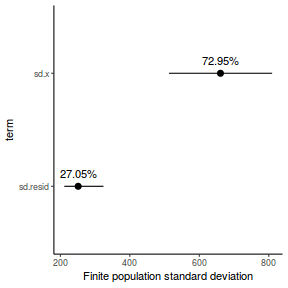 Show JAGS code
Show JAGS codepeakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("alpha", "beta")] fit = 10^(coefs %*% t(Xmat)) resid = sweep(fit, 2, peakquinn$INDIV, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$AREA[2] - newdata$AREA[1])) * sd(peakquinn$AREA) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 660.1122 74.43848 515.7628 806.9890 2 sd.resid 251.6663 36.80898 211.2570 324.5143
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 72.86154 3.9199 64.30474 79.16061 2 sd.resid 27.13846 3.9199 20.83939 35.69526
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
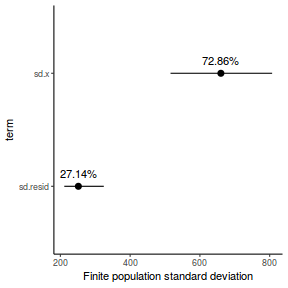 Show RSTAN code
Show RSTAN codepeakquinn.mcmc = as.matrix(peakquinn.rstan) newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("beta0", "beta[1]")] fit = 10^(coefs %*% t(Xmat)) resid = sweep(fit, 2, peakquinn$INDIV, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$AREA[2] - newdata$AREA[1])) * sd(peakquinn$AREA) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 659.7561 76.17899 508.2497 807.5814 2 sd.resid 252.1489 38.36843 210.6826 327.9973
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 72.86224 4.081213 64.21619 79.58738 2 sd.resid 27.13776 4.081213 20.41262 35.78381
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
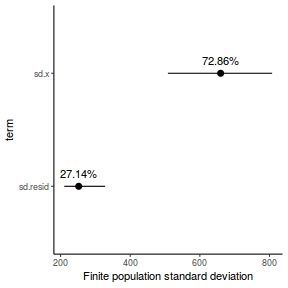 Show RSTANARM code
Show RSTANARM codepeakquinn.mcmc = as.matrix(peakquinn.rstanarm) newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = 10^(coefs %*% t(Xmat)) resid = sweep(fit, 2, peakquinn$INDIV, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$AREA[2] - newdata$AREA[1])) * sd(peakquinn$AREA) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 658.8303 77.98878 512.2534 820.9864 2 sd.resid 252.8086 38.02596 211.3581 330.0817
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 72.83891 4.106887 63.33252 78.94102 2 sd.resid 27.16109 4.106887 21.05898 36.66748
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
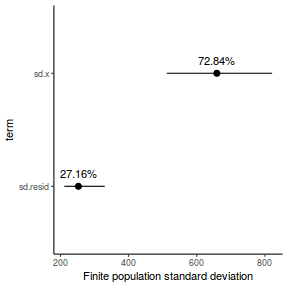 Show BRMS code
Show BRMS codepeakquinn.mcmc = as.matrix(peakquinn.brm) newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("b_Intercept", "b_log10AREA")] fit = 10^(coefs %*% t(Xmat)) resid = sweep(fit, 2, peakquinn$INDIV, "-") sd.resid = apply(resid, 1, sd) sd.x = abs((fit[, 2] - fit[, 1])/(newdata$AREA[2] - newdata$AREA[1])) * sd(peakquinn$AREA) sd.all = cbind(sd.x, sd.resid) (fpsd = tidyMCMC(sd.all, conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 659.7398 76.91358 508.5955 810.7227 2 sd.resid 252.1473 38.46217 210.1392 325.3136
# OR expressed as a percentage (fpsd.p = tidyMCMC(100 * sd.all/rowSums(sd.all), estimate.method = "median", conf.int = TRUE, conf.method = "HPDinterval"))
term estimate std.error conf.low conf.high 1 sd.x 72.82011 4.014486 64.0221 79.2249 2 sd.resid 27.17989 4.014486 20.7751 35.9779
ggplot(fpsd, aes(y = estimate, x = term)) + geom_pointrange(aes(ymin = conf.low, ymax = conf.high)) + geom_text(aes(label = sprintf("%.2f%%", fpsd.p$estimate), vjust = -1)) + scale_y_continuous("Finite population standard deviation") + scale_x_discrete() + coord_flip() + theme_classic()
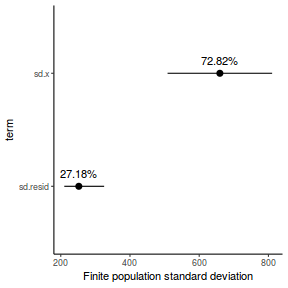
- $R^2$
Show MCMCpack code
library(MCMCpack) peakquinn.mcmc = peakquinn.mcmcpack newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = (coefs %*% t(Xmat)) x = log10(peakquinn$INDIV) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.8498102 0.02907766 0.795766 0.8760876
# for comparison summary(lm(log10(INDIV) ~ log10(AREA), data = peakquinn))
Call: lm(formula = log10(INDIV) ~ log10(AREA), data = peakquinn) Residuals: Min 1Q Median 3Q Max -0.43355 -0.06464 0.02219 0.11178 0.26818 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.57601 0.25904 -2.224 0.0363 * log10(AREA) 0.83492 0.07066 11.816 3.01e-11 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.1856 on 23 degrees of freedom Multiple R-squared: 0.8586, Adjusted R-squared: 0.8524 F-statistic: 139.6 on 1 and 23 DF, p-value: 3.007e-11Show JAGS codepeakquinn.mcmc = peakquinn.r2jags$BUGSoutput$sims.matrix newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("alpha", "beta")] fit = (coefs %*% t(Xmat)) x = log10(peakquinn$INDIV) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.8505598 0.02721339 0.7984761 0.8760876
Show RSTAN codepeakquinn.mcmc = as.matrix(peakquinn.rstan) newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("beta0", "beta[1]")] fit = (coefs %*% t(Xmat)) x = log10(peakquinn$INDIV) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.8495326 0.02996109 0.7939627 0.8760876
Show RSTANARM codepeakquinn.mcmc = as.matrix(peakquinn.rstanarm) newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("(Intercept)", "log10(AREA)")] fit = (coefs %*% t(Xmat)) x = log10(peakquinn$INDIV) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.8506467 0.02769766 0.7993714 0.8760876
Show BRMS codepeakquinn.mcmc = as.matrix(peakquinn.brm) newdata = peakquinn Xmat = model.matrix(~log10(AREA), newdata) coefs = peakquinn.mcmc[, c("b_Intercept", "b_log10AREA")] fit = (coefs %*% t(Xmat)) x = log10(peakquinn$INDIV) resid = sweep(fit, 2, x, "-") var_f = apply(fit, 1, var) var_e = apply(resid, 1, var) R2 = var_f/(var_f + var_e) tidyMCMC(as.mcmc(R2), conf.int = TRUE, conf.method = "HPDinterval")
term estimate std.error conf.low conf.high 1 var1 0.8499476 0.02852317 0.794581 0.8760876
All diagnostics appear reasonable.
