Workshop 15.1 - Non-metric Multidimensional Scaling (NMDS)
14 Jan 2013
Basic statistics references
- Legendre and Legendre
- Quinn & Keough (2002) - Chpt 17
Non-metric Multidimensional Scaling (NMDS)
The following example is designed to help you appreciate the link between distance measures and ordination space (MDS). The data set consists of distances (km) between major Australia cities (as the crow flies), and is in the form of a triangular matrix.
Download austcities data set| Format of austcites.csv data file | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||
 |
> austcities <- read.csv("../downloads/data/austcities.csv") > austcities
Canberra Sydney Melbourne Adelaide Perth Broome Alice Darwin Cairns Townsville Brisbane
Canberra 0 NA NA NA NA NA NA NA NA NA NA
Sydney 246 0 NA NA NA NA NA NA NA NA NA
Melbourne 467 713 0 NA NA NA NA NA NA NA NA
Adelaide 958 1160 653 0 NA NA NA NA NA NA NA
Perth 3090 3290 2720 2130 0 NA NA NA NA NA NA
Broome 3280 3380 3120 2490 1680 0 NA NA NA NA NA
Alice 1950 2030 1890 1330 1990 1370 0 NA NA NA NA
Darwin 3130 3150 3150 2620 2650 1110 1290 0 NA NA NA
Cairns 2060 1960 2320 2120 3440 2500 1450 1680 0 NA NA
Townsville 1790 1680 2070 1920 3390 2590 1420 1860 281 0 NA
Brisbane 941 731 1370 1600 3610 3320 1960 2850 1390 1110 0
Hobart 860 1060 597 1160 3010 3640 2460 3730 2890 2630 1790
Hobart
Canberra NA
Sydney NA
Melbourne NA
Adelaide NA
Perth NA
Broome NA
Alice NA
Darwin NA
Cairns NA
Townsville NA
Brisbane NA
Hobart 0
Note the format of the file, it is a triangular distance matrix.
- While the file is a distance matrix, at this stage R is unaware of it, we must manually make it aware (a round about way of saying that we must type a command to force R to treat the data set as a distance matrix.
Convert the data frame into a distance matrix (HINT).
Show code
> austcities <- as.dist(austcities) > austcitiesCanberra Sydney Melbourne Adelaide Perth Broome Alice Darwin Cairns Townsville Brisbane Sydney 246 Melbourne 467 713 Adelaide 958 1160 653 Perth 3090 3290 2720 2130 Broome 3280 3380 3120 2490 1680 Alice 1950 2030 1890 1330 1990 1370 Darwin 3130 3150 3150 2620 2650 1110 1290 Cairns 2060 1960 2320 2120 3440 2500 1450 1680 Townsville 1790 1680 2070 1920 3390 2590 1420 1860 281 Brisbane 941 731 1370 1600 3610 3320 1960 2850 1390 1110 Hobart 860 1060 597 1160 3010 3640 2460 3730 2890 2630 1790
-
Perform an MDS with 2 dimensions on the city distances matrix (HINT).
Show code
> library(vegan) > austcities.mds <- metaMDS(austcities, k = 2)
Run 0 stress 0 Run 1 stress 0.169 Run 2 stress 0.13 Run 3 stress 0 ... procrustes: rmse 0.003944 max resid 0.006698 *** Solution reached
- What was the final stress value (as a percentage)?
Show code
> austcities.mds$stress
[1] 0
- What does this stress value suggest about the success of the MDS?
- Generate a Shepard diagram.
The Shepard diagram (plot) represents the relationship between the original distances (y-axis) and the new MDS ordination distances (x-axis).
Does this and the stress value indicate that the patterns present in the original distance matrix (crow flies distances between cities)
are adequately reproduced from the 2 new dimensions?
Show code
> stressplot(austcities.mds)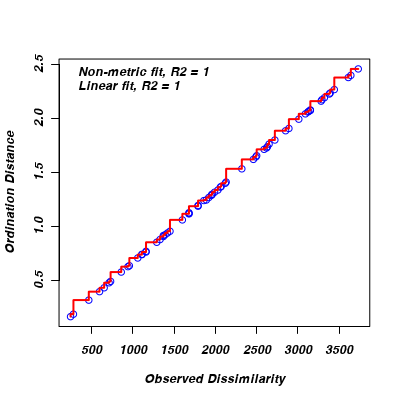
- What was the final stress value (as a percentage)?
-
Generate an ordination plot.
The final ordination plot summarizes the relationship between the cities.
Does this ordination plot approximate the true geographical arrangement of the cities?
Show codeRecall that the orientation of points in a MDS ordination plot is arbitrary. Unlike PCA and CA, the points are not orientated towards axes explaining most variance. Instead the two new dimensions simply provide the space or scope in which the points are arranged. What if we rotated the points 140 degrees. Does this make the patterns easier to relate back to reality?
> ordiplot(austcities.mds, display = "sites", type = "n") > text(austcities.mds, lab = rownames(austcities.mds$points))
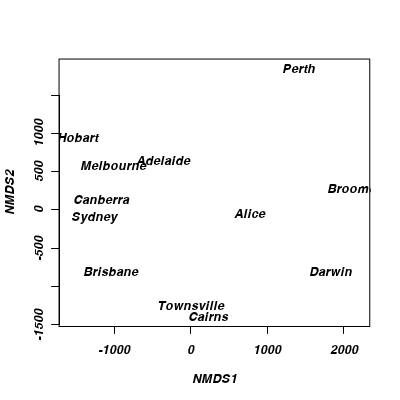 Show code
Show code> library(shape) > austcities.rot <- rotatexy(austcities.mds$points, angle = 140) > plot(austcities.rot, type = "n") > text(austcities.rot, lab = rownames(austcities.mds$points))
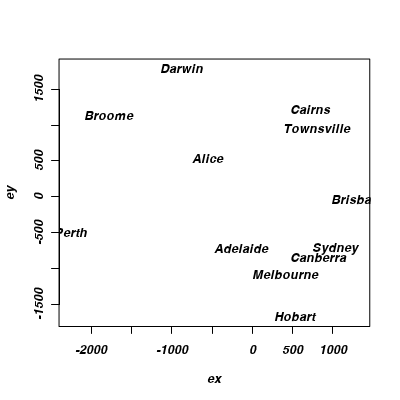
- In this case, what might the two new MDS dimensions (variables) represent?
(hint think of the ordination plot as a map)
We are now ready to perform the MDS for the purpose of examining the ordination plot.
Non-metric Multidimensional Scaling (NMDS)
Mac Nally (1989) studied geographic variation in forest bird communities. His data set consists of the maximum abundance for 102 bird species from 37 sites that where further classified into five different forest types (Gippsland manna gum, montane forest, woodland, box-ironbark and river redgum and mixed forest). He was primarily interested in determining whether the bird assemblages differed between forest types.
Download the macnally data set| Format of macnally_full.csv data file | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
> macnally <- read.csv("../downloads/data/macnally_full.csv") > macnally
HABITAT GST EYR GF BTH GWH WTTR WEHE WNHE SFW WBSW CR LK RWB AUR
Reedy Lake Mixed 3.4 0.0 0.0 0.0 0.0 0.0 0.0 11.9 0.4 0.0 1.1 3.8 9.7 0.0
Pearcedale Gipps.Manna 3.4 9.2 0.0 0.0 0.0 0.0 0.0 11.5 8.3 12.6 0.0 0.5 11.6 0.0
Warneet Gipps.Manna 8.4 3.8 0.7 2.8 0.0 0.0 10.7 12.3 4.9 10.7 0.0 1.9 16.6 2.3
Cranbourne Gipps.Manna 3.0 5.0 0.0 5.0 2.0 0.0 3.0 10.0 6.9 12.0 0.0 2.0 11.0 1.5
Lysterfield Mixed 5.6 5.6 12.9 12.2 9.5 2.1 7.9 28.6 9.2 5.0 19.1 3.6 5.7 8.8
Red Hill Mixed 8.1 4.1 10.9 24.5 5.6 6.7 9.4 6.7 0.0 8.9 12.1 6.7 2.7 0.0
Devilbend Mixed 8.3 7.1 6.9 29.1 4.2 2.0 7.1 27.4 13.1 2.8 0.0 2.8 2.4 2.8
Olinda Mixed 4.6 5.3 11.1 28.2 3.9 6.5 2.6 10.9 3.1 8.6 9.3 3.8 0.6 1.3
Fern Tree Gum Montane Forest 3.2 5.2 8.3 18.2 3.8 4.2 2.8 9.0 3.8 5.6 14.1 3.2 0.0 0.0
Sherwin Foothills Woodland 4.6 1.2 4.6 6.5 2.3 5.2 0.6 3.6 3.8 3.0 7.5 2.4 0.6 0.0
Heathcote Ju Montane Forest 3.7 2.5 6.3 24.9 2.8 7.4 1.3 4.7 5.5 9.5 5.7 2.9 0.0 1.8
Warburton Montane Forest 3.8 6.5 11.1 36.1 6.2 8.5 2.3 25.4 8.2 5.9 10.5 3.1 9.8 1.6
Millgrove Mixed 5.4 6.5 11.9 19.6 3.3 8.6 2.5 11.9 4.3 5.4 10.8 6.5 2.7 2.0
Ben Cairn Mixed 3.1 9.3 11.1 25.9 9.3 8.3 2.8 2.8 2.8 8.3 18.5 3.1 0.0 3.1
Panton Gap Montane Forest 3.8 3.8 10.3 34.6 7.9 4.8 2.9 3.7 4.8 7.2 5.9 3.1 0.6 3.8
OShannassy Mixed 9.6 4.0 5.4 34.9 7.0 5.1 2.6 6.4 3.9 11.3 11.6 2.3 0.0 2.3
Ghin Ghin Mixed 3.4 2.7 9.1 16.1 1.3 3.2 4.7 0.0 22.0 5.8 7.4 4.5 0.0 0.0
Minto Mixed 5.6 3.3 13.3 28.0 7.0 8.3 7.0 38.9 10.5 7.0 14.0 5.2 1.7 5.2
Hawke Mixed 1.7 2.6 5.5 16.0 4.3 6.7 3.5 5.9 6.7 10.0 3.7 2.1 0.5 1.5
St Andrews Foothills Woodland 4.7 3.6 6.0 25.2 3.7 7.5 4.7 10.0 0.0 0.0 4.0 5.1 2.8 3.7
Nepean Foothills Woodland 14.0 5.6 5.5 20.0 3.0 6.6 7.0 3.3 7.0 10.0 4.7 3.3 2.1 3.7
Cape Schanck Mixed 6.0 4.9 4.9 16.2 3.4 2.6 2.8 9.4 6.6 7.8 5.1 5.2 21.3 0.0
Balnarring Mixed 4.1 4.9 10.7 21.2 3.9 0.0 5.1 2.9 12.1 6.1 0.0 2.7 0.0 0.0
Bittern Gipps.Manna 6.5 9.7 7.8 14.4 5.2 0.0 11.5 12.5 20.7 4.9 0.0 0.0 16.1 5.2
Bailieston Box-Ironbark 6.5 2.5 5.1 5.6 4.3 5.7 6.2 6.2 1.2 0.0 0.0 1.6 5.0 4.1
Donna Buang Mixed 1.5 0.0 2.2 9.6 6.7 3.0 8.1 0.0 0.0 7.3 8.1 1.5 2.2 0.7
Upper Yarra Mixed 4.7 3.1 7.0 17.1 8.3 12.8 1.3 6.4 2.3 5.4 5.4 2.4 0.6 2.3
Gembrook Mixed 7.5 7.5 12.7 16.4 4.7 6.4 1.6 8.9 9.3 6.4 4.8 3.6 14.5 4.7
Arcadia River Red Gum 3.1 0.0 1.2 0.0 1.2 0.0 0.0 1.8 0.7 0.0 0.0 1.8 0.0 2.5
Undera River Red Gum 2.7 0.0 2.2 0.0 1.3 6.5 0.0 0.0 6.5 0.0 0.0 0.0 0.0 2.2
Coomboona River Red Gum 4.4 0.0 2.1 0.0 0.0 3.3 0.0 0.0 0.8 0.0 0.0 2.8 0.0 2.2
Toolamba River Red Gum 3.0 0.0 0.5 0.0 0.8 0.0 0.0 0.0 1.6 0.0 0.0 2.0 0.0 2.5
Rushworth Box-Ironbark 2.1 1.1 3.2 1.8 0.5 4.8 0.9 5.3 4.8 0.0 1.1 1.1 26.3 1.6
Sayers Box-Ironbark 2.6 0.0 1.1 7.5 1.6 5.2 3.6 6.9 6.7 0.0 2.7 1.6 8.0 1.6
Waranga Mixed 3.0 1.6 1.5 3.0 0.0 3.0 0.0 14.5 6.7 0.0 0.7 4.0 23.0 1.6
Costerfield Box-Ironbark 7.1 2.2 4.5 9.0 2.7 6.0 2.5 7.7 9.5 0.0 7.7 2.2 8.9 1.9
Tallarook Foothills Woodland 4.3 2.9 8.7 14.4 2.9 5.8 2.8 11.1 2.9 0.0 3.8 2.9 2.9 1.9
STTH LR WPHE YTH ER PCU ESP SCR RBFT BFCS WAG WWCH NHHE VS CST BTR AMAG SCC
Reedy Lake 0.0 4.8 27.3 0.0 5.1 0.0 0.0 0.0 0.0 0.6 1.9 0.0 0.0 0.0 1.7 12.5 8.6 12.5
Pearcedale 0.0 3.7 27.6 0.0 2.7 0.0 3.7 0.0 1.1 1.1 3.4 0.0 6.9 0.0 0.9 0.0 0.0 0.0
Warneet 2.8 5.5 27.5 0.0 5.3 0.0 0.0 0.0 0.0 1.5 2.1 0.0 3.0 0.0 1.5 0.0 0.0 0.0
Cranbourne 0.0 11.0 20.0 0.0 2.1 0.0 2.0 0.0 5.0 1.4 3.4 0.0 32.0 0.0 1.4 0.0 0.0 0.0
Lysterfield 7.0 1.6 0.0 0.0 1.4 0.0 3.5 0.7 0.0 2.7 0.0 0.0 6.4 0.0 0.0 0.0 0.0 0.0
Red Hill 16.8 3.4 0.0 0.0 2.2 0.0 3.4 0.0 0.7 2.0 0.0 0.0 2.2 5.4 0.0 0.0 0.0 0.0
Devilbend 13.9 0.0 16.7 0.0 0.0 0.0 5.5 0.0 0.0 3.6 0.0 0.0 5.6 5.6 4.6 0.0 0.0 0.0
Olinda 10.2 0.0 0.0 0.0 1.2 0.0 5.1 0.0 0.7 0.0 0.0 0.0 0.0 1.9 0.0 0.0 0.0 0.0
Fern Tree Gum 12.2 0.6 0.0 0.0 1.3 2.8 7.1 0.0 1.9 0.6 0.0 0.0 0.0 4.2 0.0 0.0 0.0 0.0
Sherwin 11.3 5.8 0.0 9.6 2.3 2.9 0.6 3.0 0.0 1.2 0.0 9.8 0.0 5.1 0.0 0.0 0.0 0.0
Heathcote Ju 12.0 0.0 0.0 0.0 0.0 2.8 0.9 2.6 0.0 0.0 0.0 11.7 0.0 0.0 0.0 0.0 0.0 0.0
Warburton 7.6 15.0 0.0 0.0 0.0 1.8 7.6 0.0 0.9 1.5 0.0 0.0 0.0 3.9 2.5 0.0 0.0 0.0
Millgrove 8.6 0.0 0.0 0.0 6.5 2.5 5.4 2.0 5.4 2.2 0.0 0.0 0.0 5.4 3.2 0.0 0.0 0.0
Ben Cairn 12.0 3.3 0.0 0.0 0.0 2.5 7.4 0.0 0.0 0.0 0.0 0.0 2.1 0.0 0.0 0.0 0.0 0.0
Panton Gap 17.3 2.4 0.0 0.0 0.0 3.1 9.2 0.0 3.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
OShannassy 7.8 0.0 0.0 0.0 0.0 1.5 3.1 0.0 9.6 0.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Ghin Ghin 8.1 2.7 8.4 8.4 3.4 0.0 0.0 0.0 44.7 0.4 1.3 0.0 0.4 0.6 0.6 0.0 8.4 47.6
Minto 25.2 0.0 15.4 0.0 0.0 0.0 3.3 0.0 10.5 0.0 0.0 0.0 0.0 0.0 3.5 0.0 6.7 80.5
Hawke 9.0 4.8 0.0 0.0 0.0 2.1 3.7 0.0 0.0 0.7 0.0 3.2 0.0 0.0 1.5 0.0 0.0 0.0
St Andrews 15.8 3.4 0.0 9.0 0.0 3.7 5.6 4.0 0.9 0.0 0.0 10.0 0.0 0.0 2.7 0.0 0.0 0.0
Nepean 12.0 2.2 0.0 0.0 3.7 0.0 4.0 2.0 0.0 1.1 0.0 0.0 1.1 4.5 0.0 0.0 0.0 0.0
Cape Schanck 0.0 4.3 0.0 0.0 6.4 0.0 4.6 0.0 3.4 0.0 0.0 0.0 33.3 0.0 0.0 0.0 0.0 0.0
Balnarring 4.9 16.5 0.0 0.0 9.1 0.0 3.9 0.0 2.7 1.0 0.0 0.0 4.9 10.1 0.0 0.0 0.0 0.0
Bittern 0.0 0.0 27.7 0.0 2.3 0.0 0.0 0.0 2.3 2.3 6.3 0.0 2.6 0.0 1.3 0.0 0.0 0.0
Bailieston 9.8 0.0 0.0 8.7 0.0 0.0 0.0 6.2 0.0 1.6 0.0 10.0 0.0 2.5 0.0 0.0 0.0 0.0
Donna Buang 5.2 0.0 0.0 0.0 0.0 1.5 7.4 0.0 0.0 1.5 0.0 0.0 0.0 0.0 1.5 0.0 0.0 0.0
Upper Yarra 6.4 0.0 0.0 0.0 0.0 1.3 2.3 0.0 6.4 0.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Gembrook 24.3 2.4 0.0 0.0 3.6 0.0 26.6 4.7 2.8 0.0 0.0 0.0 4.8 9.7 0.0 0.0 0.0 0.0
Arcadia 0.0 2.7 27.6 0.0 4.3 3.7 0.0 0.0 0.6 2.1 4.9 8.0 0.0 0.0 1.8 6.7 3.1 24.0
Undera 7.5 3.1 13.5 11.5 2.0 0.0 0.0 0.0 0.0 1.9 2.5 6.5 0.0 3.8 0.0 4.0 3.2 16.0
Coomboona 3.1 1.7 13.9 5.6 4.6 1.1 0.0 0.0 0.0 6.9 3.3 5.6 0.0 3.3 1.0 4.2 5.4 30.4
Toolamba 0.0 2.5 16.0 0.0 5.0 0.0 0.0 0.0 0.8 3.0 3.5 5.0 0.0 0.0 0.8 7.0 3.7 29.9
Rushworth 3.2 0.0 0.0 10.7 3.2 0.0 0.0 1.1 2.7 1.1 0.0 9.6 0.0 2.7 0.0 0.0 0.0 0.0
Sayers 7.5 2.7 0.0 20.2 1.1 0.0 0.0 2.6 0.0 0.5 0.0 5.6 0.0 0.0 0.0 0.0 0.0 0.0
Waranga 0.0 8.9 25.3 2.2 3.4 0.0 0.0 0.0 10.9 1.6 2.4 8.9 0.0 0.0 0.7 5.5 2.7 0.0
Costerfield 9.3 1.1 0.0 15.8 1.1 0.0 0.0 5.5 0.0 1.3 0.0 5.7 0.0 3.3 1.1 5.5 0.0 0.0
Tallarook 4.6 10.3 0.0 2.9 0.0 0.0 5.8 5.6 0.0 1.5 0.0 2.8 0.0 3.8 3.4 0.0 0.0 0.0
RWH WSW STP YFHE WHIP GAL FHE BRTH SPP SIL GCU MUSK MGLK BHHE RFC YTBC LYRE CHE
Reedy Lake 0.6 0.0 4.8 0.0 0.0 4.8 26.2 0.0 0.0 0.0 0.0 13.1 1.7 1.1 0.0 0.0 0.0 0.0
Pearcedale 2.3 5.7 0.0 1.1 0.0 0.0 0.0 0.0 1.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Warneet 1.4 24.3 3.1 11.7 0.0 0.0 0.0 0.0 4.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Cranbourne 0.0 10.0 4.0 0.0 0.0 2.8 0.0 0.0 0.8 0.0 0.0 0.0 1.4 0.0 0.0 0.0 0.0 0.0
Lysterfield 7.0 0.0 0.0 6.1 0.0 0.0 0.0 0.0 5.4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Red Hill 6.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 3.4 2.7 1.4 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Devilbend 7.3 3.6 2.4 0.0 0.0 0.0 0.0 0.0 0.0 1.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Olinda 9.1 0.0 0.0 0.0 2.0 0.0 0.0 0.0 2.0 0.0 2.6 0.0 0.0 0.0 0.0 1.9 0.0 0.0
Fern Tree Gum 4.5 0.0 0.0 0.0 3.2 0.0 0.0 0.0 2.6 4.9 1.3 0.0 0.0 0.0 0.0 2.6 0.6 0.6
Sherwin 6.3 0.0 3.5 2.3 0.0 0.0 0.0 6.0 4.2 1.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Heathcote Ju 5.9 0.0 4.4 4.7 0.0 0.0 0.0 0.0 3.7 2.5 1.5 0.0 0.0 0.0 0.0 1.8 0.0 0.0
Warburton 0.0 0.0 2.7 6.2 3.3 0.0 0.0 0.0 6.2 4.6 5.7 0.0 0.0 7.4 0.0 3.9 1.4 0.0
Millgrove 8.8 0.0 2.2 5.4 2.6 0.0 0.0 0.0 5.3 3.2 1.1 0.0 0.0 0.9 0.0 1.9 0.0 2.2
Ben Cairn 0.0 0.0 0.0 0.9 3.7 0.0 0.0 0.0 3.7 12.0 2.1 0.0 0.0 0.0 0.0 3.7 0.0 5.6
Panton Gap 0.0 0.0 1.2 4.9 3.8 0.0 0.0 0.0 1.9 2.4 2.9 0.0 0.0 7.7 0.0 0.0 2.4 1.8
OShannassy 3.9 0.0 3.1 8.5 2.9 0.0 0.0 0.0 2.2 3.7 0.0 0.0 0.0 0.0 0.0 1.5 1.6 8.1
Ghin Ghin 6.1 4.7 1.2 6.7 0.0 0.0 0.0 0.0 4.5 6.7 0.0 0.0 2.7 0.0 1.3 0.0 0.0 0.0
Minto 5.0 0.0 5.0 26.7 0.0 0.0 0.0 0.0 5.0 17.5 0.0 0.0 0.0 0.0 2.8 0.0 0.0 0.0
Hawke 4.2 0.0 0.0 3.2 0.0 0.0 0.0 5.2 3.7 0.0 0.0 0.0 0.0 0.5 0.0 0.0 1.7 0.0
St Andrews 8.4 0.0 5.1 5.0 0.0 0.0 0.0 10.0 5.1 0.9 3.4 0.0 0.0 1.0 0.0 0.0 0.0 0.0
Nepean 3.3 0.0 0.0 1.0 0.0 0.0 0.0 0.0 4.7 1.1 0.0 0.0 0.0 5.0 0.0 0.0 0.0 5.6
Cape Schanck 2.6 0.0 0.0 3.4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 5.2
Balnarring 4.9 0.0 0.0 1.9 0.0 0.0 0.0 0.0 0.0 10.3 0.0 0.0 0.0 3.9 0.0 0.0 0.0 0.0
Bittern 0.0 12.5 2.3 19.5 0.0 0.0 0.0 0.0 3.5 8.0 0.0 0.0 0.0 2.3 0.0 0.0 0.0 0.0
Bailieston 7.3 0.0 0.0 1.1 0.0 0.0 1.2 0.0 2.8 0.8 0.0 0.0 0.0 14.1 0.0 0.0 0.0 0.0
Donna Buang 0.0 0.0 2.2 0.0 3.7 0.0 0.0 0.0 3.7 4.4 4.4 0.0 0.0 0.0 0.0 3.6 3.0 1.5
Upper Yarra 7.0 0.0 6.4 3.9 0.9 0.0 0.0 0.0 3.9 2.3 0.0 0.0 0.0 0.6 0.0 0.8 0.9 0.9
Gembrook 10.9 0.0 0.0 20.2 0.0 0.0 0.0 0.0 4.5 1.8 1.8 0.0 0.0 5.6 0.0 5.5 0.0 11.2
Arcadia 0.0 2.7 8.2 0.0 0.0 4.1 0.0 0.0 0.0 9.8 0.0 0.0 3.7 0.0 4.3 0.0 0.0 0.0
Undera 1.5 1.0 8.7 0.0 0.0 8.6 0.0 0.0 0.0 0.0 0.0 0.0 1.6 0.0 1.5 0.0 0.0 0.0
Coomboona 1.1 0.0 8.1 0.0 0.0 5.4 0.0 0.0 0.0 0.0 0.0 0.0 2.3 0.0 2.6 0.0 0.0 0.0
Toolamba 0.0 6.0 4.5 0.0 0.0 7.8 0.0 0.0 0.0 0.0 0.0 0.0 1.6 0.0 2.0 0.0 0.0 0.0
Rushworth 4.3 0.0 1.1 14.4 0.0 0.0 9.6 11.7 3.2 2.7 1.1 16.0 0.0 9.9 0.0 0.0 0.0 0.0
Sayers 3.7 0.0 0.0 8.0 0.0 0.0 3.1 9.1 5.7 3.7 1.6 3.1 0.0 7.8 0.0 0.0 0.0 0.0
Waranga 1.4 3.4 2.7 16.3 0.0 5.9 14.8 0.0 2.2 0.0 0.0 20.0 0.0 8.1 2.7 0.0 0.0 0.0
Costerfield 6.2 0.0 6.6 0.6 0.0 0.0 15.9 13.9 6.3 3.9 1.6 3.8 0.0 10.8 0.0 0.0 0.0 0.0
Tallarook 9.5 0.0 1.9 5.8 0.0 0.0 0.0 30.6 8.3 0.0 0.9 0.0 0.0 2.3 0.0 0.0 0.0 0.0
OWH TRM MB STHR LHE FTC PINK OBO YR LFB SPW RBTR DWS BELL LWB CBW GGC PIL SKF
Reedy Lake 0.0 15.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.9 0.0 0.0 0.4 0.0 0.0 0.0 0.0 0.0 1.9
Pearcedale 0.0 0.0 0.0 0.0 0.0 2.3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Warneet 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 3.5 0.0 0.0 0.0 0.0 0.0 0.0
Cranbourne 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 5.5 0.0 4.0 0.0 0.0 0.0 0.0
Lysterfield 0.0 0.0 0.0 0.0 0.0 2.1 0.0 1.4 0.0 0.0 0.0 0.0 0.0 22.1 0.0 0.0 0.0 0.0 0.0
Red Hill 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Devilbend 0.0 0.0 3.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.8 0.0 0.0 0.0 0.0 0.0 0.0
Olinda 0.0 0.0 0.0 0.0 0.0 2.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Fern Tree Gum 0.0 0.0 0.0 0.0 0.0 2.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.3 1.3 0.0
Sherwin 0.0 0.0 1.2 0.0 0.0 1.7 0.0 1.2 0.0 0.0 0.0 0.6 0.0 0.0 0.0 0.6 0.0 0.0 2.3
Heathcote Ju 0.0 0.0 0.0 0.9 0.0 1.6 0.0 0.0 0.0 0.0 0.0 1.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Warburton 0.0 0.0 0.0 1.4 2.1 2.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.8 0.7 0.0
Millgrove 0.0 0.0 0.0 0.0 0.0 3.5 0.0 0.0 0.0 0.0 0.0 1.1 0.9 0.0 0.0 0.0 0.0 0.0 0.0
Ben Cairn 3.7 0.0 0.0 0.0 4.1 4.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 3.7 2.8 0.0
Panton Gap 0.6 0.0 0.0 0.9 1.8 3.1 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 4.8 1.8 0.0
OShannassy 0.0 0.0 0.0 0.0 2.4 5.4 2.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.2 0.0
Ghin Ghin 0.0 0.0 0.0 0.0 0.0 2.4 0.0 1.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.8
Minto 2.8 0.0 0.0 0.0 0.0 1.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.7
Hawke 0.0 0.0 0.0 0.0 0.0 1.1 0.0 0.0 0.0 0.0 0.0 1.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0
St Andrews 0.0 0.0 1.7 0.0 0.0 3.4 0.0 0.0 0.0 0.0 0.0 0.0 0.9 15.0 0.0 0.0 0.0 0.0 2.0
Nepean 0.0 0.0 2.2 0.0 0.0 1.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Cape Schanck 0.0 0.0 0.0 0.0 0.0 1.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 32.2 0.0 0.0 0.0 0.0
Balnarring 0.0 0.0 4.9 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 16.5 1.0 0.0 0.0 0.0
Bittern 0.0 0.0 0.0 0.0 0.0 2.3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 5.8 0.0 0.0 0.0 0.0
Bailieston 0.0 0.0 0.0 0.0 0.0 0.0 0.0 3.3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.7 0.0 0.0 0.0
Donna Buang 0.7 0.0 0.0 0.0 2.2 2.2 0.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.7 4.4 0.0
Upper Yarra 0.0 0.0 0.0 0.0 0.9 2.3 0.0 0.0 0.0 0.0 0.0 0.0 0.7 0.0 0.0 0.0 0.0 0.0 1.6
Gembrook 0.0 0.0 0.8 2.4 1.9 2.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Arcadia 0.0 2.5 0.0 0.0 0.0 0.6 0.0 2.5 0.0 1.4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.1
Undera 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 3.2 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.1
Coomboona 0.0 0.6 0.0 0.0 0.0 0.0 0.0 0.0 2.6 5.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.2
Toolamba 0.0 3.3 0.0 0.0 0.0 0.0 0.0 2.0 0.0 6.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0
Rushworth 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.1 0.0 0.0 1.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Sayers 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.6 0.0 0.0 0.0
Waranga 0.0 4.8 0.0 0.0 0.0 0.0 0.0 2.4 0.0 0.0 0.0 0.0 4.8 0.0 0.0 0.0 0.0 0.0 1.4
Costerfield 0.0 0.0 0.0 0.0 0.0 1.6 0.0 1.1 0.0 0.0 3.3 0.0 0.6 0.0 0.0 0.0 0.0 0.0 0.0
Tallarook 0.0 0.0 0.0 0.0 0.0 2.9 0.0 0.0 0.0 0.0 2.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.7
RSL PDOV CRP JW BCHE RCR GBB RRP LLOR YTHE RF SHBC AZKF SFC YRTH ROSE BCOO LFC WG
Reedy Lake 6.7 0.0 0.0 0.0 0.0 0.0 0.0 4.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Pearcedale 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Warneet 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.4 0.0 0.0 0.0 0.0 0.0 1.8 0.0
Cranbourne 0.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Lysterfield 0.0 0.0 0.0 0.0 0.0 0.0 0.7 0.0 0.0 0.0 0.0 0.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Red Hill 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.4 0.0 0.0 3.4 0.0 0.0 0.0 0.0 0.0
Devilbend 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.4 0.0
Olinda 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.9 2.0 0.7 1.2 0.0 0.6 0.0 0.0 0.0
Fern Tree Gum 0.0 0.0 0.0 0.0 0.0 0.0 0.6 0.0 0.0 0.0 3.2 1.3 0.0 1.9 0.0 0.0 0.6 0.0 0.0
Sherwin 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.6 0.0 1.2 0.0 0.0 0.0 0.0 0.0
Heathcote Ju 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.5 0.0 1.6 0.0 0.0 0.0 0.0 0.0
Warburton 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.8 2.1 0.0 4.1 0.0 0.0 0.0 0.0 0.0
Millgrove 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.1 0.0 0.0 7.6 0.0 0.0 0.0 0.0 0.0
Ben Cairn 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 4.6 1.9 0.0 2.8 0.0 1.9 2.8 0.0 0.0
Panton Gap 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.8 3.7 0.0 1.8 0.0 3.1 1.2 0.0 0.0
OShannassy 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.6 1.6 0.0 0.0 0.0 0.7 1.6 0.0 0.0
Ghin Ghin 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.8 0.0 0.0 3.9 0.0 0.0 1.2 0.0
Minto 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Hawke 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
St Andrews 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Nepean 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.2 1.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Cape Schanck 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.6 0.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Balnarring 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Bittern 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Bailieston 0.0 0.0 0.0 0.0 0.0 3.3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Donna Buang 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.2 0.7 0.0 0.7 0.0 1.5 0.0 0.0 0.0
Upper Yarra 0.0 0.0 0.0 0.0 0.0 0.0 0.9 0.0 0.0 0.0 0.0 1.6 0.0 0.8 0.0 0.0 0.0 0.0 0.0
Gembrook 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.8 1.8 0.0 0.0 0.0 0.0 0.0 5.5 0.0
Arcadia 11.0 3.1 1.8 1.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.5 0.0
Undera 0.0 0.0 0.0 3.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.1
Coomboona 1.1 0.0 1.1 2.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.6
Toolamba 5.0 0.4 0.0 0.0 1.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Rushworth 1.4 0.0 0.0 0.0 0.0 0.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5
Sayers 1.7 0.0 0.0 0.0 0.0 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Waranga 0.0 0.8 0.0 0.0 0.0 0.0 0.8 4.8 10.9 2.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Costerfield 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 6.3 0.0 1.6 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Tallarook 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.9 0.0 0.0 0.0 0.0 0.0 0.0 0.0
PCOO WTG NMIN NFB DB RBEE HBC DF PCL FLAME WWT WBWS LCOR KING
Reedy Lake 1.9 0.0 0.2 0.0 0.0 0.0 0.0 0.0 9.1 0.0 0.0 0.0 0.0 0.0
Pearcedale 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Warneet 0.0 0.0 5.8 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Cranbourne 0.0 0.0 3.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Lysterfield 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Red Hill 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Devilbend 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Olinda 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Fern Tree Gum 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Sherwin 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Heathcote Ju 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Warburton 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.8
Millgrove 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Ben Cairn 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Panton Gap 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
OShannassy 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.7
Ghin Ghin 0.0 0.8 0.0 1.8 1.2 0.0 0.0 0.0 0.0 2.6 0.0 0.0 0.0 0.0
Minto 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Hawke 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
St Andrews 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Nepean 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Cape Schanck 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Balnarring 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.9 0.0 0.0 0.0 0.0
Bittern 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Bailieston 0.0 3.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Donna Buang 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 2.9 0.0 0.0 0.0 0.0
Upper Yarra 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Gembrook 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Arcadia 0.0 0.0 0.0 0.0 1.4 1.4 0.0 0.0 0.0 1.8 2.1 0.0 4.8 0.0
Undera 0.0 3.1 0.0 1.5 0.0 1.0 0.0 0.0 0.0 5.9 0.0 0.0 0.0 0.0
Coomboona 0.0 1.6 5.4 0.0 1.6 0.0 0.0 0.0 0.0 1.7 0.0 0.0 0.0 0.0
Toolamba 0.0 0.0 5.7 0.8 1.5 0.5 0.4 0.0 0.0 0.0 2.5 0.0 0.0 0.0
Rushworth 0.0 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Sayers 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
Waranga 0.0 0.0 1.4 2.4 0.0 0.7 0.0 2.1 0.0 0.0 0.0 1.6 0.0 0.0
Costerfield 0.0 0.0 0.0 0.0 0.0 1.1 0.0 1.1 0.0 0.0 0.0 0.0 0.0 0.0
Tallarook 0.0 0.0 0.0 0.0 0.0 0.0 0.0 3.8 0.0 0.0 0.0 0.0 0.0 0.0
- It is highly likely that some species will be more abundant than others - some will be very common and others will be rare.
Furthermore, some sites may have similar compositions yet vastly different total abundances. There might be numereous ecological
explanations for such situations, yet we are primarily interested in describing the community compositions.
- Calculate the means and maximums of each species
Show code
> apply(macnally[, c(-1, -2)], 2, mean, na.rm = TRUE)
EYR GF BTH GWH WTTR WEHE WNHE SFW WBSW CR LK 3.71081 6.11622 14.70270 3.63784 4.50811 3.56216 9.14865 5.98919 5.06757 5.38919 2.90000 RWB AUR STTH LR WPHE YTH ER PCU ESP SCR RBFT 5.67297 2.17297 7.98378 3.41622 7.21351 2.82703 2.25135 0.90000 3.55946 1.08108 3.18108 BFCS WAG WWCH NHHE VS CST BTR AMAG SCC RWH WSW 1.31081 0.94595 2.76757 2.84595 2.04865 0.96486 1.22703 1.12973 6.51081 4.08919 1.99730 STP YFHE WHIP GAL FHE BRTH SPP SIL GCU MUSK MGLK 2.57838 5.12162 0.70541 1.06486 1.91351 2.33784 3.08649 3.03514 0.90270 1.51351 0.40541 BHHE RFC YTBC LYRE CHE OWH TRM MB STHR LHE FTC 2.40541 0.46486 0.73514 0.31351 1.15405 0.21081 0.70811 0.42973 0.15135 0.41622 1.60811 PINK OBO YR LFB SPW RBTR DWS BELL LWB CBW GGC 0.10811 0.45135 0.15676 0.48108 0.19730 0.13514 0.51622 1.00270 1.58108 0.13243 0.33243 PIL SKF RSL PDOV CRP JW BCHE RCR GBB RRP LLOR 0.35676 0.58919 0.74865 0.11622 0.07838 0.21081 0.03243 0.14054 0.09459 0.25946 0.29459 YTHE RF SHBC AZKF SFC YRTH ROSE BCOO LFC WG PCOO 0.24324 0.73514 0.83514 0.01892 0.73243 0.26486 0.21081 0.16757 0.36216 0.14054 0.05135 WTG NMIN NFB DB RBEE HBC DF PCL FLAME WWT WBWS 0.24595 0.58378 0.17568 0.15405 0.12703 0.02432 0.18919 0.24595 0.45405 0.12432 0.04324 LCOR KING 0.12973 0.04054> apply(macnally[, c(-1, -2)], 2, max)
EYR GF BTH GWH WTTR WEHE WNHE SFW WBSW CR LK RWB AUR STTH LR WPHE 9.7 13.3 36.1 9.5 12.8 11.5 38.9 22.0 12.6 19.1 6.7 26.3 8.8 25.2 16.5 27.7 YTH ER PCU ESP SCR RBFT BFCS WAG WWCH NHHE VS CST BTR AMAG SCC RWH 20.2 9.1 3.7 26.6 6.2 44.7 6.9 6.3 11.7 33.3 10.1 4.6 12.5 8.6 80.5 10.9 WSW STP YFHE WHIP GAL FHE BRTH SPP SIL GCU MUSK MGLK BHHE RFC YTBC LYRE 24.3 8.7 26.7 3.8 8.6 26.2 30.6 8.3 17.5 5.7 20.0 3.7 14.1 4.3 5.5 3.0 CHE OWH TRM MB STHR LHE FTC PINK OBO YR LFB SPW RBTR DWS BELL LWB 11.2 3.7 15.0 4.9 2.4 4.1 5.4 2.2 3.3 3.2 6.6 3.3 1.7 5.5 22.1 32.2 CBW GGC PIL SKF RSL PDOV CRP JW BCHE RCR GBB RRP LLOR YTHE RF SHBC 1.7 4.8 4.4 2.3 11.0 3.1 1.8 3.8 1.2 3.3 0.9 4.8 10.9 6.3 4.6 3.7 AZKF SFC YRTH ROSE BCOO LFC WG PCOO WTG NMIN NFB DB RBEE HBC DF PCL 0.7 7.6 5.9 3.1 2.8 5.5 3.1 1.9 3.1 5.8 2.4 1.6 1.4 0.5 3.8 9.1 FLAME WWT WBWS LCOR KING 5.9 2.5 1.6 4.8 0.8
> apply(macnally[, c(-1, -2)], 2, sum)
EYR GF BTH GWH WTTR WEHE WNHE SFW WBSW CR LK RWB AUR STTH LR WPHE 137.3 226.3 544.0 134.6 166.8 131.8 338.5 221.6 187.5 199.4 107.3 209.9 80.4 295.4 126.4 266.9 YTH ER PCU ESP SCR RBFT BFCS WAG WWCH NHHE VS CST BTR AMAG SCC RWH 104.6 83.3 33.3 131.7 40.0 117.7 48.5 35.0 102.4 105.3 75.8 35.7 45.4 41.8 240.9 151.3 WSW STP YFHE WHIP GAL FHE BRTH SPP SIL GCU MUSK MGLK BHHE RFC YTBC LYRE 73.9 95.4 189.5 26.1 39.4 70.8 86.5 114.2 112.3 33.4 56.0 15.0 89.0 17.2 27.2 11.6 CHE OWH TRM MB STHR LHE FTC PINK OBO YR LFB SPW RBTR DWS BELL LWB 42.7 7.8 26.2 15.9 5.6 15.4 59.5 4.0 16.7 5.8 17.8 7.3 5.0 19.1 37.1 58.5 CBW GGC PIL SKF RSL PDOV CRP JW BCHE RCR GBB RRP LLOR YTHE RF SHBC 4.9 12.3 13.2 21.8 27.7 4.3 2.9 7.8 1.2 5.2 3.5 9.6 10.9 9.0 27.2 30.9 AZKF SFC YRTH ROSE BCOO LFC WG PCOO WTG NMIN NFB DB RBEE HBC DF PCL 0.7 27.1 9.8 7.8 6.2 13.4 5.2 1.9 9.1 21.6 6.5 5.7 4.7 0.9 7.0 9.1 FLAME WWT WBWS LCOR KING 16.8 4.6 1.6 4.8 1.5
> apply(macnally[, c(-1, -2)], 2, var, na.rm = TRUE)
EYR GF BTH GWH WTTR WEHE WNHE SFW WBSW CR 7.71988 17.85306 124.66083 7.38686 10.16465 10.08520 74.11923 25.76432 17.33892 29.98488 LK RWB AUR STTH LR WPHE YTH ER PCU ESP 2.40556 53.48480 3.45592 42.44806 16.91695 114.58953 27.02036 5.44090 1.62944 22.94581 SCR RBFT BFCS WAG WWCH NHHE VS CST BTR AMAG 3.53102 58.37213 1.72766 2.73811 15.70670 56.29366 7.71590 1.53734 8.01592 5.89381 SCC RWH WSW STP YFHE WHIP GAL FHE BRTH SPP 277.33266 10.75321 22.84805 6.97841 43.93785 1.79219 5.68068 31.27842 36.39131 4.84565 SIL GCU MUSK MGLK BHHE RFC YTBC LYRE CHE OWH 16.06790 1.95360 21.30287 0.83775 14.60164 1.12012 2.00623 0.54731 6.75089 0.57599 TRM MB STHR LHE FTC PINK OBO YR LFB SPW 6.86077 1.14437 0.23590 0.91862 2.03021 0.16799 0.74646 0.44697 2.25491 0.52971 RBTR DWS BELL LWB CBW GGC PIL SKF RSL PDOV 0.17623 1.70973 18.78360 35.17324 0.17114 1.05725 0.90974 0.78488 4.91257 0.27529 CRP JW BCHE RCR GBB RRP LLOR YTHE RF SHBC 0.11730 0.61321 0.03892 0.31859 0.06164 1.21081 3.21108 1.24419 1.43068 0.91512 AZKF SFC YRTH ROSE BCOO LFC WG PCOO WTG NMIN 0.01324 2.43170 1.31734 0.40766 0.31003 1.16908 0.32470 0.09757 0.56755 2.61917 NFB DB RBEE HBC DF PCL FLAME WWT WBWS LCOR 0.29856 0.20366 0.11980 0.01078 0.52044 2.23811 1.44700 0.28023 0.06919 0.62270 KING 0.02970 - Perform this standardization on the bird abundance data and confirm that this has evened out the abundances
Show code
> library(vegan) > macnally.std <- wisconsin(macnally[, c(-1, -2)]) > apply(macnally.std[, c(-1, -2)], 2, max)
BTH GWH WTTR WEHE WNHE SFW WBSW CR LK RWB AUR STTH 0.06781 0.07385 0.08452 0.07973 0.05925 0.07502 0.14357 0.07300 0.09260 0.08625 0.07300 0.06173 LR WPHE YTH ER PCU ESP SCR RBFT BFCS WAG WWCH NHHE 0.08024 0.14305 0.10025 0.08024 0.06672 0.04966 0.07914 0.05685 0.05846 0.07973 0.08486 0.09702 VS CST BTR AMAG SCC RWH WSW STP YFHE WHIP GAL FHE 0.08024 0.08412 0.06491 0.06491 0.05302 0.07101 0.08459 0.06218 0.05823 0.07076 0.05855 0.06491 BRTH SPP SIL GCU MUSK MGLK BHHE RFC YTBC LYRE CHE OWH 0.06817 0.06885 0.05302 0.05610 0.06900 0.04788 0.07914 0.04788 0.04966 0.07267 0.04966 0.04963 TRM MB STHR LHE FTC PINK OBO YR LFB SPW RBTR DWS 0.06491 0.08024 0.04966 0.04963 0.06217 0.06217 0.07914 0.05855 0.06309 0.06011 0.10713 0.09126 BELL LWB CBW GGC PIL SKF RSL PDOV CRP JW BCHE RCR 0.07300 0.09702 0.09435 0.05566 0.07267 0.08512 0.04788 0.04788 0.04788 0.05855 0.06309 0.07914 GBB RRP LLOR YTHE RF SHBC AZKF SFC YRTH ROSE BCOO LFC 0.08452 0.06491 0.04603 0.06011 0.05484 0.05566 0.08505 0.06123 0.05855 0.05566 0.04963 0.04966 WG PCOO WTG NMIN NFB DB RBEE HBC DF PCL FLAME WWT 0.05855 0.06491 0.07914 0.08459 0.04603 0.05915 0.04788 0.08625 0.06817 0.06491 0.05855 0.06309 WBWS LCOR KING 0.04603 0.04788 0.05440> apply(macnally.std[, c(-1, -2)], 2, var, na.rm = TRUE)
BTH GWH WTTR WEHE WNHE SFW WBSW CR LK RWB 4.704e-04 3.970e-04 3.743e-04 5.246e-04 2.256e-04 3.121e-04 1.070e-03 3.795e-04 3.270e-04 5.362e-04 AUR STTH LR WPHE YTH ER PCU ESP SCR RBFT 2.258e-04 3.030e-04 3.448e-04 1.088e-03 4.462e-04 4.023e-04 5.698e-04 1.020e-04 4.593e-04 9.532e-05 BFCS WAG WWCH NHHE VS CST BTR AMAG SCC RWH 1.590e-04 4.435e-04 6.529e-04 4.579e-04 4.017e-04 3.738e-04 1.879e-04 2.768e-04 1.293e-04 4.836e-04 WSW STP YFHE WHIP GAL FHE BRTH SPP SIL GCU 2.857e-04 3.781e-04 2.499e-04 4.947e-04 2.709e-04 1.819e-04 2.000e-04 3.802e-04 1.871e-04 2.461e-04 MUSK MGLK BHHE RFC YTBC LYRE CHE OWH TRM MB 2.261e-04 2.003e-04 4.002e-04 1.642e-04 2.324e-04 3.176e-04 2.172e-04 1.111e-04 1.222e-04 3.187e-04 STHR LHE FTC PINK OBO YR LFB SPW RBTR DWS 1.197e-04 1.715e-04 3.327e-04 1.348e-04 3.043e-04 1.495e-04 1.942e-04 2.064e-04 5.152e-04 3.397e-04 BELL LWB CBW GGC PIL SKF RSL PDOV CRP JW 1.934e-04 2.976e-04 4.610e-04 1.362e-04 2.051e-04 6.308e-04 1.241e-04 6.597e-05 9.389e-05 1.429e-04 BCHE RCR GBB RRP LLOR YTHE RF SHBC AZKF SFC 1.076e-04 1.860e-04 4.313e-04 1.666e-04 5.725e-05 1.064e-04 3.168e-04 3.014e-04 1.955e-04 1.755e-04 YRTH ROSE BCOO LFC WG PCOO WTG NMIN NFB DB 1.275e-04 1.418e-04 1.150e-04 1.282e-04 1.180e-04 1.139e-04 2.769e-04 4.055e-04 1.428e-04 2.607e-04 RBEE HBC DF PCL FLAME WWT WBWS LCOR KING 1.780e-04 2.634e-04 1.462e-04 1.139e-04 1.570e-04 1.475e-04 5.725e-05 6.195e-05 1.443e-04 - We now need to generate a distance matrix reflecting the multidimensional distance between each of the site pairs.
The Bray-Curtis dissimilarity index is a very popular distance metric as it:
- Reaches a maximum of 1 when two sites have nothing in common
- Reaches a minimum of 0 when two sites are identical
- Ignores shared absences, so dissimilarity is based only on the values of characteristics that the objects do share - two sites are not considered similar just because they both do not contain a certain species.
Show code> macnally.dist <- vegdist(macnally.std, "bray")
- Perform a non-metric multidimensional scaling with:
- two dimensions ($k=2$)
- use principle coordinates analysis to create the initial configuration
- use a maximum of 20 random starts
- use (modified) Kruskal's stress to determine the match between ordination distances and ecological distances
- use procrustes rotation to determine whether the configurations have converged
- center the axes scores and rotate the points such that the greatest plane of variation is orientated with the primary axis
Show code> macnally.mds <- metaMDS(macnally.dist, k = 2)Run 0 stress 0.1239 Run 1 stress 0.1239 ... New best solution ... procrustes: rmse 0.003365 max resid 0.01766 Run 2 stress 0.1716 Run 3 stress 0.1368 Run 4 stress 0.1368 Run 5 stress 0.1862 Run 6 stress 0.1239 ... procrustes: rmse 0.0003442 max resid 0.001192 *** Solution reached
- What is the final stress value?
Show code
> macnally.mds$stress
[1] 0.1239
- What does this stress value suggest about the success of the MDS, are two dimensions adequate?
- The Sheppard diagram (stress plot) represents the relationship between the ecological distances (y-axis) and the new MDS ordination distances (x-axis).
How would you describe the shape of this curve, and base on this is metric or non-metric MDS more appropriate?
Show code> stressplot(macnally.mds)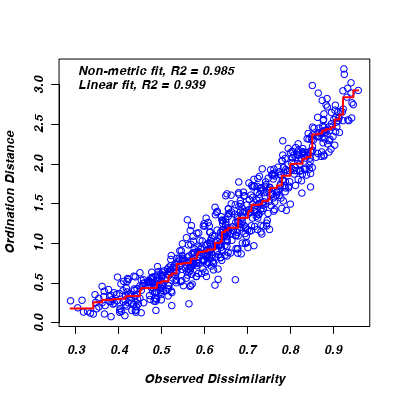
-
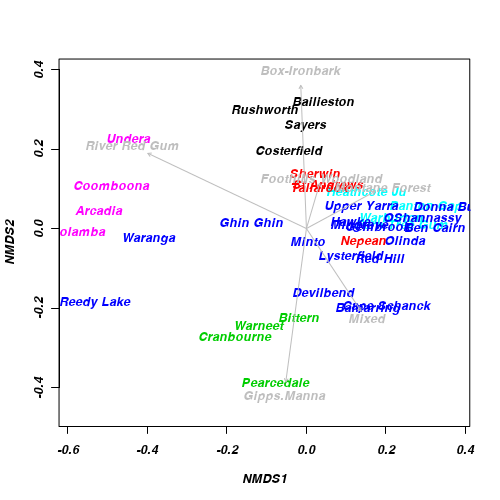
Generate an ordination plot to represent the similarity of the bird communities of the sites graphically.
Show code
> ordiplot(macnally.mds, display = "sites", type = "n") > text(macnally.mds, lab = rownames(macnally), col = as.numeric(macnally$HABITAT)) > habitat <- model.matrix(~-1 + macnally$HABITAT) > colnames(habitat) <- gsub("macnally\\$HABITAT", "", colnames(habitat)) > envfit <- envfit(macnally.mds, env = habitat) > envfit
***VECTORS NMDS1 NMDS2 r2 Pr(>r) Box-Ironbark -0.0395 0.9992 0.35 0.002 ** Foothills Woodland 0.2828 0.9592 0.04 0.496 Gipps.Manna -0.1333 -0.9911 0.41 0.001 *** Mixed 0.5517 -0.8341 0.17 0.037 * Montane Forest 0.8796 0.4756 0.10 0.149 River Red Gum -0.9036 0.4284 0.53 0.001 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 P values based on 999 permutations.> plot(envfit, col = "gray")
The nature of mathematics is that large numbers yield larger and more disparate values than smaller values. Hence in order to describe the communities in a way that all species and sites have an equal opportunity to influence the patterns, we should first standardize the species abundances.
There are a number of valid standardizations that we could attempt (and indeed you are encouraged to try a couple of alternatives to the one we use here). One popular and suitable standardization for ecological species abundance data is the Wisconsin double standardization. Not only does this standardization help suppress the dominance of the overly abundant species, it also magnifies the main patterns thereby making them easier to detect.
- Calculate the means and maximums of each species
